Article contents
The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects
Published online by Cambridge University Press: 11 May 2016
Abstract
In Part 1 of this study (Ireland et al., J. Fluid Mech., vol. 796, 2016, pp. 617–658), we analysed the motion of inertial particles in isotropic turbulence in the absence of gravity using direct numerical simulation (DNS). Here, in Part 2, we introduce gravity and study its effect on single-particle and particle-pair dynamics over a wide range of flow Reynolds numbers, Froude numbers and particle Stokes numbers. The overall goal of this study is to explore the mechanisms affecting particle collisions, and to thereby improve our understanding of droplet interactions in atmospheric clouds. We find that the dynamics of heavy particles falling under gravity can be artificially influenced by the finite domain size and the periodic boundary conditions, and we therefore perform our simulations on larger domains to reduce these effects. We first study single-particle statistics that influence the relative positions and velocities of inertial particles. We see that gravity causes particles to sample the flow more uniformly and reduces the time particles can spend interacting with the underlying turbulence. We also find that gravity tends to increase inertial particle accelerations, and we introduce a model to explain that effect. We then analyse the particle relative velocities and radial distribution functions (RDFs), which are generally seen to be independent of Reynolds number for low and moderate Kolmogorov-scale Stokes numbers 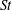 $St$. We see that gravity causes particle relative velocities to decrease by reducing the degree of preferential sampling and the importance of path-history interactions, and that the relative velocities have higher scaling exponents with gravity. We observe that gravity has a non-trivial effect on clustering, acting to decrease clustering at low
$St$. We see that gravity causes particle relative velocities to decrease by reducing the degree of preferential sampling and the importance of path-history interactions, and that the relative velocities have higher scaling exponents with gravity. We observe that gravity has a non-trivial effect on clustering, acting to decrease clustering at low 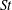 $St$ and to increase clustering at high
$St$ and to increase clustering at high 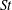 $St$. By considering the effect of gravity on the clustering mechanisms described in the theory of Zaichik & Alipchenkov (New J. Phys., vol. 11, 2009, 103018), we provide an explanation for this non-trivial effect of gravity. We also show that when the effects of gravity are accounted for in the theory of Zaichik & Alipchenkov (2009), the results compare favourably with DNS. The relative velocities and RDFs exhibit considerable anisotropy at small separations, and this anisotropy is quantified using spherical harmonic functions. We use the relative velocities and the RDFs to compute the particle collision kernels, and find that the collision kernel remains as it was for the case without gravity, namely nearly independent of Reynolds number for low and moderate
$St$. By considering the effect of gravity on the clustering mechanisms described in the theory of Zaichik & Alipchenkov (New J. Phys., vol. 11, 2009, 103018), we provide an explanation for this non-trivial effect of gravity. We also show that when the effects of gravity are accounted for in the theory of Zaichik & Alipchenkov (2009), the results compare favourably with DNS. The relative velocities and RDFs exhibit considerable anisotropy at small separations, and this anisotropy is quantified using spherical harmonic functions. We use the relative velocities and the RDFs to compute the particle collision kernels, and find that the collision kernel remains as it was for the case without gravity, namely nearly independent of Reynolds number for low and moderate 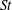 $St$. We conclude by discussing practical implications of the results for the cloud physics and turbulence communities and by suggesting possible avenues for future research.
$St$. We conclude by discussing practical implications of the results for the cloud physics and turbulence communities and by suggesting possible avenues for future research.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
Footnotes
Present address: Applied Mathematics and Plasma Physics Group, Los Alamos National Laboratory, Los Alamos, NM 87545, USA.
References
- 94
- Cited by



