Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T11:26:17.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of isolated roughness element height on high-speed laminar–turbulent transition

Published online by Cambridge University Press:  04 April 2017

David Estruch-Samper Open the ORCID record for David Estruch-Samper [Opens in a new window] ,
Richard Hillier ,
Leon Vanstone  and
Bharathram Ganapathisubramani
David Estruch-Samper*
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575, Singapore
Richard Hillier
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
Leon Vanstone
Affiliation:
Department of Aerospace Engineering, University of Texas at Austin, TX 78712, USA
Bharathram Ganapathisubramani
Affiliation:
Engineering and the Environment, Southampton University, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Understanding of the roughness-induced laminar–turbulent transition of supersonic and hypersonic flows is partly challenged by the intricate sensitivities presented by different correlation criteria. We investigate experimentally the effect of height for an isolated roughness element of quadrilateral planform. Heat transfer measurements document the enhancement of roughness-induced disturbances – here the associated heat flux perturbation – along a downstream axisymmetric laminar separation. With increasing element height 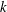$k$, a gradual intensification in wake disturbance levels is found for subcritical elements (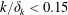$k/\unicode[STIX]{x1D6FF}_{k}<0.15$, where 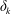$\unicode[STIX]{x1D6FF}_{k}$ is the undisturbed boundary layer thickness) while elements taller than the effective condition (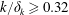$k/\unicode[STIX]{x1D6FF}_{k}\geqslant 0.32$) bypass the more moderate transition mechanisms to produce a fully turbulent element wake. Results exhibit high sensitivity to flow properties at roughness height between critical and effective conditions. A reduction in wake disturbance levels with increasing height is documented within 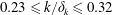$0.23\leqslant k/\unicode[STIX]{x1D6FF}_{k}\leqslant 0.32$. This effect coincides with a decrease in kinematic viscosity at roughness height 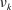$\unicode[STIX]{x1D708}_{k}$ (as Mach number at height 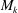$M_{k}$ increases from 1.52 to 1.96) and is restricted to elements with strong local separation, whereby the influence of local shear effects is enhanced.

JFM classification

Compressible Flows: Compressible boundary layers Aerodynamics: High-speed flow Instability: Transition to turbulence
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bernardini, M., Pirozzoli, S. & Orlandi, P. 2012 Compressibility effects on roughness-induced boundary layer transition. Intl J. Heat Fluid Flow 35, 45–51.CrossRefGoogle Scholar
Berry, S. A. & Horvath, T. J. 2008 Discrete roughness transition for hypersonic flight vehicles. J. Spacecr. Rockets 45 (2), 216–227.Google Scholar
Choudhari, M., LI, F., Chang, C.-L. & Edwards, J.2009 On the effects of surface roughness on boundary-layer transition. NASA Rep. LF99-8476.Google Scholar
Choudhari, M., Li, F., Chang, C.-L., Norris, A. & Edwards, J.2013 Wake instabilities behind discrete roughness elements in high speed boundary layers. AIAA Paper 2013-0081.Google Scholar
Choudhari, M., Li, F., Wu, M., Chang, C.-L., Edwards, J., Kegerise, M. & King, R.2010 Laminar-turbulent transition behind discrete roughness elements in a high-speed boundary layer. AIAA Paper 2010-1575.Google Scholar
De Tullio, N., Paredes, P., Sandham, N. D. & Theofilis, V. 2013 Laminar-turbulent transition induced by a discrete roughness element in a supersonic boundary layer. J. Fluid Mech. 735, 613–646.Google Scholar
De Tullio, N. & Sandham, N. D. 2015 Influence of boundary-layer disturbances on instability of a roughness wake in a high-speed boundary layer. J. Fluid Mech. 763, 136–165.CrossRefGoogle Scholar
Estruch-Samper, D. 2016 Reattachment heating upstream of short compression ramps in hypersonic flow. Exp. Fluids 57 (5), 1–17.CrossRefGoogle Scholar
Fedorov, A. 2011 Transition and stability of high-speed boundary-layers. Annu. Rev. Fluid Mech. 44, 79–95.Google Scholar
Fiala, A., Hillier, R. & Estruch-Samper, D. 2014 Roughness-induced turbulent wedges in a hypersonic blunt-body boundary layer. J. Fluid Mech. 754, 208–231.CrossRefGoogle Scholar
Fiala, A., Hillier, R., Mallinson, S. G. & Wijensinghe, H. S. 2006 Heat transfer measurement of turbulent spots in a hypersonic blunt-body boundary layer. J. Fluid Mech. 555, 81–111.CrossRefGoogle Scholar
Horvath, T. J., Zalameda, J. N., Wood, W. A., Berry, S. A., Schwartz, R. J., Dantowitz, R. F., Spisz, T. S. & Taylor, J. C.2012 Global infrared observations of roughness induced transition on the Space Shuttle Orbiter. NATO RTO-MP-ABT-200, Art. 27.Google Scholar
Iyer, P. S. & Mahesh, K. 2013 High-speed boundary-layer transition induced by a discrete roughness element. J. Fluid Mech. 729, 524–562.CrossRefGoogle Scholar
Kegerise, M., King, R., Owens, L., Choudhari, M., Norris, A., Li, F. & Chang, C.-L.2012 An experimental and numerical study of roughness-induced instabilities in a Mach 3.5 boundary layer. NASA Rep. 2012-0007198.Google Scholar
Reda, D. C. 2002 Review and synthesis of roughness-dominated transition correlations for reentry applications. J. Spacecr. Rockets 39 (2), 161–167.CrossRefGoogle Scholar
Reshotko, E. 2007 Is Re 𝜃/M e a meaningful transition criterion? AIAA J. 45 (7), 1441–1443.Google Scholar
Reshotko, E. & Tumin, A. 2004 Role of transient growth in roughness-induced transition. AIAA J. 42 (4), 766–770.Google Scholar
Schneider, S. P. 2008 Effects of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45 (2), 193–209.Google Scholar
Subbareddy, P., Bartkowicz, M. & Candler, G. 2014 Direct numerical simulation of high-speed transition due to an isolated roughness element. J. Fluid Mech. 748, 848–878.CrossRefGoogle Scholar