Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T03:31:47.311Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of Dean, Reynolds and Womersley numbers on the flow in a spherical cavity on a curved round pipe. Part 1. Fluid mechanics in the cavity as a canonical flow representing intracranial aneurysms

Published online by Cambridge University Press:  31 March 2021

Fanette Chassagne Open the ORCID record for Fanette Chassagne [Opens in a new window] ,
Michael C. Barbour Open the ORCID record for Michael C. Barbour [Opens in a new window] ,
Venkat K. Chivukula Open the ORCID record for Venkat K. Chivukula [Opens in a new window] ,
Nathanael Machicoane Open the ORCID record for Nathanael Machicoane [Opens in a new window] ,
Louis J. Kim Open the ORCID record for Louis J. Kim [Opens in a new window] ,
Michael R. Levitt Open the ORCID record for Michael R. Levitt [Opens in a new window]  and
Alberto Aliseda Open the ORCID record for Alberto Aliseda [Opens in a new window]
Fanette Chassagne*
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA98105, USA
Michael C. Barbour
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA98105, USA
Venkat K. Chivukula
Affiliation:
Biomedical and Chemical Engineering and Sciences, Florida Institute of Technology, Melbourne, FL32901, USA
Nathanael Machicoane
Affiliation:
University Grenoble Alpes, CNRS, Grenoble-INP, LEGI, 38000Grenoble, France
Louis J. Kim
Affiliation:
Department of Neurological Surgery, University of Washington, Seattle, WA98107, USA Department of Radiology, University of Washington, Seattle, WA98107, USA
Michael R. Levitt
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA98105, USA Department of Neurological Surgery, University of Washington, Seattle, WA98107, USA Department of Radiology, University of Washington, Seattle, WA98107, USA
Alberto Aliseda
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA98105, USA Department of Neurological Surgery, University of Washington, Seattle, WA98107, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

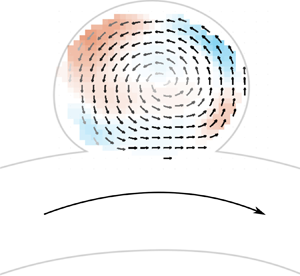
Flow in sidewall cerebral aneurysms can be ideally modelled as the combination of flow over a spherical cavity and flow in a curved circular pipe, two canonical flows. Flow in a curved pipe is known to depend on the Dean number $De$, combining the effects of Reynolds number $\textit {Re}$ and of the curvature along the pipe centreline, $\kappa$. Pulsatility in the flow introduces a dependence on the Womersley number $Wo$. Using stereo particle image velocimetry measurements, this study investigated the effect of these three key non-dimensional parameters, by modifying pipe curvature ($De$), flow rate ($Re$) and pulsatility frequency ($Wo$), on the flow patterns in a spherical cavity. A single counter-rotating vortex was observed in the cavity for all values of pipe curvature $\kappa$ and Reynolds number $\textit {Re}$, for both steady and pulsatile inflow conditions. Increasing the pipe curvature impacted the flow patterns in both the pipe and the cavity, by shifting the velocity profile towards the cavity opening and increasing the flow rate in to the cavity. The circulation in the cavity was found to collapse well with only the Dean number, for both steady and pulsatile inflows. For pulsatile inflow, the counter-rotating vortex was unstable and the location of its centre over time was impacted by the curvature of the pipe, as well as $\textit {Re}$ and $Wo$ in the free stream. The circulation in the cavity was higher for steady inflow than for the equivalent average Reynolds number and Dean number pulsatile inflow, with very limited impact of the Womersley number in the range studied. A second part of this study, that focuses on the changes in fluid dynamics when the intracranial aneurysm is treated with a flow-diverting stent, can be found in this issue (Barbour et al., J. Fluid Mech., vol. 915, 2021, A124).

JFM classification

Biological Fluid Dynamics: Biomedical flows Biological Fluid Dynamics: Blood flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A123
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Asgharzadeh, H., Asadi, H., Meng, H. & Borazjani, I. 2019 A non-dimensional parameter for classification of the flow in intracranial aneurysms. II. Patient-specific geometries. Phys. Fluids 31 (3), 031905.CrossRefGoogle ScholarPubMed
Asgharzadeh, H. & Borazjani, I. 2016 Effects of Reynolds and Womersley numbers on the hemodynamics of intracranial aneurysms. Comput. Math. Meth. Med. 2016, 1–16.CrossRefGoogle ScholarPubMed
Barbour, M.C., Chassagne, F., Chivukula, V.K., Machicoane, N., Kim, L.J., Levitt, M.R. & Aliseda, A. 2021 The effect of Dean, Reynolds and Womersley numbers on the flow in a spherical cavity on a curved round pipe. Part 2. The haemodynamics of intracranial aneurysms treated with flow-diverting stents. J. Fluid Mech. 915, A124.Google Scholar
Burggraf, O.R. 1966 Analytical and numerical studies of the structure of steady separated flows. J. Fluid Mech. 24 (1), 113–151.CrossRefGoogle Scholar
Chen, J., Zhang, Y., Tian, Z., Li, W., Zhang, Q., Zhang, Y., Liu, J. & Yang, X. 2019 Relationship between haemodynamic changes and outcomes of intracranial aneurysms after implantation of the pipeline embolisation device: a single centre study. Interv. Neuroradiol. 25 (6), 671–680.CrossRefGoogle ScholarPubMed
Chivukula, V.K., et al. 2019 Reconstructing patient-specific cerebral aneurysm vasculature for in vitro investigations and treatment efficacy assessments. J. Clin. Neurosci. 61, 153–159.CrossRefGoogle ScholarPubMed
Collins, W.M. & Dennis, S.C.R. 1975 The steady motion of a viscous fluid in a curved tube. Q. J. Mech. Appl. Maths 28 (2), 133–156.CrossRefGoogle Scholar
Dean, W.R. 1927 Note on the motion of fluid in a curved pipe. Lond. Edinb. Dubl. Phil. Mag. J. Sci. 4 (20), 208–223.CrossRefGoogle Scholar
Dean, W.R. 1928 The streamline motion of a fluid in a curved pipe. Lond. Edinb. Dubl. Phil. Mag. J. Sci. 5, 673–693.CrossRefGoogle Scholar
Epshtein, M. & Korin, N. 2018 Mapping the transport kinetics of molecules and particles in idealized intracranial side aneurysms. Sci. Rep. 8 (1), 8528.CrossRefGoogle ScholarPubMed
Eustice, J. 1910 Flow of water in curved pipes. Proc. R. Soc. A 84 (568), 107–118.Google Scholar
Eustice, J. 1911 Experiments on stream-line motion in curved pipes. Proc. R. Soc. A 85 (576), 119–131.Google Scholar
Ford, M.D., Alperin, N., Lee, S.H., Holdsworth, D.W. & Steinman, D.A. 2005 Characterization of volumetric flow rate waveforms in the normal internal carotid and vertebral arteries. Physiol. Meas. 26 (4), 477–488.CrossRefGoogle ScholarPubMed
Fukuda, S., et al. 2019 Review on the formation and growth of cerebral aneurysms. J. Biorheol. 33 (2), 43–52.CrossRefGoogle Scholar
Hamakiotes, C.C. & Berger, S.A. 1988 Fully developed pulsatile flow in a curved pipe. J. Fluid Mech. 195, 23–55.CrossRefGoogle Scholar
Higdon, J.J.L. 1985 Stokes flow in arbitrary two-dimensional domains: shear flow over ridges and cavities. J. Fluid Mech. 159, 195–226.CrossRefGoogle Scholar
Hoi, Y., Meng, H., Woodward, S.H., Bendok, B.R., Hanel, R.A., Guterman, L.R. & Hopkins, L.N. 2004 Effects of arterial geometry on aneurysm growth: three-dimensional computational fluid dynamics study. J. Neurosurg. 101 (4), 676–681.CrossRefGoogle ScholarPubMed
Imai, Y., Sato, K., Ishikawa, T. & Yamaguchi, T. 2008 Inflow into saccular cerebral aneurysms at arterial bends. Ann. Biomed. Engng 36 (9), 1489–1495.CrossRefGoogle ScholarPubMed
Le, T.B., Borazjani, I. & Sotiropoulos, F. 2010 Pulsatile flow effects on the hemodynamics of intracranial aneurysms. Trans. ASME J. Biomech. Engng 132 (11), 111009.CrossRefGoogle ScholarPubMed
McConalogue, D.J. & Srivastava, R.S. 1968 Motion of a fluid in a curved tube. Proc. R. Soc. Lond. A 307 (1488), 37–53.Google Scholar
Meng, H., Tutino, V.M., Xiang, J. & Siddiqui, A. 2014 High WSS or low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: toward a unifying hypothesis. Am. J. Neuroradiol. 35 (7), 1254–1262.CrossRefGoogle ScholarPubMed
Nair, P., et al. 2016 Hemodynamic characterization of geometric cerebral aneurysm templates. J. Biomech. 49 (11), 2118–2126.CrossRefGoogle ScholarPubMed
Ngoepe, M.N., Frangi, A.F., Byrne, J.V. & Ventikos, Y. 2018 Thrombosis in cerebral aneurysms and the computational modeling thereof: a review. Front. Physiol. 9, 306.CrossRefGoogle ScholarPubMed
Pan, F. & Acrivos, A. 1967 Steady flows in rectangular cavities. J. Fluid Mech. 28 (4), 643–655.CrossRefGoogle Scholar
Parlea, L., Fahrig, R., Holdsworth, D.W. & Lownie, S.P. 1999 An analysis of the geometry of saccular intracranial aneurysms. AJNR Am. J. Neuroradiol. 20 (6), 1079–1089.Google ScholarPubMed
Rajah, G., Narayanan, S. & Rangel-Castilla, L. 2017 Update on flow diverters for the endovascular management of cerebral aneurysms. Neurosurg. Focus 42 (6), E2.Google ScholarPubMed
Sarno, R.L. & Franke, M.E. 1994 Suppression of flow-induced pressure oscillations in cavities. J. Aircr. 31 (1), 90–96.CrossRefGoogle Scholar
Sforza, D.M., Putman, C.M. & Cebral, J.R. 2009 Hemodynamics of cerebral aneurysms. Annu. Rev. Fluid Mech. 41 (1), 91–107.CrossRefGoogle ScholarPubMed
Shen, C. & Floryan, J.M. 1985 Low Reynolds number flow over cavities. Phys. Fluids 28 (11), 3191.CrossRefGoogle Scholar
Sobey, I.J. 1980 On flow through furrowed channels. Part 1. Calculated flow patterns. J. Fluid Mech. 96 (1), 1–26.CrossRefGoogle Scholar
Stephanoff, K.D., Sobey, I.J. & Bellhouse, B.J. 1980 On flow through furrowed channels. Part 2. Observed flow patterns. J. Fluid Mech. 96 (1), 27–32.CrossRefGoogle Scholar
Su, T., Reymond, P., Brina, O., Bouillot, P., Machi, P., Delattre, B.M.A., Jin, L., Lövblad, K.O. & Vargas, M.I. 2020 Large neck and strong ostium inflow as the potential causes for delayed occlusion of unruptured sidewall intracranial aneurysms treated by flow diverter. Am. J. Neuroradiol. 41 (3), 488–494.CrossRefGoogle ScholarPubMed
Texakalidis, P., Sweid, A., Mouchtouris, N., Peterson, E.C., Sioka, C., Rangel-Castilla, L., Reavey-Cantwell, J. & Jabbour, P. 2019 Aneurysm formation, growth, and rupture: the biology and physics of cerebral aneurysms. World Neurosurg. 130, 277–284.CrossRefGoogle ScholarPubMed
Tippe, A. & Tsuda, A. 2000 Recirculating flow in an expanding alveolar model: experimental evidence of flow-induced mixing of aerosols in the pulmonary acinus. J. Aerosol Sci. 31 (8), 979–986.CrossRefGoogle Scholar
Wan, H., Ge, L., Huang, L., Jiang, Y., Leng, X., Feng, X., Xiang, J. & Zhang, X. 2019 Sidewall aneurysm geometry as a predictor of rupture risk due to associated abnormal hemodynamics. Front. Neurol. 10, 841.CrossRefGoogle ScholarPubMed
Weiss, R.F. & Florsheim, B.H. 1965 Flow in a cavity at low Reynolds number. Phys. Fluids 8 (9), 1631.CrossRefGoogle Scholar
Williams, G.S., Hubbell, C.W. & Fenkell, G.M. 1902 Experiments at Detroit, Mich., on the effect of curvature upon the flow of water in pipes. Trans. Am. Soc. Civil Engrs 47, 1–196.CrossRefGoogle Scholar
Womersley, J.R. 1955 Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. (Lond.) 127 (3), 553–563.CrossRefGoogle ScholarPubMed