Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T18:53:55.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection

Published online by Cambridge University Press:  01 February 2013

Yi-Chao Xie ,
Ping Wei  and
Ke-Qing Xia
Yi-Chao Xie
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ping Wei
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

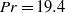We report experimental investigations of the dynamics of the large-scale circulation (LSC) in turbulent Rayleigh–Bénard convection at high Prandtl number $\mathit{Pr}= 19. 4$ (and also 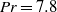$\mathit{Pr}= 7. 8$) and Rayleigh number 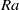$\mathit{Ra}$ varying from 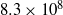$8. 3\times 1{0}^{8} $ to 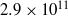$2. 9\times 1{0}^{11} $ in a cylindrical convection cell with aspect ratio unity. The dynamics of the LSC is measured using the multithermal probe technique. Both the sinusoidal-fitting (SF) and the temperature-extrema-extraction (TEE) methods are used to analyse the properties of the LSC. It is found that the LSC in high-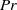$\mathit{Pr}$ regime remains a single-roll structure. The azimuthal motion of the LSC is a diffusive process, which is the same as those for 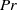$\mathit{Pr}$ around 1. However, the azimuthal diffusion of the LSC, characterized by the angular speed 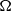$\Omega $ is almost two orders of magnitude smaller when compared with that in water. The non-dimensional time-averaged amplitude of the angular speed 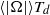$\langle \vert \Omega \vert \rangle {T}_{d} $ (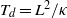${T}_{d} = {L}^{2} / \kappa $ is the thermal diffusion time) of the LSC at the mid-height of the convection cell increases with 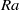$\mathit{Ra}$ as a power law, which is 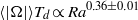$\langle \vert \Omega \vert \rangle {T}_{d} \propto {\mathit{Ra}}^{0. 36\pm 0. 01} $. The 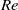$\mathit{Re}$ number based on the oscillation frequency of the LSC is found to scale with 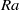$\mathit{Ra}$ as 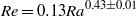$\mathit{Re}= 0. 13{\mathit{Ra}}^{0. 43\pm 0. 01} $. It is also found that the normalized flow strength 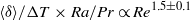$\langle \delta \rangle / \mrm{\Delta} T\times \mathit{Ra}/ \mathit{Pr}\propto {\mathit{Re}}^{1. 5\pm 0. 1} $, with the exponent in good agreement with that predicted by Brown & Ahlers (Phys. Fluids, vol. 20, 2008, p. 075101). A wealth of dynamical features of the LSC, such as the cessations, flow reversals, flow mode transitions, torsional and sloshing oscillations are observed in the high-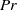$\mathit{Pr}$ regime as well.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 322 - 346
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D. & Hogg, J. 2009a Turbulent Rayleigh–Bénard convection for a Prandtl number of 0.67. J. Fluid Mech. 641, 157–167.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009b Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Ashkenazi, S. & Steinberg, V. 1999 High Rayleigh number turbulent convection in a gas near the gas–liquid critical point. Phys. Rev. Lett. 83, 3641–3644.Google Scholar
Benzi, R. 2005 Flow reversal in a simple dynamical model of turbulence. Phys. Rev. Lett. 95, 024502.Google Scholar
Brown, E. & Ahlers, G. 2006a Effect of the Earth’s Coriolis force on the large-scale circulation of turbulent Rayleigh–Bénard convection. Phys. Fluids 18 (12), 125108.Google Scholar
Brown, E. & Ahlers, G. 2006b Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.Google Scholar
Brown, E. & Ahlers, G. 2008 A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20 (7), 075101.Google Scholar
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech. 10005.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.Google Scholar
Kaczorowski, M., Shishkina, O., Shishkin, A., Wagner, C. & Xia, K.-Q. 2011 Analysis of the large-scale circulation and the boundary layers in turbulent Rayleigh–Bénard convection. In Direct and Large-Eddy Simulation VIII (ed. Kuerten, H., Geurts, B., Armenio, V. & Frhlich, J.), vol. 15, pp. 383–388. Springer.Google Scholar
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. E 65, 066306.CrossRefGoogle ScholarPubMed
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.Google Scholar
Qiu, X.-L. & Tong, P. 2001 Large-scale velocity structures in turbulent thermal convection. Phys. Rev. E 64, 036304.Google Scholar
Sano, M., Wu, X.-Z. & Libchaber, A. 1989 Turbulence in helium-gas free convection. Phys. Rev. A 40, 6421–6430.Google Scholar
Shang, X.-D. & Xia, K.-Q. 2001 Scaling of the velocity power spectra in turbulent thermal convection. Phys. Rev. E 64, 065301.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.CrossRefGoogle ScholarPubMed
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005a Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.Google Scholar
Sun, C. & Xia, K.-Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72, 067302.Google Scholar
Sun, C. & Xia, K.-Q. 2007 Multi-point local temperature measurements inside the conducting plates in turbulent thermal convection. J. Fluid Mech. 570, 479–489.CrossRefGoogle Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005b Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302.Google Scholar
Takeshita, T., Segawa, T., Glazier, J. A. & Sano, M. 1996 Thermal turbulence in mercury. Phys. Rev. Lett. 76, 1465–1468.Google Scholar
Weiss, S. & Ahlers, G. 2011 Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ratio $\Gamma = 0. 50$ and Prandtl number . J. Fluid Mech. 676, 5–40.Google Scholar
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75, 066307.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2008a Azimuthal motion, reorientation, cessation, and reversal of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 78, 036326.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2008b Flow mode transitions in turbulent thermal convection. Phys. Fluids 20 (5), 055104.Google Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.Google Scholar
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.Google Scholar
Xia, K.-Q. 2011 How heat transfer efficiencies in turbulent thermal convection depend on internal flow modes. J. Fluid Mech. 676, 1–4.Google Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.CrossRefGoogle ScholarPubMed
Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.Google Scholar
Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2007 Measured oscillations of the velocity and temperature fields in turbulent Rayleigh–Bénard convection in a rectangular cell. Phys. Rev. E 76, 036301.Google Scholar