Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T11:49:08.600Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and stability of gap-flow interference in a vibrating side-by-side arrangement of two circular cylinders

Published online by Cambridge University Press:  20 September 2018

B. Liu Open the ORCID record for B. Liu [Opens in a new window]  and
R. K. Jaiman Open the ORCID record for R. K. Jaiman [Opens in a new window]
B. Liu
Affiliation:
Department of Mechanical Engineering, National University of Singapore, Singapore 119077, Singapore
R. K. Jaiman
Affiliation:
Department of Mechanical Engineering, National University of Singapore, Singapore 119077, Singapore
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, the coupled dynamics of the gap flow and the vortex-induced vibration (VIV) of a side-by-side (SBS) arrangement of two circular cylinders is numerically investigated at Reynolds numbers 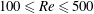$100\leqslant Re\leqslant 500$. The influence of VIV is incorporated by allowing one of the cylinders to vibrate freely in the transverse direction, which is termed as a vibrating side-by-side (VSBS) arrangement. A comparative three-dimensional study is performed between the stationary side-by-side (SSBS) and the VSBS arrangements to examine the characteristics of the complex coupling between the VIV and the gap flow. The results are also contrasted against the isolated configurations without any proximity and gap-flow interference. Of particular interest is to establish a relationship between the VIV, the gap flow and the near-wake instability behind bluff bodies. We find that the kinematics of the VIV regulates the streamwise vorticity concentration, which accompanies a recovery of the two-dimensional hydrodynamic response at the peak lock-in. Moreover, the near-wake instability may develop around an indeterminant two-dimensional streamline saddle point along the interfaces of a pair of imbalanced counter-signed vorticity clusters. The interaction between the imbalanced vorticity clusters and the gap-flow momentum are closely interlinked with the prominence of streamwise vortical structures. In both SSBS and VSBS arrangements, the flip-flopping frequency is significantly low for the three-dimensional flow, except at the VIV lock-in for the VSBS arrangement. While an early onset of VIV lock-in is observed for the vibrating configuration, a quasi-stable deflected gap-flow regime with stably deflected gap flow is found at the peak lock-in. The increase of the gap-flow proximity interference promotes the energy transfer and stabilizes the VIV lock-in. Finally, we employ the dynamic mode decomposition procedure to characterize the space–time evolution of the vortex wake system behind the cylinders.

JFM classification

Vortex Flows: Vortex Flows Wakes/Jets: Wakes/Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 804 - 838
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: Department of Mechanical Engineering, University of British Columbia, Vancouver, BC, V6T 1Z4, Canada. Email address for correspondence: [email protected]

References

Agrawal, A., Djenidi, L. & Antonia, R. A. 2006 Investigation of flow around a pair of side-by-side square cylinders using the lattice Boltzmann method. Comput. Fluids 35 (10), 1093–1107.Google Scholar
Alam, M. M. & Sakamoto, H. 2005 Investigation of Strouhal frequencies of two staggered bluff bodies and detection of multistable flow by wavelets. J. Fluids Struct. 20 (3), 425–449.Google Scholar
Bearman, P. W. & Wadcock, A. J. 1973 The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 61 (03), 499–511.Google Scholar
Blackburn, H. M., Govardhan, R. N. & Williamson, C. H. K. 2001 A complementary numerical and physical investigation of vortex-induced vibration. J. Fluids Struct. 15 (3), 481–488.Google Scholar
Carini, M., Giannetti, F. & Auteri, F. 2014 On the origin of the flip–flop instability of two side-by-side cylinder wakes. J. Fluid Mech. 742, 552–576.Google Scholar
Huang, N. E. 2014 Hilbert-Huang Transform and its Applications, vol. 16. World Scientific.Google Scholar
Huang, Z., Narasimhamurthy, V. D. & Andersson, H. I. 2010 Oblique and cellular vortex shedding behind a circular cylinder in a bidirectional shear flow. Phys. Fluids 22 (11), 114105.Google Scholar
Hunt, J. C. R., Wray, A. & Moin, P.1988 Eddies, stream, and convergence zones in turbulent flows. Tech. Rep. Center for Turbulence Research Report.Google Scholar
Ishigai, S., Nishikawa, E., Nishimura, K. & Cho, K. 1972 Experimental study on structure of gas flow in tube banks with tube axes normal to flow. Part 1. Kármán vortex flow from two tubes at various spacings. Bull. JSME 15 (86), 949–956.Google Scholar
Jaiman, R. K., Guan, M. Z. & Miyanawala, T. P. 2016a Partitioned iterative and dynamic subgrid-scale methods for freely vibrating square-section structure in turbulent flow. Comput. Fluids 133, 68–89.Google Scholar
Jaiman, R. K., Pillalamarri, N. R. & Guan, M. Z. 2016b A stable second-order partitioned iterative scheme for freely vibrating low-mass bluff bodies in a uniform flow. Comput. Methods Appl. Mech. Engng 301, 187–215.Google Scholar
Jaiman, R. K., Sen, S. & Gurugubelli, P. 2015 A fully implicit combined field scheme for freely vibrating square cylinders with sharp and rounded corners. Comput. Fluids 112, 1–18.Google Scholar
Jansen, K. E., Whiting, C. H. & Hulbert, G. M. 2000 A generalized-𝛼 method for integrating the filtered navier–stokes equations with a stabilized finite element method. Comput. Methods Appl. Mech. Engng 190 (3–4), 305–319.Google Scholar
Jovanovic, M. R., Schmid, P. J. & Nichols, J. W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26 (2), 024103.Google Scholar
Kang, S. 2003 Characteristics of flow over two circular cylinders in a side-by-side arrangement at low Reynolds numbers. Phys. Fluids 15 (9), 2486–2498.Google Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34 (1), 83–113.Google Scholar
Kim, H. J. 1988 Investigation of the flow between a pair of circular cylinders in the flopping regime. J. Fluid Mech. 196, 431–448.Google Scholar
Lankadasu, A. & Vengadesan, S. 2008 Onset of vortex shedding in planar shear flow past a square cylinder. Intl J. Heat Fluid Flow 29 (4), 1054–1059.Google Scholar
Le Dizes, S. & Laporte, F. 2002 Theoretical predictions for the elliptical instability in a two-vortex flow. J. Fluid Mech. 471, 169–201.Google Scholar
Leblanc, S. 1997 Stability of stagnation points in rotating flows. Phys. Fluids 9 (11), 3566–3569.Google Scholar
Lei, C., Cheng, L. & Kavanagh, K. 2001 Spanwise length effects on three-dimensional modelling of flow over a circular cylinder. Comput. Meth. Appl. Mech. Engng 190 (22), 2909–2923.Google Scholar
Leontini, J. S., Stewart, B. E., Thompson, M. C. & Hourigan, K. 2006 Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 18 (6), 067101.Google Scholar
Li, Z., Yao, W., Yang, K., Jaiman, R. K. & Khoo, B. C. 2016 On the vortex-induced oscillations of a freely vibrating cylinder in the vicinity of a stationary plane wall. J. Fluids Struct. 65, 495–526.Google Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids A 3 (11), 2644–2651.Google Scholar
Lin, J. C., Yang, Y. & Rockwell, D. 2002 Flow past two cylinders in tandem: instantaneous and averaged flow structure. J. Fluids Struct. 16 (8), 1059–1071.Google Scholar
Liu, B. & Jaiman, R. K. 2016 Interaction dynamics of gap flow with vortex-induced vibration in side-by-side cylinder arrangement. Phys. Fluids 28 (12), 127103.Google Scholar
Meunier, P., Le Dizes, S. & Leweke, T. 2005 Physics of vortex merging. C. R. Phys. 6 (4), 431–450.Google Scholar
Mizushima, J. & Ino, Y. 2008 Stability of flows past a pair of circular cylinders in a side-by-side arrangement. J. Fluid Mech. 595, 491–507.Google Scholar
Mysa, R. C., Kaboudian, A. & Jaiman, R. K. 2016 On the origin of wake-induced vibration in two tandem circular cylinders at low Reynolds number. J. Fluids Struct. 61, 76–98.Google Scholar
Papaioannou, G. V., Yue, D. K. P., Triantafyllou, M. S. & Karniadakis, G. E. 2006 Three-dimensionality effects in flow around two tandem cylinders. J. Fluid Mech. 558, 387–413.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19 (1), 125–155.Google Scholar
Persillon, H. & Braza, M. 1998 Physical analysis of the transition to turbulence in the wake of a circular cylinder by three-dimensional Navier–Stokes simulation. J. Fluid Mech. 365, 23–88.Google Scholar
Peschard, I. & Le Gal, P. 1996 Coupled wakes of cylinders. Phys. Rev. Lett. 77 (15), 3122–3125.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schmid, P. J., Li, L., Juniper, M. P. & Pust, O. 2011 Applications of the dynamic mode decomposition. Theor. Comput. Fluid Dyn. 25 (1–4), 249–259.Google Scholar
Sumner, D. 2010 Two circular cylinders in cross-flow: A review. J. Fluids Struct. 26 (6), 849–899.Google Scholar
Sumner, D., Price, S. J. & Paidoussis, M. P. 2000 Flow-pattern identification for two staggered circular cylinders in cross-flow. J. Fluid Mech. 411, 263–303.Google Scholar
Sumner, D., Wong, S. S. T., Price, S. J. & Paidoussis, M. P. 1999 Fluid behaviour of side-by-side circular cylinders in steady cross-flow. J. Fluids Struct. 13 (3), 309–338.Google Scholar
Szepessy, S. & Bearman, P. W. 1992 Aspect ratio and end plate effects on vortex shedding from a circular cylinder. J. Fluid Mech. 234, 191–217.Google Scholar
Wieselsberger, C. 1921 Neuere Feststellungen uber die gesetze des Flussigkeits und Luftwiderstands. Phys. Z. 22, 321.Google Scholar
Williamson, C. H. K. 1985 Evolution of a single wake behind a pair of bluff bodies. J. Fluid Mech. 159, 1–18.Google Scholar
Williamson, C. H. K. 1996a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Williamson, C. H. K. 1996b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.Google Scholar
Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1 (2), 239–261.Google Scholar
Zhang, H.-Q., Fey, U., Noack, B. R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.Google Scholar
Zhao, M., Cheng, L., An, H. & Lu, L. 2014 Three-dimensional numerical simulation of vortex-induced vibration of an elastically mounted rigid circular cylinder in steady current. J. Fluids Struct. 50, 292–311.Google Scholar
Zhou, Y. & Antonia, R. A. 1994 Critical points in a turbulent near wake. J. Fluid Mech. 275, 59–81.Google Scholar