Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T12:06:57.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag of a heated sphere at low Reynolds numbers in the absence of buoyancy

Published online by Cambridge University Press:  23 April 2019

Swetava Ganguli Open the ORCID record for Swetava Ganguli [Opens in a new window]  and
Sanjiva K. Lele
Swetava Ganguli*
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA Department of Computer Science, Stanford University, Stanford, CA 94305, USA
Sanjiva K. Lele
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA Department of Aeronautics and Astronautics, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

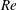Fully resolved simulations are used to quantify the effects of heat transfer in the absence of buoyancy on the drag of a spatially fixed heated spherical particle at low Reynolds numbers ($Re$) in the range 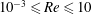$10^{-3}\leqslant Re\leqslant 10$ in a variable-property fluid. The case where buoyancy is present is analysed in a subsequent paper. This analysis is carried out without making any assumptions on the amount of heat addition from the sphere and thus encompasses both the heating regime where the Boussinesq approximation holds and the regime where it breaks down. The particle is assumed to have a low Biot number, which means that the particle is uniformly at the same temperature and has no internal temperature gradients. Large deviations in the value of the drag coefficient as the temperature of the sphere increases are observed. When 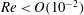$Re<O(10^{-2})$, these deviations are explained using a low-Mach-number perturbation analysis as irrotational corrections to a Stokes–Oseen base flow. Correlations for the drag and Nusselt number of a heated sphere are proposed for the range of Reynolds numbers 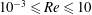$10^{-3}\leqslant Re\leqslant 10$ which fit the computationally obtained values with less than 1 % and 3 % errors, respectively. These correlations can be used in simulations of gas–solid flows where the accuracy of the drag law affects the prediction of the overall flow behaviour. Finally, an analogy to incompressible flow over a modified sphere is demonstrated.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 264 - 291
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Goddard, J. D. 1965 Asympotic expansions for laminar forced-convection heat and mass transfer. Part 1. Low speed flows. J. Fluid Mech. 23, 273–291.Google Scholar
Acrivos, A. & Taylor, T. D. 1962 Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 5, 387–394.Google Scholar
Ansari, A. & Morris, S. 1985 The effects of a strongly temperature-dependent viscosity on Stokes drag law: experiments and theory. J. Fluid Mech. 159, 459.Google Scholar
Boussinesq, J. 1903 Theorie Analytique de la Chaleur. L’Ecole Polytechnique, Paris.Google Scholar
Breach, D. R. 1961 Slow flow past ellipsoids of revolution. J. Fluid Mech. 10, 306–314.Google Scholar
Brenner, H. 1961 The Oseen resistance of a particle of arbitrary shape. J. Fluid Mech. 11, 604–610.Google Scholar
Brenner, H. 1963 Forced convection heat and mass transfer at small Peclet numbers from a particle of arbitrary shape. Chem. Engng Sci. 18, 109–122.Google Scholar
Brenner, H. 1964 The Stokes resistance of a slightly deformed sphere. Chem. Engng Sci. 19, 519–539.Google Scholar
Brenner, H. & Cox, R. G. 1963 The resistance to a particle of arbitrary shape in translational motion at small Reynolds numbers. J. Fluid Mech. 17, 561–595.Google Scholar
Chester, W. 1962 On Oseen’s approximation. J. Fluid Mech. 13, 557–569.Google Scholar
Chester, W., Breach, D. R. & Proudman, I. 1969 On the flow past a sphere at low Reynolds number. J. Fluid Mech. 37 (04), 751–760.Google Scholar
Clift, R. & Gauvin, W. H. 1970 Proc. Chemeca ’70 1, 14–28.Google Scholar
Clift, R., Grace, J. & Weber, M. E. 1978 Bubbles, Drops and Particles. Dover.Google Scholar
Collins, W. D. 1963 A note on the axisymmetric Stokes flow of viscous fluid past a spherical gap. Mathematika 10, 72–78.Google Scholar
Dennis, S. C. R., Walker, J. D. A. & Hudson, J. D. 1973 Heat transfer from a sphere at low Reynolds numbers. J. Fluid Mech. 60, 273–283.Google Scholar
Ganguli, S.2018 Computational analysis of canonical problems arising in the interaction of heated particles and a fluid. PhD thesis, Stanford University.Google Scholar
Goldstein, S. 1929 The forces on a solid body moving through a viscous fluid. Proc. R. Soc. Ser. A 131 (816), 198–208.Google Scholar
Hadamard, J. S. 1911 Mouvement permanent lent d’une sphere liquide et visqueuse dans un liquide visqueux. C. R. Acad. Sci. 152, 1735–1738.Google Scholar
Ham, F. 2007 An efficient scheme for large eddy simulation of low-Ma combustion in complex configurations. In Center for Turbulence Research, Annual Res. Briefs, Stanford University.Google Scholar
Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
Kaplun, S. 1957 Low Reynolds number flow past a circular cylinder. J. Math. Mech. 6, 595.Google Scholar
Kaplun, S. & Lagerstrom, P. A. 1957 Asymptotic expansions of Navier–Stokes solutions for small Reynolds numbers. J. Math. Mech. 6, 585–593.Google Scholar
Kassoy, D. R., Adamson, T. C. & Messiter, A. F. 1966 Compressible low Reynolds number flow around a sphere. Phys. Fluids 9 (4), 671–681.Google Scholar
Kundu, P. K., Cohen, I. M. & Dowling, D. R. 2014 Fluid Mechanics. Academic Press.Google Scholar
Kurose, R., Anami, M., Fujita, A. & Komori, S. 2012 Numerical simulation of flow past a heated/cooled sphere. J. Fluid Mech. 692, 332–346.Google Scholar
Lagerstrom, P. A. 1964 Laminar Flow Theory. Princeton University Press.Google Scholar
Lagerstrom, P. A. 1988 Matched Asymptotic Expansions – Ideas and Techniques, Applied Mathematical Series, vol. 76. Springer.Google Scholar
Lagerstrom, P. A. & Cole, J. D. 1955 Examples illustrating expansion procedures for the Navier–Stokes equations. J. Rat. Mech. Anal. 4, 817–882.Google Scholar
Lamb, H. 1911 On the uniform motion of a sphere through a viscous fluid. Phil. Mag. 21, 112–121.Google Scholar
Lapple, C. E.1951 Particle Dynamics. Tech. Rep.. Eng. Res. Lab., E. I. Dupont de Nemours and Co., Wilmington, Delaware.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.Google Scholar
Levich, V. G. 1962 Physicochemical Hydrodynamics. Prentice-Hall.Google Scholar
Lewis, J. A. & Carrier, F. G. 1949 Some remarks on the flat plate boundary layer. Q. Appl. Maths 7, 228–234.Google Scholar
Masliyah, J. H. & Epstein, N. 1972 Numerical solution of heat and mass transfer from spheroids in axisymmetric flow. Prog. Heat Mass Transfer 6, 613–632.Google Scholar
Nguyen, T. H.1973 Heats of mixing: measurement and prediction by an analytical group solution model. PhD Thesis, McGill University.Google Scholar
Oberbeck, A. 1876 Über stationäre Flüssigkeit bewegungen mit Berücksichtigung der inneren Reibung. Crelle’s J. 81, 62–80.Google Scholar
O’Brien, V.1965a Deformed spheroids in Stokes flow. Appl. Phys. Lab. Rep. TG-716, Johns Hopkins University, Silver Spring.Google Scholar
O’Brien, V. 1965b Eggs and other deformed spheroids in Stokes flow. APL Technical Digest 4, 11–16.Google Scholar
O’Brien, V. 1966 Stokes flow about deformed spheroids. Intl. J. Engng. Sci. 4, 925–937.Google Scholar
O’Brien, V. 1968 Form factors for deformed spheroids in Stokes flow. AIChE J. 14, 870–875.Google Scholar
Oppenheimer, N., Navardi, S. & Stone, H. A. 2016 Motion of a hot particle in viscous fluids. Phys. Rev. Fluids 1, 014001.Google Scholar
Oseen, C. W. 1910 Über die Stoke’sche Formel, und über eine verwandte Aufgabe in der Hydrodynamik. Ark. Mat. Astron. Fys. 6 (29).Google Scholar
Panton, R. L. 2005 Incompressible Flow, 3rd edn. John Wiley.Google Scholar
Payne, L. E. & Pell, W. H. 1960 The Stokes flow problem for a class of axially symmetric bodies. J. Fluid Mech. 7, 529–549.Google Scholar
Proudman, I. & Pearson, J. R. A. 1957 Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 2, 237–262.Google Scholar
Rings, D., Schachoff, R., Selmke, M., Cichos, F. & Kroy, K. 2010 Hot Brownian motion. Phys. Rev. Lett. 105, 090604.Google Scholar
Rybczynski, W. 1911 Über die fortschreitende Bewegung einer flüssigen Kugel in einem zähen Medium. Bull. Acad. Sci. Cracovie A, 40–46.Google Scholar
Sazhin, S. S. 2006 Advanced models of fuel droplet heating and evaporation. Prog. Energy Combust. Sci. 32, 162–214.Google Scholar
Schiller, L. & Nauman, A. Z. 1933 Uber die grundlegenden Berechnungen bei der Schwekraftaubereitung. Z. Verein. Deutsch. Ing. 77 (12), 318–320.Google Scholar
Shakespear, G. A. 1914 Experiments on the resistance of the air to falling spheres. Phil. Mag. 28, 728–734.Google Scholar
Spiegel, E. A. & Veronis, G. 1960 On the Boussinesq approximation for a compressible fluid. J. Astrophys. 131, 442–447.Google Scholar
Stinberger, E. H., Pruppacher, H. R. & Neiburger, M. 1968 On the hydrodynamics of pairs of spheres falling along their line of centres in a viscous medium. J. Fluid Mech. 34, 809–819.Google Scholar
Stokes, G. G. 1851 On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 9 (Part II), 8–106.Google Scholar
Taylor, T. D. & Acrivos, A. 1964 On the deformation and drag of a falling viscous drop at low Reynolds number. J. Fluid Mech. 18, 466–476.Google Scholar
Van Dyke, M. D. 1964 Perturbation Methods in Fluid Dynamics. Academic Press.Google Scholar
Van Dyke, M. D. 1970 Extension of Goldstein’s series for the Oseen drag of a sphere. J. Fluid Mech. 44, 365–372.Google Scholar
Vapnik, V. N. 1998 Statistical Learning Theory. John Wiley.Google Scholar
Vincenti, W. G. & Kruger, C. H. 1965 Introduction to Physical Gas Dynamics. John Wiley.Google Scholar
Whitehead, A. N. 1889 Second approximations to viscous fluid motion. Q. J. Maths 23, 143–152.Google Scholar
Yih, C. S. 1969 Fluid Mechanics. McGraw-Hill.Google Scholar