Published online by Cambridge University Press: 16 November 2018
When a deep body of fluid with a stable salinity gradient is heated from below at a horizontal boundary a destabilizing temperature gradient develops and can lead to instabilities. We will focus on two variants of this problem: the sudden increase in the boundary temperature at the initial time and the sudden turning on of a constant heat flux. These generate time-dependent temperature profiles. We look at the growing phase of the linear instabilities as an initial value problem where the initial time for the instabilities is a parameter to be determined. We determine numerically the optimal initial conditions and the optimal starting time for the instabilities to ensure that the maximum growth occurs at some given later time. The method that is used is an extension of the method developed by Kerr & Gumm (J. Fluid Mech., vol. 825, 2017, pp. 1002–1034) in their investigation of the stability of developing temperature boundary layers at horizontal and vertical boundaries. This requires the use of an appropriate measure of the amplitude of the disturbances which is identified. The effectiveness of this approach is verified by looking at the classic problem of double-diffusive convection in a horizontal layer, where we look at both the salt-finger regime and the diffusive regime. We show that this approach is an effective way of investigating instabilities where the background gradients time dependent. For the problem of heating a salinity gradient from below, as the heat diffuses into the fluid the effective thermal Rayleigh number based on the instantaneous diffusion length scale grows. For the case of a sudden increase in the temperature by a fixed amount the effective thermal Rayleigh number is proportional to 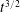 $t^{3/2}$, and for a constant heat flux it is proportional to
$t^{3/2}$, and for a constant heat flux it is proportional to 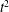 $t^{2}$, where
$t^{2}$, where  $t$ is the time since the onset of heating. However, the effective salt Rayleigh number also grows as
$t$ is the time since the onset of heating. However, the effective salt Rayleigh number also grows as 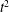 $t^{2}$. We will show that for the constant temperature case the thermal Rayleigh number initially dominates and the instabilities undergo a phase where the convection is essentially thermal, and the onset is essentially instantaneous. As the salt Rayleigh number becomes more significant the instability undergoes a transition to oscillatory double-diffusive convection. For the constant heat flux the ratio of the thermal and salt Rayleigh numbers is constant, and the instabilities are always double diffusive in their nature. These instabilities initially decay. Hence, to achieve the largest growth at some given fixed time, there is an optimal time after the onset of heating for the instabilities to be initiated. These instabilities are essentially double diffusive throughout their growth.
$t^{2}$. We will show that for the constant temperature case the thermal Rayleigh number initially dominates and the instabilities undergo a phase where the convection is essentially thermal, and the onset is essentially instantaneous. As the salt Rayleigh number becomes more significant the instability undergoes a transition to oscillatory double-diffusive convection. For the constant heat flux the ratio of the thermal and salt Rayleigh numbers is constant, and the instabilities are always double diffusive in their nature. These instabilities initially decay. Hence, to achieve the largest growth at some given fixed time, there is an optimal time after the onset of heating for the instabilities to be initiated. These instabilities are essentially double diffusive throughout their growth.