 $\text{SSP}/\text{VWI}$ states by a stable stratification
$\text{SSP}/\text{VWI}$ states by a stable stratificationPublished online by Cambridge University Press: 06 November 2015
We identify ‘minimal seeds’ for turbulence, i.e. initial conditions of the smallest possible total perturbation energy density 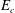 $E_{c}$ that trigger turbulence from the laminar state, in stratified plane Couette flow, the flow between two horizontal plates of separation
$E_{c}$ that trigger turbulence from the laminar state, in stratified plane Couette flow, the flow between two horizontal plates of separation 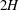 $2H$, moving with relative velocity
$2H$, moving with relative velocity 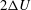 $2{\rm\Delta}U$, across which a constant density difference
$2{\rm\Delta}U$, across which a constant density difference 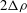 $2{\rm\Delta}{\it\rho}$ from a reference density
$2{\rm\Delta}{\it\rho}$ from a reference density 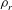 ${\it\rho}_{r}$ is maintained. To find minimal seeds, we use the ‘direct-adjoint-looping’ (DAL) method for finding nonlinear optimal perturbations that optimise the time-averaged total dissipation of energy in the flow. These minimal seeds are located adjacent to the edge manifold, the manifold in state space that separates trajectories which transition to turbulence from those which eventually decay to the laminar state. The edge manifold is also the stable manifold of the system’s ‘edge state’. Therefore, the trajectories from the minimal seed initial conditions spend a large amount of time in the vicinity of some states: the edge state; another state contained within the edge manifold; or even in dynamically slowly varying regions of the edge manifold, allowing us to investigate the effects of a stable stratification on any coherent structures associated with such states. In unstratified plane Couette flow, these coherent structures are manifestations of the self-sustaining process (SSP) deduced on physical grounds by Waleffe (Phys. Fluids, vol. 9, 1997, pp. 883–900), or equivalently finite Reynolds number solutions of the vortex–wave interaction (VWI) asymptotic equations initially derived mathematically by Hall & Smith (J. Fluid Mech., vol. 227, 1991, pp. 641–666). The stratified coherent states we identify at moderate Reynolds number display an altered form from their unstratified counterparts for bulk Richardson numbers
${\it\rho}_{r}$ is maintained. To find minimal seeds, we use the ‘direct-adjoint-looping’ (DAL) method for finding nonlinear optimal perturbations that optimise the time-averaged total dissipation of energy in the flow. These minimal seeds are located adjacent to the edge manifold, the manifold in state space that separates trajectories which transition to turbulence from those which eventually decay to the laminar state. The edge manifold is also the stable manifold of the system’s ‘edge state’. Therefore, the trajectories from the minimal seed initial conditions spend a large amount of time in the vicinity of some states: the edge state; another state contained within the edge manifold; or even in dynamically slowly varying regions of the edge manifold, allowing us to investigate the effects of a stable stratification on any coherent structures associated with such states. In unstratified plane Couette flow, these coherent structures are manifestations of the self-sustaining process (SSP) deduced on physical grounds by Waleffe (Phys. Fluids, vol. 9, 1997, pp. 883–900), or equivalently finite Reynolds number solutions of the vortex–wave interaction (VWI) asymptotic equations initially derived mathematically by Hall & Smith (J. Fluid Mech., vol. 227, 1991, pp. 641–666). The stratified coherent states we identify at moderate Reynolds number display an altered form from their unstratified counterparts for bulk Richardson numbers 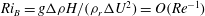 $\mathit{Ri}_{B}=g{\rm\Delta}{\it\rho}H/({\it\rho}_{r}{\rm\Delta}U^{2})=O(\mathit{Re}^{-1})$, and exhibit chaotic motion for larger
$\mathit{Ri}_{B}=g{\rm\Delta}{\it\rho}H/({\it\rho}_{r}{\rm\Delta}U^{2})=O(\mathit{Re}^{-1})$, and exhibit chaotic motion for larger 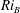 $\mathit{Ri}_{B}$. We demonstrate that at hith Reynolds number the suppression of vertical motions by stratification strongly disrupts input from the waves to the roll velocity structures, thus preventing the waves from reinforcing the viscously decaying roll structures adequately, when
$\mathit{Ri}_{B}$. We demonstrate that at hith Reynolds number the suppression of vertical motions by stratification strongly disrupts input from the waves to the roll velocity structures, thus preventing the waves from reinforcing the viscously decaying roll structures adequately, when 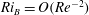 $\mathit{Ri}_{B}=O(\mathit{Re}^{-2})$.
$\mathit{Ri}_{B}=O(\mathit{Re}^{-2})$.
Evolution in time of the isosurfaces of streamwise velocity u = 0.6 max(u) (blue) and u = -0.6 max(u) (red) for the minimal seed trajectories in the narrow geometry N. RiB= 0 (top left), 10-4 (top middle), 10-3(top right), 3x10-3 (bottom left) and 10-2 (bottom middle). Counter in the bottom right corner shows time in advective units.
Evolution in time of the isosurfaces of streamwise velocity u = 0.6 max(u) (blue) and u = -0.6 max(u) (red) for the minimal seed trajectories in the narrow geometry N. RiB= 0 (top left), 10-4 (top middle), 10-3(top right), 3x10-3 (bottom left) and 10-2 (bottom middle). Counter in the bottom right corner shows time in advective units.
Evolution in time of the isosurfaces of streamwise velocity u = 0.6 max(u) (blue) and u = -0.6 max(u) (red) for the minimal seed trajectories in the wide geometry W. RiB = 0 (top left), 3x10-3 (top right) and 10-2(bottom left). Counter in the bottom right corner shows time in advective units.
Evolution in time of the isosurfaces of streamwise velocity u = 0.6 max(u) (blue) and u = -0.6 max(u) (red) for the minimal seed trajectories in the wide geometry W. RiB = 0 (top left), 3x10-3 (top right) and 10-2(bottom left). Counter in the bottom right corner shows time in advective units.