Published online by Cambridge University Press: 11 July 2008
Fully developed incompressible turbulent pipe flow at bulk-velocity- and pipe-diameter-based Reynolds number ReD=44000 was simulated with second-order finite-difference methods on 630 million grid points. The corresponding Kármán number R+, based on pipe radius R, is 1142, and the computational domain length is 15R. The computed mean flow statistics agree well with Princeton Superpipe data at ReD=41727 and at ReD=74000. Second-order turbulence statistics show good agreement with experimental data at ReD=38000. Near the wall the gradient of 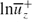 with respect to ln(1−r)+ varies with radius except for a narrow region, 70 < (1−r)+ < 120, within which the gradient is approximately 0.149. The gradient of
with respect to ln(1−r)+ varies with radius except for a narrow region, 70 < (1−r)+ < 120, within which the gradient is approximately 0.149. The gradient of 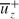 with respect to ln{(1−r)++a+} at the present relatively low Reynolds number of ReD=44000 is not consistent with the proposition that the mean axial velocity
with respect to ln{(1−r)++a+} at the present relatively low Reynolds number of ReD=44000 is not consistent with the proposition that the mean axial velocity 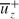 is logarithmic with respect to the sum of the wall distance (1−r)+ and an additive constant a+ within a mesolayer below 300 wall units. For the standard case of a+=0 within the narrow region from (1−r)+=50 to 90, the gradient of
is logarithmic with respect to the sum of the wall distance (1−r)+ and an additive constant a+ within a mesolayer below 300 wall units. For the standard case of a+=0 within the narrow region from (1−r)+=50 to 90, the gradient of 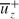 with respect to ln{(1−r)++a+} is approximately 2.35. Computational results at the lower Reynolds number ReD=5300 also agree well with existing data. The gradient of
with respect to ln{(1−r)++a+} is approximately 2.35. Computational results at the lower Reynolds number ReD=5300 also agree well with existing data. The gradient of 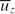 with respect to 1−r at ReD=44000 is approximately equal to that at ReD=5300 for the region of 1−r > 0.4. For 5300 < ReD < 44000, bulk-velocity-normalized mean velocity defect profiles from the present DNS and from previous experiments collapse within the same radial range of 1−r > 0.4. A rationale based on the curvature of mean velocity gradient profile is proposed to understand the perplexing existence of logarithmic mean velocity profile in very-low-Reynolds-number pipe flows. Beyond ReD=44000, axial turbulence intensity varies linearly with radius within the range of 0.15 < 1−r < 0.7. Flow visualizations and two-point correlations reveal large-scale structures with comparable near-wall azimuthal dimensions at ReD=44000 and 5300 when measured in wall units. When normalized in outer units, streamwise coherence and azimuthal dimension of the large-scale structures in the pipe core away from the wall are also comparable at these two Reynolds numbers.
with respect to 1−r at ReD=44000 is approximately equal to that at ReD=5300 for the region of 1−r > 0.4. For 5300 < ReD < 44000, bulk-velocity-normalized mean velocity defect profiles from the present DNS and from previous experiments collapse within the same radial range of 1−r > 0.4. A rationale based on the curvature of mean velocity gradient profile is proposed to understand the perplexing existence of logarithmic mean velocity profile in very-low-Reynolds-number pipe flows. Beyond ReD=44000, axial turbulence intensity varies linearly with radius within the range of 0.15 < 1−r < 0.7. Flow visualizations and two-point correlations reveal large-scale structures with comparable near-wall azimuthal dimensions at ReD=44000 and 5300 when measured in wall units. When normalized in outer units, streamwise coherence and azimuthal dimension of the large-scale structures in the pipe core away from the wall are also comparable at these two Reynolds numbers.