Article contents
Direct numerical simulation of a non-equilibrium three-dimensional turbulent boundary layer over a flat plate
Published online by Cambridge University Press: 09 September 2020
Abstract
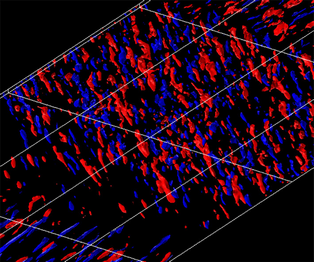
Direct numerical simulations (DNS) are used to examine a spatially developing non-equilibrium three-dimensional turbulent boundary layer (3DTBL) over a flat plate. The present flow is a ‘shear-driven’ 3DTBL owing to a sudden imposition of a surface spanwise velocity  ${W_S}$. Particular attention is given to the effects of cross-flow and Reynolds number. In the DNS, three values of the inlet momentum thickness Reynolds number,
${W_S}$. Particular attention is given to the effects of cross-flow and Reynolds number. In the DNS, three values of the inlet momentum thickness Reynolds number,  $R{e_{{\theta _0}}} = 300$, 600 and 900, are used with several values of
$R{e_{{\theta _0}}} = 300$, 600 and 900, are used with several values of  ${W_S}$. The present largest
${W_S}$. The present largest  ${W_S}$ is twice the free-stream velocity
${W_S}$ is twice the free-stream velocity  ${U_0}$, comparable to the maximum value of the spinning cylinder experiment by Lohmann (Trans. ASME I: J. Fluids Engng, vol. 98, 1976, pp. 354–363). After imposing
${U_0}$, comparable to the maximum value of the spinning cylinder experiment by Lohmann (Trans. ASME I: J. Fluids Engng, vol. 98, 1976, pp. 354–363). After imposing  ${W_S}$, the mean streamwise vorticity
${W_S}$, the mean streamwise vorticity  ${\overline \varOmega _x}$ increasingly propagates away from the wall where there is close relationship between a deficit of mean streamwise velocity and inviscid skewing (i.e. three-dimensionality). At a downstream station of a 3DTBL, near-plateaus appear in the skin friction coefficients where the magnitudes depend intrinsically on
${\overline \varOmega _x}$ increasingly propagates away from the wall where there is close relationship between a deficit of mean streamwise velocity and inviscid skewing (i.e. three-dimensionality). At a downstream station of a 3DTBL, near-plateaus appear in the skin friction coefficients where the magnitudes depend intrinsically on  ${W_S}$. The approach to the collateral state is, however, slow for mean streamwise velocity
${W_S}$. The approach to the collateral state is, however, slow for mean streamwise velocity  $\overline U$ where the Reynolds shear stress
$\overline U$ where the Reynolds shear stress  $\overline {uv}$ extracts energy from the mean flow inefficiently. As the Reynolds number increases, the mean velocity magnitude
$\overline {uv}$ extracts energy from the mean flow inefficiently. As the Reynolds number increases, the mean velocity magnitude  ${Q_r}$ tends to show the log law but with a larger von Kármán constant than in a two-dimensional turbulent boundary layer. Instantaneously, toppling u structures dominate owing to cross-flow and become more prominent with increasing Re. Statistically, the latter spanwise length scale increases linearly with respect to y below y/δ99 = 0.2, which indicates that cross-flow yields a self-similar behaviour.
${Q_r}$ tends to show the log law but with a larger von Kármán constant than in a two-dimensional turbulent boundary layer. Instantaneously, toppling u structures dominate owing to cross-flow and become more prominent with increasing Re. Statistically, the latter spanwise length scale increases linearly with respect to y below y/δ99 = 0.2, which indicates that cross-flow yields a self-similar behaviour.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 10
- Cited by



