Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Ming
Li, Mingshui
and
Yang, Yang
2018.
A statistical approach to the identification of the two-dimensional aerodynamic admittance of streamlined bridge decks.
Journal of Fluids and Structures,
Vol. 83,
Issue. ,
p.
372.
Li, Ming
Li, Mingshui
and
Su, Yi
2019.
Experimental determination of the two-dimensional aerodynamic admittance of typical bridge decks.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 193,
Issue. ,
p.
103975.
Li, Ming
Li, Mingshui
Zhong, Yingzi
and
Luo, Nan
2019.
Buffeting response evaluation of long-span bridges with emphasis on the three-dimensional effects of gusty winds.
Journal of Sound and Vibration,
Vol. 439,
Issue. ,
p.
156.
Yang, Yang
Li, Mingshui
and
Liao, Haili
2019.
Three-dimensional effects on the transfer function of a rectangular-section body in turbulent flow.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
348.
Yang, Yang
Li, Mingshui
Su, Yi
and
Sun, Yanguo
2019.
Aerodynamic admittance of a 5:1 rectangular cylinder in turbulent flow.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 189,
Issue. ,
p.
125.
Su, Yi
and
Li, Mingshui
2019.
Integrated transfer function for buffeting response evaluation of long-span bridges.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 189,
Issue. ,
p.
231.
Li, Mingshui
Li, Ming
and
Yang, Yang
2020.
Strategy for the determination of unsteady aerodynamic forces on elongated bodies in grid-generated turbulent flow.
Experimental Thermal and Fluid Science,
Vol. 110,
Issue. ,
p.
109939.
Du, Shubi
Li, Mingshui
and
Yang, Yang
2020.
Effects of turbulence integral scales on characteristics of fluctuating wind pressures.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 204,
Issue. ,
p.
104245.
Yang, Yang
Li, Mingshui
Kim, Ho-Kyung
and
Li, Ming
2020.
Measurements of fluctuating lift forces on rectangular cylinders in turbulent flow.
Physics of Fluids,
Vol. 32,
Issue. 1,
Zhao, Lin
Xie, Xi
Wu, Teng
Li, Shao-peng
Li, Zhi-peng
Ge, Yao-jun
and
Kareem, Ahsan
2020.
Revisiting aerodynamic admittance functions of bridge decks.
Journal of Zhejiang University-SCIENCE A,
Vol. 21,
Issue. 7,
p.
535.
Smith, Samuel M.
Brandner, Paul A.
Pearce, Bryce W.
Venning, James A.
Moreau, Danielle J.
and
Clarke, David B.
2021.
Steady and unsteady loading on a hydrofoil immersed in a turbulent boundary layer.
Journal of Fluids and Structures,
Vol. 102,
Issue. ,
p.
103225.
Su, Yi
Di, Jin
Li, Jinzhe
and
Xia, Fan
2022.
Wind Pressure Field Reconstruction and Prediction of Large-Span Roof Structure with Folded-Plate Type Based on Proper Orthogonal Decomposition.
Applied Sciences,
Vol. 12,
Issue. 17,
p.
8430.
Li, Mingshui
Zhao, Yongfei
Yang, Yang
and
Zhou, Qiang
2022.
Aerodynamic lift fluctuations of an airfoil in various turbulent flows.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Su, Yi
Di, Jin
Zuo, Tingzhong
Li, Shaopeng
and
Qin, Fengjiang
2022.
Buffeting response evaluation of slender linear structures considering the influence of the aspect ratio on the scale effect.
Journal of Sound and Vibration,
Vol. 530,
Issue. ,
p.
116969.
Su, Yi
Di, Jin
Li, Shaopeng
Jian, Bin
and
Liu, Jun
2022.
Buffeting Response Prediction of Long-Span Bridges Based on Different Wind Tunnel Test Techniques.
Applied Sciences,
Vol. 12,
Issue. 6,
p.
3171.
Li, Ming
Li, Qiusheng
Shi, Haoyun
and
Li, Mingshui
2022.
Effects of free-stream turbulence on the near wake flow and aerodynamic forces of a square cylinder.
Journal of Fluids and Structures,
Vol. 114,
Issue. ,
p.
103748.
Jiadong, Zeng
Mingshui, Li
Zhiguo, Li
and
Zhitian, Zhang
2022.
Spatial correlation of along-wind fluctuating aerodynamic force acting on large aspect-ratio rectangular prisms.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 224,
Issue. ,
p.
104951.
Li, Ming
Li, Qiusheng
Shi, Hao-Yun
and
Li, Ming-Shui
2022.
Large-Scale Gust Effect on Aerodynamic Pressures and Forces on a Square Cylinder.
SSRN Electronic Journal ,
Wang, Yunfei
Chen, Xinzhong
and
Li, Yongle
2022.
Influence of Wind Turbulence on Aerodynamic Admittances of a Streamlined Bridge Deck at Different Angles of Attack.
Journal of Bridge Engineering,
Vol. 27,
Issue. 9,
Yao, Haoyu
Cao, Linlin
Wu, Dazhuan
Huang, Bin
Qin, Shijie
and
Yu, Faxin
2022.
Unsteady responses and correlation characteristics of propeller blades under turbulence excitation.
Ocean Engineering,
Vol. 266,
Issue. ,
p.
112631.
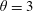 $\unicode[STIX]{x1D703}=3$, 5 and 7) are used. These wing models have an NACA 0015 profile cross-section and a fixed chord length
$\unicode[STIX]{x1D703}=3$, 5 and 7) are used. These wing models have an NACA 0015 profile cross-section and a fixed chord length 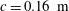 $c=0.16~\text{m}$. The testing results show that, at a fixed ratio of turbulence integral scale to chord, the deviation between the experimental one-wavenumber transfer function obtained from the strip assumption and the Sears function is reduced with increasing aspect ratio, as expected by the theoretical predictions. However, due to the effect of thickness, the experimental values at high frequencies cannot be captured by the Sears function which is derived based on the flat plate assumption. In practical applications, the effect of thickness on the transfer function should be considered.
$c=0.16~\text{m}$. The testing results show that, at a fixed ratio of turbulence integral scale to chord, the deviation between the experimental one-wavenumber transfer function obtained from the strip assumption and the Sears function is reduced with increasing aspect ratio, as expected by the theoretical predictions. However, due to the effect of thickness, the experimental values at high frequencies cannot be captured by the Sears function which is derived based on the flat plate assumption. In practical applications, the effect of thickness on the transfer function should be considered.