Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T07:22:31.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusion of inertia-gravity waves by geostrophic turbulence

Published online by Cambridge University Press:  30 April 2019

Hossein A. Kafiabad Open the ORCID record for Hossein A. Kafiabad [Opens in a new window] ,
Miles A. C. Savva  and
Jacques Vanneste Open the ORCID record for Jacques Vanneste [Opens in a new window]
Hossein A. Kafiabad
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, Edinburgh EH9 3FD, UK
Miles A. C. Savva
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, Edinburgh EH9 3FD, UK
Jacques Vanneste*
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, Edinburgh EH9 3FD, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The scattering of inertia-gravity waves by large-scale geostrophic turbulence in a rapidly rotating, strongly stratified fluid leads to the diffusion of wave energy on the constant-frequency cone in wavenumber space. We derive the corresponding diffusion equation and relate its diffusivity to the wave characteristics and the energy spectrum of the turbulent flow. We check the predictions of this equation against numerical simulations of the three-dimensional Boussinesq equations in initial-value and forced scenarios with horizontally isotropic wave and flow fields. 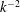In the forced case, wavenumber diffusion results in a $k^{-2}$ wave energy spectrum consistent with as-yet-unexplained features of observed atmospheric and oceanic spectra.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , R7
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bal, G., Komorowski, T. & Ryzhik, L. 2010 Kinetic limits for waves in a random medium. Kinet. Relat. Models 3, 529–644.Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.Google Scholar
Bühler, O., Callies, J. & Ferrari, R. 2014 Wave–vortex decomposition of one-dimensional ship-track data. J. Fluid Mech. 756, 1007–1026.Google Scholar
Callies, J., Bühler, O. & Ferrari, R. 2016 The dynamics of mesoscale winds in the upper troposphere and lower stratosphere. J. Atmos. Sci. 73, 4853–4872.Google Scholar
Callies, J. & Ferrari, R. 2013 Interpreting energy and tracer spectra of upper-ocean turbulence in the submesoscale range (1–200 km). J. Phys. Oceanogr. 43, 2456–2474.Google Scholar
Callies, J., Ferrari, R. & Bühler, O. 2014 Transition from geostrophic turbulence to inertia-gravity waves in the atmospheric energy spectrum. Proc. Natl Acad. Sci. USA 111, 17033–17038.Google Scholar
Danioux, E. & Vanneste, J. 2016 Propagation of near-inertial waves in random flows. Phys. Rev. Fluids 1, 0033701.Google Scholar
DLMF2018 NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, Release 1.0.21 of 2018-12-15 (ed. F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller and B. V. Saunders).Google Scholar
Garrett, C. J. & Munk, W. 1972 Space–time scales of internal waves. Geophys. Fluid Dyn. 2, 255–264.Google Scholar
Henyey, F. S. & Pomphrey, N. 1983 Eikonal description of internal wave interactions: non-diffusive picture of ‘induced diffusion’. Dyn. Atmos. Oceans 7, 189–219.Google Scholar
Kafiabad, H. A. & Bartello, P. 2018 Spontaneous imbalance in the non-hydrostatic Boussinesq equations. J. Fluid Mech. 847, 614–643.Google Scholar
Lelong, M.-P. & Riley, J. J. 1991 Internal wave-vortical mode interactions in strongly stratified flows. J. Fluid Mech. 232, 1–19.Google Scholar
Li, Q. & Linborg, E. 2018 Weakly or strongly nonlinear mesoscale dynamics close to the tropopause? J. Atmos. Sci. 94, 177–220.Google Scholar
Lvov, Y. V., Polzin, K. L. & Yokoyama, N. 2012 Resonant and near-resonant internal wave interactions. J. Phys. Oceanogr. 42, 669–691.Google Scholar
MacKinnon, J. A. & Winters, K. B. 2005 Subtropical catastrophe: significant loss of low-mode tidal energy at 28. 9° . Geophys. Res. Lett. 32 (15), L15605.Google Scholar
McComas, C. H. & Bretherton, F. P. 1977 Nonlinear interactions of internal gravity waves. J. Geophys. Res. 82, 1397–1412.Google Scholar
Müller, P. 1976 On the diffusion of mass and momentum by internal gravity waves. J. Fluid Mech. 77, 789–823.Google Scholar
Müller, P. 1977 Spectral features of the energy transfers between a larger-scale shear flow. Dyn. Atmos. Oceans 2, 49–72.Google Scholar
Müller, P., Holloway, G., Henyey, F. & Pomphrey, N. 1986 Nonlinear interactions among internal gravity waves. Rev. Geophys. 24, 493–536.Google Scholar
Müller, P. & Olbers, D. J. 1975 On the dynamics of internal waves in the deep ocean. J. Geophys. Res. 75, 3848–3860.Google Scholar
Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 42, 950–960.Google Scholar
Rocha, C. B., Chereskin, T. K. & Gille, S. T. 2016 Mesoscale to submesoscale wavenumber spectra in Drake Passage. J. Phys. Oceanogr. 46, 601–620.Google Scholar
Savva, M. A. C. & Vanneste, J. 2018 Scattering of internal tides by barotropic quasigeostrophic flows. J. Fluid Mech. 856, 504–530.Google Scholar
Waite, M. L. 2017 Random forcing of geostrophic motion in rotating stratified turbulence. Phys. Fluids 29, 126602.Google Scholar
Waite, M. L. & Bartello, P. 2006a Stratified turbulence generated by internal gravity waves. J. Fluid Mech. 546, 313–339.Google Scholar
Waite, M. L. & Bartello, P. 2006b The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.Google Scholar
Ward, M. L. & Dewar, W. K. 2010 Scattering of gravity waves by potential vorticity in a shallow-water fluid. J. Fluid Mech. 663, 478–506.Google Scholar