Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T05:13:12.277Z Has data issue: false hasContentIssue false
  • English
  • Français

Diapycnal mixing of passive tracers by Kelvin–Helmholtz instabilities

Published online by Cambridge University Press:  11 August 2020

Jared Penney Open the ORCID record for Jared Penney [Opens in a new window] ,
Yves Morel Open the ORCID record for Yves Morel [Opens in a new window] ,
Peter Haynes Open the ORCID record for Peter Haynes [Opens in a new window] ,
Francis Auclair Open the ORCID record for Francis Auclair [Opens in a new window]  and
Cyril Nguyen Open the ORCID record for Cyril Nguyen [Opens in a new window]
Jared Penney*
Affiliation:
LEGOS, Université de Toulouse, CNES, CNRS, IRD, UPS, Toulouse31400, France
Yves Morel
Affiliation:
LEGOS, Université de Toulouse, CNES, CNRS, IRD, UPS, Toulouse31400, France
Peter Haynes
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, CambridgeCB3 0WA, UK
Francis Auclair
Affiliation:
Laboratoire d'Aérologie, Université de Toulouse, CNRS, UPS, Toulouse31400, France
Cyril Nguyen
Affiliation:
Laboratoire d'Aérologie, Université de Toulouse, CNRS, UPS, Toulouse31400, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

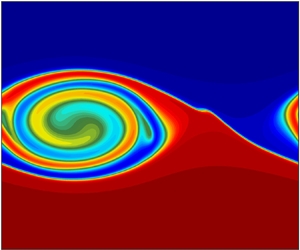
This paper considers the diapycnal transport of passive tracers during a Kelvin–Helmholtz mixing event. Numerical simulations of a traditional Kelvin–Helmholtz (KH) configuration of a stratified shear flow are extended to include layers of passive tracer at different locations relative to the shear layer. The evolution of the tracers during the simulation is followed and is analysed using different theoretical approaches. One is to consider the evolution via the distribution in density–tracer space which clearly reveals how the tracers are redistributed across isopycnals by the mixing driven by the growing and saturating KH billow. The shape of the distribution places constraints on the redistribution of the tracer and, for this problem of symmetrically stratified shear, it is shown that the distribution typically tends to a compact form, with significant regions that are nearly linear. The redistribution across isopycnals is also considered via a diffusion equation for the tracer relative to coordinates based on the geometry of density surfaces. The equation is a generalisation of an equation previously derived for transport of density in these coordinates and includes an extra eddy term that arises because there is variation of the tracer along density surfaces. Under certain circumstances and at later stages of the flow, the eddy term can be neglected, and the evolution of the mean tracer profile can be adequately represented using a simple diffusion equation where diffusivity is defined as the effective diffusivity of density, scaled by the molecular diffusion of the tracer.

JFM classification

Turbulent Flows: Stratified turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 900 , 10 October 2020 , A26
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alexakis, A. 2009 Stratified shear flow instabilities at large Richardson numbers. Phys. Fluids 21 (5), 054108.CrossRefGoogle Scholar
Auclair, F., Bordois, L., Dossmann, Y., Duhaut, T., Paci, A., Ulses, C. & Nguyen, C. 2018 A non-hydrostatic non-Boussinesq algorithm for free-surface ocean modelling. Ocean Model. 132, 12–29.CrossRefGoogle Scholar
Brierley, A. S. & Kingsford, M. J. 2009 Impacts of climate change on marine organisms and ecosystems. Curr. Biol. 19 (14), R602–R614.CrossRefGoogle ScholarPubMed
Browning, K. A. & Watkins, C. D. 1970 Observations of clear air turbulence by high power radar. Nature 227 (5255), 260–263.CrossRefGoogle ScholarPubMed
Butchart, N. & Remsberg, E. E. 1986 The area of the stratospheric polar vortex as a diagnostic for tracer transport on an isentropic surface. J. Atmos. Sci. 43 (13), 1319–1339.2.0.CO;2>CrossRefGoogle Scholar
Canuto, V. M., Cheng, Y. & Howard, A. M. 2011 Vertical diffusivities of active and passive tracers. Ocean Model. 36 (3), 198–207.CrossRefGoogle Scholar
Carpenter, J. R., Balmforth, N. J. & Lawrence, G. A. 2010 Identifying unstable modes in stratified shear layers. Phys. Fluids 22 (5), 054104.CrossRefGoogle Scholar
Caulfield, C. P. & Peltier, W. R. 1994 Three dimensionalization of the stratified mixing layer. Phys. Fluids 6 (12), 3803–3805.CrossRefGoogle Scholar
Caulfield, C. P., Yoshida, S. & Peltier, W. R. 1996 Secondary instability and three-dimensionalization in a laboratory accelerating shear layer with varying density differences. Dyn. Atmos. Oceans 23 (1), 125–138.CrossRefGoogle Scholar
Debreu, L., Marchesiello, P., Penven, P. & Cambon, G. 2012 Two-way nesting in split-explicit ocean models: algorithms, implementation and validation. Ocean Model. 49-50, 1–21.CrossRefGoogle Scholar
Fritts, D. C. & Rastogi, P. K. 1985 Convective and dynamical instabilities due to gravity wave motions in the lower and middle atmosphere: theory and observations. Radio Sci. 20 (6), 1247–1277.CrossRefGoogle Scholar
Fukao, S., Yamanaka, M. D., Ao, N., Hocking, W. K., Sato, T., Yamamoto, M., Nakamura, T., Tsuda, T. & Kato, S. 1994 Seasonal variability of vertical eddy diffusivity in the middle atmosphere: Part 1. Three-year observations by the middle and upper atmosphere radar. J. Geophys. Res. 99 (D9), 18973–18987.CrossRefGoogle Scholar
Geyer, W. R., Lavery, A. C., Scully, M. E. & Trowbridge, J. H. 2010 Mixing by shear instability at high Reynolds number. Geophys. Res. Lett. 37 (22), L22607.CrossRefGoogle Scholar
Geyer, W. R. & Smith, J. D. 1987 Shear instability in a highly stratified estuary. J. Phys. Oceanogr. 17 (10), 1668–1679.2.0.CO;2>CrossRefGoogle Scholar
Griffies, S. M. 2004 Fundamentals of Ocean Climate Models. Princeton University Press.Google Scholar
van Haren, H., Gostiaux, L. 2010 A deep-ocean Kelvin–Helmholtz billow train. Geophys. Res. Lett. 37 (3), L03605.CrossRefGoogle Scholar
Janjic, Z. I., Gerrity, J. P. & Nickovic, S. 2001 An alternative approach to nonhydrostatic modeling. Mon. Weath. Rev. 129 (5), 1164–1178.2.0.CO;2>CrossRefGoogle Scholar
Jiang, N. 2019 A pressure-correction ensemble scheme for computing evolutionary Boussinesq equations. J. Sci. Comput. 80 (1), 315–350.CrossRefGoogle Scholar
Klaassen, G. P. & Peltier, W. R. 1985 The onset of turbulence in finite-amplitude Kelvin–Helmholtz billows. J. Fluid Mech. 155, 1–35.CrossRefGoogle Scholar
Klaassen, G. P. & Peltier, W. R. 1989 The role of transverse secondary instabilities in the evolution of free shear layers. J. Fluid Mech. 202, 367–402.CrossRefGoogle Scholar
Lauritzen, P. H. & Thuburn, J. 2012 Evaluating advection/transport schemes using interrelated tracers, scatter plots and numerical mixing diagnostics. Q. J. R. Meteorol. Soc. 138 (665), 906–918.CrossRefGoogle Scholar
Ledwell, J. R., Watson, A. J. & Law, C. S. 1993 Evidence for slow mixing across the pycnocline from an open-ocean tracer-release experiment. Nature 364 (6439), 701.CrossRefGoogle Scholar
Li, D., Bou-Zeid, E. & De Bruin, H. A. R. 2012 Monin–Obukhov similarity functions for the structure parameters of temperature and humidity. Boundary-Layer Meteorol. 145 (1), 45–67.CrossRefGoogle Scholar
Lincoln, B. J., Rippeth, T. P. & Simpson, J. H. 2016 Surface mixed layer deepening through wind shear alignment in a seasonally stratified shallow sea. J. Geophys. Res. 121 (8), 6021–6034.CrossRefGoogle Scholar
Loder, T. C. & Reichard, R. P. 1981 The dynamics of conservative mixing in estuaries. Estuaries 4 (1), 64–69.CrossRefGoogle Scholar
Marmorino, G. O. 1987 Observations of small-scale mixing processes in the seasonal thermocline, part II: Wave breaking. J. Phys. Oceanogr. 17, 1348–1355.2.0.CO;2>CrossRefGoogle Scholar
Mashayek, A. & Peltier, W. R. 2012 a The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 1. Shear aligned convection, pairing, and braid instabilities. J. Fluid Mech. 708, 5–44.CrossRefGoogle Scholar
Mashayek, A. & Peltier, W. R. 2012 b The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 2. The influence of stratification. J. Fluid Mech. 708, 45–70.CrossRefGoogle Scholar
Mashayek, A. & Peltier, W. R. 2013 Shear-induced mixing in geophysical flows: does the route to turbulence matter to its efficiency? J. Fluid Mech. 725, 216–261.CrossRefGoogle Scholar
Nagata, K. & Komori, S. 2001 The difference in turbulent diffusion between active and passive scalars in stable thermal stratification. J. Fluid Mech. 430, 361–380.CrossRefGoogle Scholar
Nakamura, N. 1995 Modified Lagrangian-mean diagnostics of the stratospheric polar vortices. Part 1. Formulation and analysis of GFDL SKYHI GCM. J. Atmos. Sci. 52 (11), 2096–2108.2.0.CO;2>CrossRefGoogle Scholar
Nakamura, N. 1996 Two-dimensional mixing, edge formation, and permeability diagnosed in an area coordinate. J. Atmos. Sci. 53 (11), 1524–1537.2.0.CO;2>CrossRefGoogle Scholar
Officer, C. B. & Lynch, D. R. 1981 Dynamics of mixing in estuaries. Estuar. Coast. Shelf Sci. 12 (5), 525–533.CrossRefGoogle Scholar
Patterson, M. D., Caulfield, C. P., McElwaine, J. N. & Dalziel, S. B. 2006 Time-dependent mixing in stratified Kelvin–Helmholtz billows: experimental observations. Geophys. Res. Lett. 33 (15), L15608.CrossRefGoogle Scholar
Penney, J. & Stastna, M. 2016 Direct numerical simulation of double-diffusive gravity currents. Phys. Fluids 28 (8), 086602.CrossRefGoogle Scholar
Plumb, R. A. 2007 Tracer interrelationships in the stratosphere. Rev. Geophys. 45 (4), RG4005.CrossRefGoogle Scholar
Rhines, P. B. & Young, W. R. 1983 How rapidly is a passive scalar mixed within closed streamlines? J. Fluid Mech. 133, 133–145.CrossRefGoogle Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.CrossRefGoogle Scholar
Salehipour, H., Peltier, W. R. & Mashayek, A. 2015 Turbulent diapycnal mixing in stratified shear flows: the influence of Prandtl number on mixing efficiency and transition at high Reynolds number. J. Fluid Mech. 773, 178–223.CrossRefGoogle Scholar
Scinocca, J. F. 1995 The mixing of mass and momentum by Kelvin–Helmboltz billows. J. Atmos. Sci. 52 (14), 2509–2530.2.0.CO;2>CrossRefGoogle Scholar
Seinfeld, J. H. & Pandis, S. N. 1998 Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. John Wiley & Sons.Google Scholar
Shchepetkin, A. F. & McWilliams, J. C. 2005 The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 9 (4), 347–404.CrossRefGoogle Scholar
Shete, M. H. & Guha, A. 2018 Effect of free surface on submerged stratified shear instabilities. J. Fluid Mech. 843, 98–125.CrossRefGoogle Scholar
Shu, C.-W. 1999 High order ENO and WENO schemes for computational fluid dynamics. In High-Order Methods for Computational Physics (ed. Barth, T. J. & Deconinck, H.), pp. 439–582. Springer.CrossRefGoogle Scholar
Shuckburgh, E. & Haynes, P. 2003 Diagnosing transport and mixing using a tracer-based coordinate system. Phys. Fluids 15 (11), 3342–3357.CrossRefGoogle Scholar
Smyth, W. D. & Moum, J. N. 2012 Ocean mixing by Kelvin–Helmholtz instability. Oceanography 25 (2), 140–149.CrossRefGoogle Scholar
Smyth, W. D., Nash, J. D. & Moum, J. N. 2005 Differential diffusion in breaking Kelvin–Helmholtz billows. J. Phys. Oceanogr. 35 (6), 1004–1022.CrossRefGoogle Scholar
Sparling, L. C., Kettleborough, J. A., Haynes, P. H., McIntyre, M. E., Rosenfield, J. E., Schoeberl, M. R. & Newman, P. A. 1997 Diabatic cross-isentropic dispersion in the lower stratosphere. J. Geophys. Res. 102 (D22), 25817–25829.CrossRefGoogle Scholar
Subich, C. J., Lamb, K. G. & Stastna, M. 2013 Simulation of the Navier–Stokes equations in three dimensions with a spectral collocation method. Intl J. Numer. Meth. Fluids 73 (2), 103–129.CrossRefGoogle Scholar
Tailleux, R. 2009 On the energetics of stratified turbulent mixing, irreversible thermodynamics, Boussinesq models and the ocean heat engine controversy. J. Fluid Mech. 638, 339–382.CrossRefGoogle Scholar
Teramoto, T. 1993 Deep Ocean Circulation: Physical and Chemical Aspects. Elsevier.Google Scholar
Thorpe, S. A. 1973 Experiments on instability and turbulence in a stratified shear flow. J. Fluid Mech. 61 (4), 731–751.CrossRefGoogle Scholar
Tilmes, S., Müller, R., Grooß, J.-U., Nakajima, H. & Sasano, Y. 2006 Development of tracer relations and chemical ozone loss during the setup phase of the polar vortex. J. Geophys. Res. 111 (D24), D24S90.CrossRefGoogle Scholar
Tomczak, M. 1981 A multi-parameter extension of temperature/salinity diagram techniques for the analysis of non-isopycnal mixing. Prog. Oceanogr. 10 (3), 147–171.CrossRefGoogle Scholar
Vaquer-Sunyer, R. & Duarte, C. M. 2008 Thresholds of hypoxia for marine biodiversity. Proc. Natl Acad. Sci. 105 (40), 15452–15457.CrossRefGoogle ScholarPubMed
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.CrossRefGoogle Scholar
Winters, K. B. & D'Asaro, E. A. 1996 Diascalar flux and the rate of fluid mixing. J. Fluid Mech. 317, 179–193.CrossRefGoogle Scholar
Woods, J. D. 1968 Wave-induced shear instability in the summer thermocline. J. Fluid Mech. 32 (4), 791–800.CrossRefGoogle Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36 (1), 281–314.CrossRefGoogle Scholar
Yang, Q., Easter, R. C., Campuzano-Jost, P., Jimenez, J. L., Fast, J. D., Ghan, S. J., Wang, H., Berg, L. K., Barth, M. C., Liu, Y., et al. . 2015 Aerosol transport and wet scavenging in deep convective clouds: a case study and model evaluation using a multiple passive tracer analysis approach. J. Geophys. Res. 120 (16), 8448–8468.Google Scholar
Zhou, Q., Taylor, J. R., Caulfield, C. P. & Linden, P. F. 2017 Diapycnal mixing in layered stratified plane Couette flow quantified in a tracer-based coordinate. J. Fluid Mech. 823, 198–229.CrossRefGoogle Scholar