Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T19:08:10.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Destabilization of a stratified shear layer by ambient turbulence

Published online by Cambridge University Press:  14 April 2015

Lin Li ,
W. D. Smyth  and
S. A. Thorpe
Lin Li*
Affiliation:
College of Earth, Ocean and Atmospheric Sciences, Oregon State University, Corvallis, OR 97331, USA
W. D. Smyth
Affiliation:
College of Earth, Ocean and Atmospheric Sciences, Oregon State University, Corvallis, OR 97331, USA
S. A. Thorpe
Affiliation:
School of Ocean Sciences, Bangor University, Menai Bridge, Anglesey LL59 5AB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A small eddy viscosity or mass diffusivity that varies with height has been found to have unexpected effects on the Kelvin–Helmholtz (KH) instability of a stably stratified shear layer near the neutral stability boundary. In particular, varying viscosity can increase the growth rate of the instability in contrast to the effect of uniform viscosity. Here, these results are extended to parameter ranges relevant in many geophysical and engineering contexts. We find that linearization of the viscous terms based on the assumption of weak viscosity/diffusivity is valid for non-dimensional values (inverse Reynolds number) up to 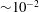${\sim}10^{-2}$. Decreasing the Richardson number far below its critical value 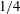$1/4$ can change, or even reverse, the effects of eddy viscosity and diffusivity. A primary goal is to explain the unexpected destabilization by viscosity. Varying viscosity affects vorticity (and other fluid properties) in a manner identical to advection with an advecting velocity equal to minus the gradient of viscosity. Destabilization occurs when this viscous ‘advection’ reinforces the vorticity distribution of a growing mode.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Instability: Instability Turbulent Flows: Shear layer turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 771 , 25 May 2015 , pp. 1 - 15
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G. & Mitsudera, H. 1994 On the mechanism of shear flow instabilities. J. Fluid Mech. 276, 327–342.Google Scholar
Betchov, R. & Szewczyk, A. 1963 Stability of a shear layer between parallel streams. Phys. Fluids 6, 1391–1396.Google Scholar
Brucker, K. & Sarkar, S. 2007 Evolution of an initially turbulent stratified shear layer. Phys. Fluids 19, 105105.Google Scholar
Carpenter, J. R., Tedford, E. W., Heifitz, E. & Lawrence, G. A. 2013 Instability in stratified shear flow: review of a physical interpretation based on interacting waves. Appl. Mech. Rev. 64 (6), 060801, 1–17.Google Scholar
Corcos, G. M. & Sherman, F. S. 1976 Vorticity concentration and the dynamics of unstable free shear layers. J. Fluid Mech. 73, 241–264.CrossRefGoogle Scholar
Defina, A., Lanzoni, S. & Susin, F. M. 1999 Stability of a stratified viscous shear flow in a tilted tube. Phys. Fluids 11, 344–355.Google Scholar
Gregg, M. C. & Sanford, T. B. 1987 Shear and turbulence in thermohaline staircases. Deep-Sea Res. 34, 689–1696.Google Scholar
Kimura, S., Smyth, W. D. & Kunze, E. 2011 Sheared, double-diffusive turbulence: anisotropy and effective diffusivities. J. Phys. Oceanogr. 41, 1144–1159.CrossRefGoogle Scholar
Liu, Z., Thorpe, S. A. & Smyth, W. D. 2012 Instability and hydraulics of turbulent stratified shear flows. J. Fluid Mech. 695, 235–256.Google Scholar
Maslowe, S. A. & Thompson, J. M. 1971 Stability of a stratified free shear layer. Phys. Fluids 14, 453–458.Google Scholar
Phillips, O. M. 1972 Turbulence in a strongly stratified fluid: is it unstable? Deep-Sea Res. 19, 79–81.Google Scholar
Posmentier, E. S. 1977 The generation of salinity finestructure by vertical diffusion. J. Phys. Oceanogr. 7, 298–300.Google Scholar
Rayleigh, L. 1880 On the stability or instability of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–70.Google Scholar
Smyth, W. D. 2003 Secondary Kelvin–Helmholtz instability in a weakly stratified shear flow. J. Fluid Mech. 497, 67–98.Google Scholar
Smyth, W. D., Klaassen, G. P. & Peltier, W. R. 1988 Finite amplitude Holmboe waves. Geophys. Astrophys. Fluid Dyn. 43, 181–222.Google Scholar
Smyth, W. D. & Moum, J. N. 2012 Ocean mixing by Kelvin–Helmholtz instability. Oceanography 25 (2), 140–149.Google Scholar
Smyth, W. D. & Moum, J. N. 2013 Marginal instability and deep cycle turbulence in the eastern equatorial Pacific ocean. Geophys. Res. Lett. 40, 6181–6185.Google Scholar
Smyth, W. D., Moum, J. N. & Li, L. 2013 Diurnal shear instability, the descent of the surface shear layer, and the deep cycle of equatorial turbulence. J. Phys. Oceanogr. 43, 2432–2455.Google Scholar
Smyth, W. D. & Peltier, W. R. 1989 The transition between Kelvin–Helmholtz and Holmboe instability: an investigation of the overreflecion hypothesis. J. Atmos. Sci. 46, 3698–3720.Google Scholar
Staquet, C. 1995 Two-dimensional secondary instabilities in a strongly stratified shear layer. J. Fluid Mech. 296, 73–126.Google Scholar
Thorpe, S. A. & Liu, Z. 2009 Marginal instability? J. Phys. Oceanogr. 39, 2373–2381.Google Scholar
Thorpe, S. A., Smyth, W. D. & Li, L. 2013 The effect of small viscosity and diffusivity on the marginal stability of stably stratified shear flows. J. Fluid Mech. 731, 461–476.Google Scholar