Article contents
A depth-averaged 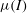 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu (I)$-rheology for shallow granular free-surface flows
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu (I)$-rheology for shallow granular free-surface flows
Published online by Cambridge University Press: 20 August 2014
Abstract
The 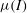 $\mu (I)$-rheology is a nonlinear viscous law, with a strain-rate invariant and pressure-dependent viscosity, that has proved to be effective at modelling dry granular flows in the intermediate range of the inertial number,
$\mu (I)$-rheology is a nonlinear viscous law, with a strain-rate invariant and pressure-dependent viscosity, that has proved to be effective at modelling dry granular flows in the intermediate range of the inertial number, 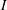 $I$. This paper shows how to incorporate the rheology into depth-averaged granular avalanche models. To leading order, the rheology generates an effective basal friction, which is equivalent to a rough bed friction law. A depth-averaged viscous-like term can be derived by integrating the in-plane deviatoric stress through the avalanche depth, using pressure and velocity profiles from a steady-uniform solution to the full
$I$. This paper shows how to incorporate the rheology into depth-averaged granular avalanche models. To leading order, the rheology generates an effective basal friction, which is equivalent to a rough bed friction law. A depth-averaged viscous-like term can be derived by integrating the in-plane deviatoric stress through the avalanche depth, using pressure and velocity profiles from a steady-uniform solution to the full 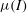 $\mu (I)$-rheology. The resulting viscosity is proportional to the thickness to the three halves power, with a coefficient of proportionality that is angle dependent. When substituted into the depth-averaged momentum balance this term generates second-order derivatives of the depth-averaged velocity, which are multiplied by a small parameter. Its inclusion therefore represents a singular perturbation to the equations. It is shown that a granular front propagating down a rough inclined plane is completely unaffected by the rheology, but, discontinuities, which naturally develop in inviscid roll-wave solutions, are smoothed out. By comparison with existing experimental data, it is shown that the depth-averaged
$\mu (I)$-rheology. The resulting viscosity is proportional to the thickness to the three halves power, with a coefficient of proportionality that is angle dependent. When substituted into the depth-averaged momentum balance this term generates second-order derivatives of the depth-averaged velocity, which are multiplied by a small parameter. Its inclusion therefore represents a singular perturbation to the equations. It is shown that a granular front propagating down a rough inclined plane is completely unaffected by the rheology, but, discontinuities, which naturally develop in inviscid roll-wave solutions, are smoothed out. By comparison with existing experimental data, it is shown that the depth-averaged 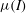 $\mu (I)$-rheology accurately predicts the growth rate of spatial instabilities to steady-uniform flow, as well as the dependence of the cutoff frequency on the Froude number and inclination angle. This provides strong evidence that, in the steady-uniform flow regime, the predicted decrease in the viscosity with increasing slope is correct. Outside the range of angles where steady-uniform flows develop, the viscosity becomes negative, which implies that the equations are ill-posed. This is a signature of the ill-posedness of the full
$\mu (I)$-rheology accurately predicts the growth rate of spatial instabilities to steady-uniform flow, as well as the dependence of the cutoff frequency on the Froude number and inclination angle. This provides strong evidence that, in the steady-uniform flow regime, the predicted decrease in the viscosity with increasing slope is correct. Outside the range of angles where steady-uniform flows develop, the viscosity becomes negative, which implies that the equations are ill-posed. This is a signature of the ill-posedness of the full 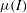 $\mu (I)$-rheology at both high and low inertial numbers. The depth-averaged
$\mu (I)$-rheology at both high and low inertial numbers. The depth-averaged 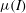 $\mu (I)$-rheology therefore cannot be used outside the valid range of angles without additional regularization.
$\mu (I)$-rheology therefore cannot be used outside the valid range of angles without additional regularization.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 169
- Cited by


