Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhu, LaiLai
Rabault, Jean
and
Brandt, Luca
2015.
The dynamics of a capsule in a wall-bounded oscillating shear flow.
Physics of Fluids,
Vol. 27,
Issue. 7,
Cordasco, Daniel
and
Bagchi, Prosenjit
2016.
Dynamics of red blood cells in oscillating shear flow.
Journal of Fluid Mechanics,
Vol. 800,
Issue. ,
p.
484.
Barthès-Biesel, Dominique
2016.
Motion and Deformation of Elastic Capsules and Vesicles in Flow.
Annual Review of Fluid Mechanics,
Vol. 48,
Issue. 1,
p.
25.
Ishida, Shunichi
Imai, Yohsuke
Ichikawa, Yuki
Nix, Stephanie
Matsunaga, Daiki
Omori, Toshihiro
and
Ishikawa, Takuji
2016.
A numerical model of a red blood cell infected by Plasmodium falciparum malaria: coupling cell mechanics with ligand-receptor interactions.
Science and Technology of Advanced Materials,
Vol. 17,
Issue. 1,
p.
454.
Matsunaga, D.
Imai, Y.
Wagner, C.
and
Ishikawa, T.
2016.
Reorientation of a single red blood cell during sedimentation.
Journal of Fluid Mechanics,
Vol. 806,
Issue. ,
p.
102.
Imai, Yohsuke
Omori, Toshihiro
Shimogonya, Yuji
Yamaguchi, Takami
and
Ishikawa, Takuji
2016.
Numerical methods for simulating blood flow at macro, micro, and multi scales.
Journal of Biomechanics,
Vol. 49,
Issue. 11,
p.
2221.
Laumann, M.
Bauknecht, P.
Gekle, S.
Kienle, D.
and
Zimmermann, W.
2017.
Cross-stream migration of asymmetric particles driven by oscillating shear.
EPL (Europhysics Letters),
Vol. 117,
Issue. 4,
p.
44001.
Guckenberger, Achim
and
Gekle, Stephan
2017.
Theory and algorithms to compute Helfrich bending forces: a review.
Journal of Physics: Condensed Matter,
Vol. 29,
Issue. 20,
p.
203001.
Boujja, Zakaria
Misbah, Chaouqi
Ez-Zahraouy, Hamid
Benyoussef, Abdelilah
John, Thomas
Wagner, Christian
and
Müller, Martin Michael
2018.
Vesicle dynamics in confined steady and harmonically modulated Poiseuille flows.
Physical Review E,
Vol. 98,
Issue. 4,
Luo, Zheng Yuan
and
Bai, Bo Feng
2018.
Dynamics of capsules enclosing viscoelastic fluid in simple shear flow.
Journal of Fluid Mechanics,
Vol. 840,
Issue. ,
p.
656.
Li, He
Papageorgiou, Dimitrios P.
Chang, Hung-Yu
Lu, Lu
Yang, Jun
and
Deng, Yixiang
2018.
Synergistic Integration of Laboratory and Numerical Approaches in Studies of the Biomechanics of Diseased Red Blood Cells.
Biosensors,
Vol. 8,
Issue. 3,
p.
76.
Imai, Yohsuke
and
Matsunaga, Daiki
2018.
Frontiers in Computational Fluid-Structure Interaction and Flow Simulation.
p.
213.
2018.
Integrated Nano-Biomechanics.
p.
9.
Owen, Benjamin
Bojdo, Nicholas
Jivkov, Andrey
Keavney, Bernard
and
Revell, Alistair
2018.
Structural modelling of the cardiovascular system.
Biomechanics and Modeling in Mechanobiology,
Vol. 17,
Issue. 5,
p.
1217.
Coclite, Alessandro
and
Gambaruto, Alberto M.
2019.
Injection of Deformable Capsules in a Reservoir: A Systematic Analysis.
Fluids,
Vol. 4,
Issue. 3,
p.
122.
Maestre, Jorge
Pallares, Jordi
Cuesta, Ildefonso
and
Scott, Michael A.
2019.
Dynamics of a capsule flowing in a tube under pulsatile flow.
Journal of the Mechanical Behavior of Biomedical Materials,
Vol. 90,
Issue. ,
p.
441.
Zhang, Yuling
Han, Yunlong
Zhang, Lili
Chen, Qiaoyue
Ding, Mingming
and
Shi, Tongfei
2020.
Dynamic mode of viscoelastic capsules in steady and oscillating shear flow.
Physics of Fluids,
Vol. 32,
Issue. 10,
Lafzi, Ali
Raffiee, Amir Hossein
and
Dabiri, Sadegh
2020.
Inertial migration of a deformable capsule in an oscillatory flow in a microchannel.
Physical Review E,
Vol. 102,
Issue. 6,
Jaensson, Nick O.
Anderson, Patrick D.
and
Vermant, Jan
2021.
Computational interfacial rheology.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 290,
Issue. ,
p.
104507.
Liu, Haihu
Lu, Yang
Li, Sheng
Yu, Yuan
and
Sahu, Kirti Chandra
2021.
Deformation and breakup of a compound droplet in three-dimensional oscillatory shear flow.
International Journal of Multiphase Flow,
Vol. 134,
Issue. ,
p.
103472.
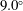 $9.0^{\circ }$. We propose an equation to estimate the threshold frequency between the low-frequency range, where the capsule may have an overshoot, and the high-frequency range, where the deformation is given by the leading-order prediction. The equation only includes the viscosity ratio and the Taylor parameter under simple shear flow, so it can be extended to other deformable particles, such as bubbles and drops.
$9.0^{\circ }$. We propose an equation to estimate the threshold frequency between the low-frequency range, where the capsule may have an overshoot, and the high-frequency range, where the deformation is given by the leading-order prediction. The equation only includes the viscosity ratio and the Taylor parameter under simple shear flow, so it can be extended to other deformable particles, such as bubbles and drops.