Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Karyappa, Rahul B.
Deshmukh, Shivraj D.
and
Thaokar, Rochish M.
2014.
Breakup of a conducting drop in a uniform electric field.
Journal of Fluid Mechanics,
Vol. 754,
Issue. ,
p.
550.
Zabarankin, Michael
Lavrenteva, Olga M.
and
Nir, Avinoam
2015.
Liquid toroidal drop in compressional Stokes flow.
Journal of Fluid Mechanics,
Vol. 785,
Issue. ,
p.
372.
Das, Sudip
Mayya, Y. S.
and
Thaokar, Rochish
2015.
Dynamics of a charged drop in a quadrupole electric field.
EPL (Europhysics Letters),
Vol. 111,
Issue. 2,
p.
24006.
Mandal, Shubhadeep
Bandopadhyay, Aditya
and
Chakraborty, Suman
2016.
Effect of surface charge convection and shape deformation on the dielectrophoretic motion of a liquid drop.
Physical Review E,
Vol. 93,
Issue. 4,
Bandopadhyay, Aditya
Mandal, Shubhadeep
Kishore, N. K.
and
Chakraborty, Suman
2016.
Uniform electric-field-induced lateral migration of a sedimenting drop.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
553.
Mandal, Shubhadeep
Bandopadhyay, Aditya
and
Chakraborty, Suman
2016.
The effect of uniform electric field on the cross-stream migration of a drop in plane Poiseuille flow.
Journal of Fluid Mechanics,
Vol. 809,
Issue. ,
p.
726.
Zabarankin, Michael
2016.
Liquid toroidal drop in compressional flow with arbitrary drop-to-ambient fluid viscosity ratio.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 472,
Issue. 2187,
p.
20150737.
Mandal, Shubhadeep
and
Chakraborty, Suman
2017.
Influence of interfacial viscosity on the dielectrophoresis of drops.
Physics of Fluids,
Vol. 29,
Issue. 5,
Zabarankin, Michael
2017.
Toroidal drop under electric field: arbitrary drop-to-ambient fluid viscosity ratio.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 473,
Issue. 2205,
p.
20170379.
Mandal, Shubhadeep
Bandopadhyay, Aditya
and
Chakraborty, Suman
2017.
The effect of surface charge convection and shape deformation on the settling velocity of drops in nonuniform electric field.
Physics of Fluids,
Vol. 29,
Issue. 1,
Mandal, Shubhadeep
Chakrabarti, Suryapratim
and
Chakraborty, Suman
2017.
Effect of nonuniform electric field on the electrohydrodynamic motion of a drop in Poiseuille flow.
Physics of Fluids,
Vol. 29,
Issue. 5,
Zabarankin, Michael
2017.
Liquid toroidal drop under uniform electric field.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 473,
Issue. 2202,
p.
20160633.
Das, Sudip
and
Thaokar, Rochish M.
2018.
Large-deformation electrohydrodynamics of an elastic capsule in a DC electric field.
Journal of Fluid Mechanics,
Vol. 841,
Issue. ,
p.
489.
Ee, B. K.
Lavrenteva, O. M.
Smagin, I.
and
Nir, A.
2018.
Evolution and stationarity of liquid toroidal drop in compressional Stokes flow.
Journal of Fluid Mechanics,
Vol. 835,
Issue. ,
p.
1.
Wang, Yanning
Sun, Dongliang
Li, Yinshi
Chen, Shuai
and
Yu, Bo
2019.
Migration behaviors of leaky dielectric droplets with electric and hydrodynamic forces.
Physical Review E,
Vol. 100,
Issue. 3,
Sinha, Kumari Priti
and
Thaokar, Rochish M
2019.
Shape deformation of a vesicle under an axisymmetric non-uniform alternating electric field.
Journal of Physics: Condensed Matter,
Vol. 31,
Issue. 3,
p.
035101.
Zabarankin, Michael
2019.
Small Deformation Analysis for Stationary Toroidal Drops in a Compressional Flow.
SIAM Journal on Applied Mathematics,
Vol. 79,
Issue. 5,
p.
2150.
Vlahovska, Petia M.
2019.
Electrohydrodynamics of Drops and Vesicles.
Annual Review of Fluid Mechanics,
Vol. 51,
Issue. 1,
p.
305.
Sorgentone, Chiara
Tornberg, Anna-Karin
and
Vlahovska, Petia M.
2019.
A 3D boundary integral method for the electrohydrodynamics of surfactant-covered drops.
Journal of Computational Physics,
Vol. 389,
Issue. ,
p.
111.
Gawande, Neha
Mayya, Y. S.
and
Thaokar, Rochish
2020.
Jet and progeny formation in the Rayleigh breakup of a charged viscous drop.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
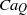 $C{a}_{Q} $, a ratio of electric to capillary stress) and numerical (boundary element) methods are used. A complete phase diagram for the drop deformation in the
$C{a}_{Q} $, a ratio of electric to capillary stress) and numerical (boundary element) methods are used. A complete phase diagram for the drop deformation in the 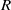 $R$–
$R$–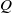 $Q$ plane is presented, where
$Q$ plane is presented, where 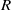 $R$ and
$R$ and 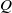 $Q$ are the non-dimensional ratios of the resistivities and dielectric constants, respectively, of the drop and the medium phase. The prolate and oblate deformations are mapped in the phase diagram, and the flow contours are also shown. The large deformation and breakup of a drop at higher
$Q$ are the non-dimensional ratios of the resistivities and dielectric constants, respectively, of the drop and the medium phase. The prolate and oblate deformations are mapped in the phase diagram, and the flow contours are also shown. The large deformation and breakup of a drop at higher 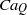 $C{a}_{Q} $ are analysed using the boundary element method. Several non-trivial shapes are observed at the onset of breakup of a drop. A prolate drop always breaks above a certain critical value of
$C{a}_{Q} $ are analysed using the boundary element method. Several non-trivial shapes are observed at the onset of breakup of a drop. A prolate drop always breaks above a certain critical value of 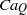 $C{a}_{Q} $. In the oblate deformation cases, breakup as well as steady shapes are observed at a higher value of
$C{a}_{Q} $. In the oblate deformation cases, breakup as well as steady shapes are observed at a higher value of 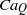 $C{a}_{Q} $. A detailed study of prolate and oblate deformation tendencies due to the normal and tangential electric stresses and the countervailing role of viscous stresses is presented. The circulation inside a drop is found to be more intense for a quadrupole field as compared with a uniform electric field. More intense internal circulations can lead to enhanced mixing characteristics and will have implications in microfluidic devices.
$C{a}_{Q} $. A detailed study of prolate and oblate deformation tendencies due to the normal and tangential electric stresses and the countervailing role of viscous stresses is presented. The circulation inside a drop is found to be more intense for a quadrupole field as compared with a uniform electric field. More intense internal circulations can lead to enhanced mixing characteristics and will have implications in microfluidic devices.