Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tajfirooz, S.
Meijer, J. G.
Kuerten, J. G. M.
Hausmann, M.
Fröhlich, J.
and
Zeegers, J. C. H.
2021.
Statistical-learning method for predicting hydrodynamic drag, lift, and pitching torque on spheroidal particles.
Physical Review E,
Vol. 103,
Issue. 2,
Kharrouba, Mohammed
Pierson, Jean-Lou
and
Magnaudet, Jacques
2021.
Flow structure and loads over inclined cylindrical rodlike particles and fibers.
Physical Review Fluids,
Vol. 6,
Issue. 4,
Jiang, F.
Zhao, L.
Andersson, H. I.
Gustavsson, K.
Pumir, A.
and
Mehlig, B.
2021.
Inertial torque on a small spheroid in a stationary uniform flow.
Physical Review Fluids,
Vol. 6,
Issue. 2,
Fröhlich, Konstantin
Farmand, Pooria
Pitsch, Heinz
Meinke, Matthias
and
Schröder, Wolfgang
2021.
Particle Reynolds number effects on settling ellipsoids in isotropic turbulence.
International Journal of Multiphase Flow,
Vol. 139,
Issue. ,
p.
103566.
Chen, Yong
Jiang, Pan
Xiong, Ting
Wei, Wei
Fang, Zhenlong
and
Wang, Bin
2021.
Drag and heat transfer coefficients for axisymmetric nonspherical particles: A LBM study.
Chemical Engineering Journal,
Vol. 424,
Issue. ,
p.
130391.
Sanjeevi, Sathish K.P.
Dietiker, Jean F.
and
Padding, Johan T.
2022.
Accurate hydrodynamic force and torque correlations for prolate spheroids from Stokes regime to high Reynolds numbers.
Chemical Engineering Journal,
Vol. 444,
Issue. ,
p.
136325.
Bhagat, Atul Manikrao
and
Goswami, Partha Sarathi
2022.
Effect of rough wall on drag, lift, and torque on an ellipsoidal particle in a linear shear flow.
Physics of Fluids,
Vol. 34,
Issue. 8,
Cabrera-Booman, F.
Sheikh, M. Z.
Mehlig, B.
Plihon, N.
Bourgoin, M.
Pumir, A.
and
Naso, A.
2022.
Experimental validation of fluid inertia models for a cylinder settling in a quiescent flow.
Physical Review Fluids,
Vol. 7,
Issue. 2,
Castang, C.
Laín, S.
García, D.
and
Sommerfeld, M.
2022.
Aerodynamic coefficients of irregular non-spherical particles at intermediate Reynolds numbers.
Powder Technology,
Vol. 402,
Issue. ,
p.
117341.
Cao, Ze
and
Tafti, Danesh K.
2022.
Characterization of lift force and torque in prolate ellipsoid suspensions.
Powder Technology,
Vol. 405,
Issue. ,
p.
117553.
Kiwitt, Thede
Fröhlich, Konstantin
Meinke, Matthias
and
Schröder, Wolfgang
2022.
Nusselt correlation for ellipsoidal particles.
International Journal of Multiphase Flow,
Vol. 149,
Issue. ,
p.
103941.
Michel, Antoine
and
Arcen, Boris
2023.
Translational and angular velocities statistics of inertial prolate ellipsoids in a turbulent channel flow up to Re
τ
= 1000.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Geschwindner, Christopher
Westrup, Katharina
Dreizler, Andreas
and
Böhm, Benjamin
2023.
Pulse picking of a fiber laser enables velocimetry of biomass-laden jets at low and ultra-high repetition rates.
Proceedings of the Combustion Institute,
Vol. 39,
Issue. 1,
p.
1325.
Li, Yansong
Xu, Chunxiao
and
Zhao, Lihao
2023.
Fluid-inertia torque on spheroids in pseudo-plastic fluid flows: effect of shear-thinning rheology.
Journal of Fluid Mechanics,
Vol. 970,
Issue. ,
Chouippe, Agathe
Kidanemariam, Aman G.
Derksen, Jos
Wachs, Anthony
and
Uhlmann, Markus
2023.
Modeling Approaches and Computational Methods for Particle-Laden Turbulent Flows.
p.
185.
Michaelides, Efstathios E.
and
Feng, Zhigang
2023.
Review—Drag Coefficients of Non-Spherical and Irregularly Shaped Particles.
Journal of Fluids Engineering,
Vol. 145,
Issue. 6,
Cui, Zhiwen
Qiu, Jingran
Jiang, Xinyu
and
Zhao, Lihao
2023.
Effect of fluid inertial torque on the rotational and orientational dynamics of tiny spheroidal particles in turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 977,
Issue. ,
Shu, Q.
Rietz, Manuel
Kneer, Reinhold
and
Rohlfs, Wilko
2023.
Thermal convection enhancement of laminar particle-laden flow in a square duct: fully resolved numerical investigation
.
p.
10.
Basit, Romana
Li, Xinyang
Huang, Zheqing
and
Zhou, Qiang
2023.
Effect of Particle Orientation on Heat Transfer in Arrays of Prolate Particles.
Computer Modeling in Engineering & Sciences,
Vol. 136,
Issue. 2,
p.
1509.
Saccone, D.
De Marchis, M.
Milici, B.
and
Marchioli, C.
2023.
Transport of inertial ellipsoidal particles in turbulent flow over rough walls.
Physical Review Fluids,
Vol. 8,
Issue. 8,
 $1 \leq Re \leq 100$, aspect ratios
$1 \leq Re \leq 100$, aspect ratios  $1 \leq \beta \leq 8$ and inclination angles
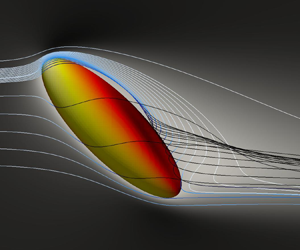
$1 \leq \beta \leq 8$ and inclination angles  $0^\circ \leq \phi \leq 90^\circ$ is covered by approximately 4400 simulations. Flow visualizations and skin friction distributions are presented for selected configurations. Aspect ratios
$0^\circ \leq \phi \leq 90^\circ$ is covered by approximately 4400 simulations. Flow visualizations and skin friction distributions are presented for selected configurations. Aspect ratios  $1\leq \beta \lesssim 3$ are identified as transitional geometries to fibres. For
$1\leq \beta \lesssim 3$ are identified as transitional geometries to fibres. For  $\beta \gtrsim 3$, the flow topology is qualitatively unaffected by higher aspect ratios. If the major axis is aligned with the free stream, i.e.
$\beta \gtrsim 3$, the flow topology is qualitatively unaffected by higher aspect ratios. If the major axis is aligned with the free stream, i.e.  $\phi = 0^\circ$, the ellipsoids are slender bodies, whereas for
$\phi = 0^\circ$, the ellipsoids are slender bodies, whereas for  $\phi = 90^\circ$ a bluff body flow is observed. Conditions for the onset of flow separation are reported. The data base is used to determine correlations for drag, lift and torque. The correlations are incorporated into dynamic equations for ellipsoidal Lagrangian models and limitations are discussed.
$\phi = 90^\circ$ a bluff body flow is observed. Conditions for the onset of flow separation are reported. The data base is used to determine correlations for drag, lift and torque. The correlations are incorporated into dynamic equations for ellipsoidal Lagrangian models and limitations are discussed.