Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-25T06:23:35.052Z Has data issue: false hasContentIssue false
  • English
  • Français

Corner separation effects for normal shock wave/turbulent boundary layer interactions in rectangular channels

Published online by Cambridge University Press:  02 August 2012

D. M. F. Burton  and
H. Babinsky
D. M. F. Burton
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
H. Babinsky*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

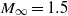Experiments are conducted to examine the mechanisms behind the coupling between corner separation and separation away from the corner when holding a high-Mach-number normal shock in a rectangular channel. The ensuing shock wave interaction with the boundary layer on the wind tunnel floor and in the corners was studied using laser Doppler anemometry, Pitot probe traverses, pressure sensitive paint and flow visualization. The primary mechanism explaining the link between the corner separation size and the other areas of separation appears to be the generation of compression waves at the corner, which act to smear the adverse pressure gradient imposed upon other parts of the flow. Experimental results indicate that the alteration of the 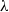-region, which occurs in the supersonic portion of the shock wave/boundary layer interaction (SBLI), is more important than the generation of any blockage in the subsonic region downstream of the shock wave.

JFM classification

Boundary Layers: Boundary layer separation Aerodynamics: High-speed flow Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 287 - 306
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bruce, P. J. K. & Babinsky, H. 2008 Unsteady shock wave dynamics. J. Fluid Mech. 603, 463–473.CrossRefGoogle Scholar
2. Bruce, P. J. K., Burton, D. M. F., Titchener, N. T. & Babinsky, H 2011 Corner effect and separation in transonic channel flows. J. Fluid Mech. 679, 247–262.CrossRefGoogle Scholar
3. Chriss, R. M., Keith, T. G. Jr., Hingst, W. R., Strazisar, A. J. & Porro, A. R. 1989 An LDA investigation of three-dimensional normal shock wave boundary-layer interactions. In NASA, Langley Research Center, Transonic Symposium: Theory, Application, and Experiment, vol 1, Part 2,. pp. 741–764.Google Scholar
4. Colliss, S., Babinsky, H., Bruce, P. J. K., Nuler, K. & Lutz, T. 2012 An experimental investigation of three-dimensional shock control bumps applied to transonic airfoils. In 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN. 9th–12th January. AIAA Paper 2012-43.Google Scholar
5. Doerffer, P. & Szwaba, R. 2009 UFAST Experimental Data Bank – Unsteady Effects of Shock Wave Induced Separation (ed. Doerffer, P. ), pp. 131–177. Gdansk.Google Scholar
6. Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8 (12), 1406–1416.CrossRefGoogle Scholar
7. Ogawa, H. & Babinsky, H. 2006 Wind-tunnel setup for investigations of normal shock wave/boundary-layer interaction control. AIAA J. 44 (11), 2803–2805.Google Scholar
8. Sun, C. & Childs, M. 1973 A modified wall wake velocity profile for turbulent compressible boundary layer. J. Aircraft 10 (6), 381–383.CrossRefGoogle Scholar
9. Szwaba, R., Flaszynski, P., Szumski, J. & Telega, J. 2007 Shock wave boundary layer interaction control by air-jet streamwise. In Proceedings of the 8th International Symposium on Experimental and Computational Aerothermodynamics of Internal Flows, Lyon, July.Google Scholar