Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-25T17:41:52.862Z Has data issue: false hasContentIssue false
  • English
  • Français

Control of roughness-induced transition in supersonic flows by local wall heating strips

Published online by Cambridge University Press:  12 November 2024

Zaijie Liu Open the ORCID record for Zaijie Liu [Opens in a new window] ,
Hexia Huang Open the ORCID record for Hexia Huang [Opens in a new window] ,
Huijun Tan  and
Mengying Liu
Zaijie Liu
Affiliation:
College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, PR China
Hexia Huang*
Affiliation:
College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, PR China
Huijun Tan
Affiliation:
College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, PR China
Mengying Liu
Affiliation:
College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

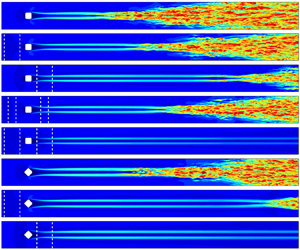
Isolated-roughness-induced transitions controlled by local wall heating strips are studied via direct numerical simulation and BiGlobal linear stability analysis. The transition mechanisms are studied first with different wall temperatures. The separated shear layer–counter-rotating vortex system is found to be the main source for transitions. Symmetric and antisymmetric modes are observed in the wake, and the former is dominant. The local wall heating strip can delay the transition, and this effect is enhanced with higher heating temperature, wider strip and a combination of upstream and downstream control strips. The upstream strip lifts up the inlet flow and weakens the wake system in an indirect manner. The antisymmetric mode gradually vanishes, while the symmetric mode always exists but becomes weaker. The downstream strip exhibits a more effective transition delay by directly weakening the separated shear layer and vortex system in the wake. Vorticity transport analysis suggests that the downstream strip increases dissipation for streamwise vorticity and transfers it into wall-normal and spanwise vorticity. BiGlobal analyses indicate that the downstream strip shows less influence on the peak growth rate of the symmetric mode but significantly shrinks its unstable region. Analyses of the disturbance energy production indicate that the upstream strip wakens the wall-normal and spanwise shear at the same time, but the downstream strip mainly wakens the wall-normal one. More simulations are performed with different roughness heights, point-source disturbance and different roughness shapes. The results show that the current method remains effective enough in delaying transitions at a wide range of conditions.

JFM classification

Instability: Transition to turbulence Compressible Flows: Supersonic flow Flow Control: Instability control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 999 , 25 November 2024 , A16
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Balakumar, P. & Kegerise, M. 2016 Roughness-induced transition in a supersonic boundary layer. AIAA J. 54 (8), 2322–2337.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2012 Compressibility effects on roughness-induced boundary layer transition. Intl J. Heat Mass Transfer 35, 45–51.Google Scholar
Bernardini, M., Pirozzoli, S., Orlandi, P. & Lele, S.K. 2014 Parameterization of boundary-layer transition induced by isolated roughness elements. AIAA J. 52 (10), 2261–2269.CrossRefGoogle Scholar
Chang, C.-L. 2004 Langley stability and transition analysis code (LASTRAC) version 1.2 user manual. NASA Tech. Rep. TM-2004-213233.Google Scholar
De Tullio, N., Paredes, P., Sandham, N.D. & Theofilis, V. 2013 Laminar–turbulent transition induced by a discrete roughness element in a supersonic boundary layer. J. Fluid Mech. 713, 613–646.CrossRefGoogle Scholar
Duan, Z. & Xiao, Z. 2017 Hypersonic transition induced by three isolated roughness elements on a flat plate. Comput. Fluids 157, 1–13.CrossRefGoogle Scholar
Fu, S. & Wang, L. 2013 RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory. Prog. Aerosp. Sci. 58, 36–59.CrossRefGoogle Scholar
Groskopf, G. & Kloker, M.J. 2016 Instability and transition mechanisms induced by skewed roughness elements in a high-speed laminar boundary layer. J. Fluid Mech. 805, 262–302.CrossRefGoogle Scholar
Hamed, A.M., Sadowski, M., Zhang, Z. & Chamorro, L.P. 2016 Transition to turbulence over 2D and 3D periodic large-scale roughnesses. J. Fluid Mech. 804, R6.CrossRefGoogle Scholar
Jiang, G.-S. & Shu, C.-W. 1996 Efficient implementation of weighted eno schemes. J. Comput. Phys. 126 (1), 202–228.CrossRefGoogle Scholar
Kneer, S., Guo, Z. & Kloker, M.J. 2021 Control of laminar breakdown in a supersonic boundary layer employing streaks. J. Fluid Mech. 932, A53.CrossRefGoogle Scholar
Kobayashi, R., Fukunishi, Y., Nishikawa, T. & Kato, T. 1995 The receptivity of flat-plate boundary-layers with two-dimensional roughness elements to freestream sound and its control. In Laminar-Turbulent Transition, pp. 507–514. Springer.CrossRefGoogle Scholar
Kuester, M.S., Sharma, A., White, E.B., Goldstein, D.B. & Brown, G. 2014 Distributed roughness shielding in a blasius boundary layer. AIAA Paper 2014-2888.CrossRefGoogle Scholar
Kuester, M.S. & White, E.B. 2015 Roughness receptivity and shielding in a flat plate boundary layer. J. Fluid Mech. 777, 430–460.CrossRefGoogle Scholar
Li, X., Fu, D. & Ma, Y. 2010 Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack. Phys. Fluids 22 (2), 025105.CrossRefGoogle Scholar
Li, X.-L., Fu, D.-X., Ma, Y.-W. & Gao, H. 2009 Acoustic calculation for supersonic turbulent boundary layer flow. Chin. Phys. Lett. 26 (9), 094701.Google Scholar
Lu, Y., Liu, H., Liu, Z. & Yan, C. 2020 a Assessment and parameterization of upstream shielding effect in quasi-roughness induced transition with direct numerical simulations. Aerosp. Sci. Technol. 100, 105824.CrossRefGoogle Scholar
Lu, Y., Liu, H., Liu, Z. & Yan, C. 2020 b Investigation and parameterization of transition shielding in roughness-disturbed boundary layer with direct numerical simulations. Phys. Fluids 32 (7), 074110.CrossRefGoogle Scholar
Lu, Y., Liu, Z., Sun, M., Zhou, T. & Yan, C. 2022 a Control of roughness-induced transition under the influence of inflow disturbance. Acta Astronaut. 193, 110.CrossRefGoogle Scholar
Lu, Y., Liu, Z., Zhou, T. & Yan, C. 2022 b Stability analysis of roughness-disturbed boundary layer controlled by wall-blowing. Phys. Fluids 34 (10), 104114.CrossRefGoogle Scholar
Lu, Y., Zeng, F., Liu, H., Liu, Z. & Yan, C. 2021 Direct numerical simulation of roughness-induced transition controlled by two-dimensional wall blowing. J. Fluid Mech. 920, A28.CrossRefGoogle Scholar
Mack, L.M. 1984 Boundary-layer linear stability theory. AGARD Report No. 709.Google Scholar
Martín, M.P., Taylor, E.M., Wu, M. & Weirs, V.G. 2006 A bandwidth-optimized weno scheme for the effective direct numerical simulation of compressible turbulence. J. Comput. Phys. 220 (1), 270–289.CrossRefGoogle Scholar
Muppidi, S. & Mahesh, K. 2012 Direct numerical simulations of roughness-induced transition in supersonic boundary layers. J. Fluid Mech. 693, 28–56.CrossRefGoogle Scholar
Pirozzoli, S., Grasso, F. & Gatski, T.B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at $M=2.25$. Phys. Fluids 16 (3), 530–545.CrossRefGoogle Scholar
Redford, J.A., Sandham, N.D. & Roberts, G.T. 2010 Compressibility effects on boundary-layer transition induced by an isolated roughness element. AIAA J. 48 (12), 2818–2830.CrossRefGoogle Scholar
Schneider, S.P. 2008 Effects of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45 (2), 193–209.CrossRefGoogle Scholar
Sharma, A., Drews, S., Kuester, M.S., Goldstein, D.B. & White, E.B. 2014 Evolution of disturbances due to distributed surface roughness in laminar boundary layers. AIAA Paper 2014-0235.CrossRefGoogle Scholar
Sharma, S., Shadloo, M.S., Hadjadj, A. & Kloker, M.J. 2019 Control of oblique-type breakdown in a supersonic boundary layer employing streaks. J. Fluid Mech. 873, 1072–1089.CrossRefGoogle Scholar
Shrestha, P. & Candler, G.V. 2019 Direct numerical simulation of high-speed transition due to roughness elements. J. Fluid Mech. 868, 762–788.CrossRefGoogle Scholar
Steger, J.L. & Warming, R.F. 1981 Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods. J. Comput. Phys. 40 (2), 263–293.CrossRefGoogle Scholar
Subbareddy, P.K., Bartkowicz, M.D. & Candler, G.V. 2014 Direct numerical simulation of high-speed transition due to an isolated roughness element. J. Fluid Mech. 748, 848–878.CrossRefGoogle Scholar
Suryanarayanan, S., Goldstein, D.B., Berger, A.R., White, E.B. & Brown, G.L. 2020 Mechanisms of roughness-induced boundary-layer transition control by shielding. AIAA J. 58 (7), 2951–2963.CrossRefGoogle Scholar
Suryanarayanan, S., Goldstein, D.B., Brown, G.L., Berger, A.R. & White, E.B. 2017 On the mechanics and control of boundary layer transition induced by discrete roughness elements. AIAA Paper 2017-0307.CrossRefGoogle Scholar
White, F.M. 2006 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Zhao, R., Wen, C.Y., Tian, X.D., Long, T.H. & Yuan, W. 2018 Numerical simulation of local wall heating and cooling effect on the stability of a hypersonic boundary layer. Intl J. Heat Mass Transfer 121, 986.CrossRefGoogle Scholar
Zhao, R., Wen, C., Zhou, Y., Tu, G. & Lei, J. 2022 Review of acoustic metasurfaces for hypersonic boundary layer stabilization. Prog. Aerosp. Sci. 130, 100808.CrossRefGoogle Scholar
Zhu, J. 2005 Structured eigenvalue problems and quadratic eigenvalue problems. PhD thesis, University of California, Berkeley.Google Scholar