Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T12:46:59.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Contribution of large-scale motions to the skin friction in a moderate adverse pressure gradient turbulent boundary layer

Published online by Cambridge University Press:  01 June 2018

Min Yoon ,
Jinyul Hwang  and
Hyung Jin Sung Open the ORCID record for Hyung Jin Sung [Opens in a new window]
Min Yoon
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea
Jinyul Hwang
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea
Hyung Jin Sung*
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation of a turbulent boundary layer (TBL) subjected to a moderate adverse pressure gradient (APG, 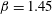$\unicode[STIX]{x1D6FD}=1.45$) is performed to explore the contribution of large scales to the skin friction, where 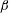$\unicode[STIX]{x1D6FD}$ is the Clauser pressure gradient parameter. The Reynolds number based on the momentum thickness develops from 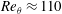$Re_{\unicode[STIX]{x1D703}}\approx 110$ to 6000 with an equilibrium region in 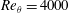$Re_{\unicode[STIX]{x1D703}}=4000$–5500. The spanwise wavelength (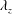$\unicode[STIX]{x1D706}_{z}$) spectra of the streamwise and spanwise velocity fluctuations show that the large-scale energy is significantly enhanced throughout the boundary layer. We quantify the superposition and amplitude modulation effects of these enhanced large scales on the skin friction coefficient (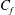$C_{f}$) by employing two approaches: (i) spanwise co-spectra of 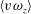$\langle v\unicode[STIX]{x1D714}_{z}\rangle$ and 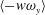$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$; (ii) conditionally averaged 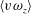$\langle v\unicode[STIX]{x1D714}_{z}\rangle$ and 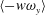$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$. The velocity–vorticity correlations 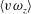$\langle v\unicode[STIX]{x1D714}_{z}\rangle$ and 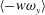$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$ are related to the advective transport and the vortex stretching, respectively. Although 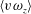$\langle v\unicode[STIX]{x1D714}_{z}\rangle$ negatively contributes to 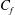$C_{f}$, the positive contribution of the large scales (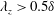$\unicode[STIX]{x1D706}_{z}>0.5\unicode[STIX]{x1D6FF}$) is observed in the co-spectra of weighted 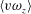$\langle v\unicode[STIX]{x1D714}_{z}\rangle$. For the co-spectra of weighted 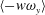$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$, we observe an outer peak at 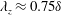$\unicode[STIX]{x1D706}_{z}\approx 0.75\unicode[STIX]{x1D6FF}$ and the superposition of the large scales in the buffer region, leading to the enhancement of 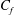$C_{f}$. The magnitude of 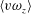$\langle v\unicode[STIX]{x1D714}_{z}\rangle$ and 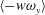$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$ depends on the large-scale streamwise velocity fluctuations (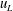$u_{L}$). In particular, the negative-$u_{L}$ events amplify 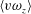$\langle v\unicode[STIX]{x1D714}_{z}\rangle$ in the outer region, and 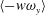$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$ is enhanced by the positive-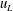$u_{L}$ events. As a result, the skin friction induced by 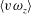$\langle v\unicode[STIX]{x1D714}_{z}\rangle$ and 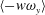$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$ increases in the present APG TBL.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 288 - 311
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. Trans. ASME J. Fluids Engng 126 (5), 835–843.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Ahn, J., Lee, J. H., Jang, S. J. & Sung, H. J. 2013 Direct numerical simulations of fully developed turbulent pipe flows for Re 𝜏 = 180, 544 and 934. Intl J. Heat Fluid Flow 44, 222–228.CrossRefGoogle Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google ScholarPubMed
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23 (6), 061701.Google Scholar
Bobke, A., Vinuesa, R., Örlü, R. & Schlatter, P. 2017 History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 820, 667–692.Google Scholar
Chin, C., Philip, J., Klewicki, J., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aero. Sci. 21 (2), 91–108.Google Scholar
Deck, S., Renard, N., Laraufie, R. & Weiss, P. É. 2014 Large-scale contribution to mean wall shear stress in high-Reynolds-number flat-plate boundary layers up to Re 𝜃 = 13650. J. Fluid Mech. 743, 202–248.Google Scholar
Eyink, G. L. 2008 Turbulent flow in pipes and channels as cross-stream ‘inverse cascades’ of vorticity. Phys. Fluids 20 (12), 125101.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Gungor, A. G., Maciel, Y., Simens, M. P. & Soria, J. 2016 Scaling and statistics of large-defect adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 59, 109–124.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.Google Scholar
Henkes, R. A. W. M. 1998 Scaling of equilibrium boundary layers under adverse pressure gradient using turbulence models. AIAA J. 36 (3), 320–326.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google Scholar
Hwang, J., Lee, J. & Sung, H. J. 2016a Influence of large-scale accelerating motions on turbulent pipe and channel flows. J. Fluid Mech. 804, 420–441.Google Scholar
Hwang, J., Lee, J., Sung, H. J. & Zaki, T. A. 2016b Inner-outer interactions of large-scale structures in turbulent channel flow. J. Fluid Mech. 790, 128–157.Google Scholar
Hwang, J. & Sung, H. J. 2017 Influence of large-scale motions on the frictional drag in a turbulent boundary layer. J. Fluid Mech. 829, 751–779.CrossRefGoogle Scholar
Jacobs, R. G. & Durbin, P. A. 2001 Simulations of bypass transition. J. Fluid Mech. 428, 185–212.CrossRefGoogle Scholar
Kim, J. 2011 Physics and control of wall turbulence for drag reduction. Phil. Trans. R. Soc. Lond A 369 (1940), 1396–1411.Google ScholarPubMed
Kim, J. & Lim, J. 2000 A linear process in wall-bounded turbulent shear flows. Phys. Fluids 12 (8), 1885–1888.Google Scholar
Kim, K., Baek, S. J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kitsios, V., Atkinson, C., Sillero, J. A., Borrell, G., Gungor, A. G., Jiménez, J. & Soria, J. 2016 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer. Intl J. Heat Fluid Flow 61, 129–136.Google Scholar
Kitsios, V., Sekimoto, A., Atkinson, C., Sillero, J. A., Borrell, G., Gungor, A. G., Jiménez, J. & Soria, J. 2017 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer at the verge of separation. J. Fluid Mech. 829, 392–419.Google Scholar
Klewicki, J. C., Murray, J. A. & Falco, R. E. 1994 Vortical motion contributions to stress transport in turbulent boundary layers. Phys. Fluids 6 (1), 277–286.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.Google Scholar
Kravchenko, A. G., Choi, H. & Moin, P. 1993 On the relation of near-wall streamwise vortices to wall skin friction in turbulent boundary layers. Phys. Fluids 5 (12), 3307–3309.Google Scholar
Lee, J., Lee, J. H., Lee, J. H. & Sung, H. J. 2010 Coherent structures in turbulent boundary layers with adverse pressure gradients. J. Turbul. 11 (28), 1–20.Google Scholar
Lee, J. H. 2017 Large-scale motions in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 810, 323–361.Google Scholar
Lee, J. H. & Sung, H. J. 2008 Effects of an adverse pressure gradient on a turbulent boundary layer. Intl J. Heat Fluid Flow 29 (3), 568–578.Google Scholar
Lee, J. H. & Sung, H. J. 2009 Structures in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 639, 101–131.Google Scholar
Maciel, Y., Simens, M. P. & Gungor, A. G. 2017 Coherent structures in a non-equilibrium large-velocity-defect turbulent boundary layer. Flow Turbul. Combust. 98 (1), 1–20.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.Google Scholar
Mellor, G. L. & Gibson, D. M. 1966 Equilibrium turbulent boundary layers. J. Fluid Mech. 24 (02), 225–253.CrossRefGoogle Scholar
Monty, J. P., Harun, Z. & Marusic, I. 2011 A parametric study of adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 32 (3), 575–585.Google Scholar
Örlü, R. & Schlatter, P. 2011 On the fluctuating wall-shear stress in zero pressure-gradient turbulent boundary layer flows. Phys. Fluids 23 (2), 021704.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schlatter, P., Örlü, R., Li, Q., Brethouwer, G., Fransson, J. H., Johansson, A. V., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to Re 𝜃 = 2500 studied through simulation and experiment. Phys. Fluids 21 (5), 051702.Google Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.Google Scholar
Skåre, P. E. & Krogstad, P. Å. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.Google Scholar
Skote, M., Henningson, D. S. & Henkes, R. A. 1998 Direct numerical simulation of self-similar turbulent boundary layers in adverse pressure gradients. Flow Turbul. Combust. 60 (1), 47–85.Google Scholar
Spalart, P. R. & Watmuff, J. H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337–371.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (1), 97–120.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Yoon, M., Ahn, J., Hwang, J. & Sung, H. J. 2016a Contribution of velocity–vorticity correlations to the frictional drag in wall-bounded turbulent flows. Phys. Fluids 28 (8), 081702.CrossRefGoogle Scholar
Yoon, M., Hwang, J., Lee, J., Sung, H. J. & Kim, J. 2016b Large-scale motions in a turbulent channel flow with the slip boundary condition. Intl J. Heat Fluid Flow 61, 96–107.Google Scholar