Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T04:29:12.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Confined flow of suspensions modelled by a frictional rheology

Published online by Cambridge University Press:  22 October 2014

Brice Lecampion  and
Dmitry I. Garagash
Brice Lecampion
Affiliation:
Schlumberger, 1 cours du Triangle, 92936 Paris La Defense, France
Dmitry I. Garagash*
Affiliation:
Department of Civil and Resource Engineering, Dalhousie University, Halifax, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate in detail the problem of confined pressure-driven laminar flow of neutrally buoyant non-Brownian suspensions using a frictional rheology based on the recent proposal of Boyer et al. (Phys. Rev. Lett., vol. 107 (18), 2011, 188301). The friction coefficient (shear stress over particle normal stress) and solid volume fraction are taken as functions of the dimensionless viscous number 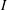$I$ defined as the ratio between the fluid shear stress and the particle normal stress. We clarify the contributions of the contact and hydrodynamic interactions on the evolution of the friction coefficient between the dilute and dense regimes reducing the phenomenological constitutive description to three physical parameters. We also propose an extension of this constitutive framework from the flowing regime (bounded by the maximum flowing solid volume fraction) to the fully jammed state (the random close packing limit). We obtain an analytical solution of the fully developed flow in channel and pipe for the frictional suspension rheology. The result can be transposed to dry granular flow upon appropriate redefinition of the dimensionless number 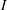$I$. The predictions are in excellent agreement with available experimental results for neutrally buoyant suspensions, when using the values of the constitutive parameters obtained independently from stress-controlled rheological measurements. In particular, the frictional rheology correctly predicts the transition from Poiseuille to plug flow and the associated particles migration with the increase of the entrance solid volume fraction. We also numerically solve for the axial development of the flow from the inlet of the channel/pipe toward the fully developed state. The available experimental data are in good agreement with our numerical predictions, when using an accepted phenomenological description of the relative phase slip obtained independently from batch-settlement experiments. The solution of the axial development of the flow notably provides a quantitative estimation of the entrance length effect in a pipe for suspensions when the continuum assumption is valid. Practically, the latter requires that the predicted width of the central (jammed) plug is wider than one particle diameter. A simple analytical expression for development length, inversely proportional to the gap-averaged diffusivity of a frictional suspension, is shown to encapsulate the numerical solution in the entire range of flow conditions from dilute to dense.

JFM classification

Complex Fluids: Complex Fluids Granular media: Granular media Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 197 - 235
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bacri, J.-C., Frenois, C., Hoyos, M., Perzynski, R., Rakotomalala, N. & Salin, D. 1986 Acoustic study of suspension sedimentation. Europhys. Lett. 2 (2), 123–128.CrossRefGoogle Scholar
Batchelor, G. & Green, J. 1972 The determination of the bulk stress in a suspension of spherical particles to order $c^{2}$ . J. Fluid Mech. 56 (3), 401–427.CrossRefGoogle Scholar
Bear, J. 1972 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Berryman, J. G. 1983 Random close packing of hard spheres and disks. Phys. Rev. A 27 (2), 1053–1061.CrossRefGoogle Scholar
Boyer, F., Guazzelli, É. & Pouliquen, O. 2011a Unifying suspension and granular rheology. Phys. Rev. Lett. 107 (18), 188301.CrossRefGoogle ScholarPubMed
Boyer, F., Pouliquen, O. & Guazzelli, É. 2011b Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.CrossRefGoogle Scholar
Carman, P. 1937 Fluid flow through granular beds. Trans. Inst. Chem. Engrs 15, 150–166.Google Scholar
Cassar, C., Nicolas, M. & Pouliquen, O. 2005 Submarine granular flows down inclined planes. Phys. Fluids 17, 103301.CrossRefGoogle Scholar
Couturier, E., Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 Suspensions in a tilted trough: second normal stress difference. J. Fluid Mech. 686, 26–39.CrossRefGoogle Scholar
Cox, R. & Mason, S. 1971 Suspended particles in fluid flow through tubes. Annu. Rev. Fluid Mech. 3, 291–316.CrossRefGoogle Scholar
Craig, K., Buckholz, R. H. & Domoto, G. 1986 An experimental study of the rapid flow of dry cohesionless metal powders. J. Appl. Mech. 53, 935–942.CrossRefGoogle Scholar
da Cruz, F., Emam, S., Prochnow, M., Roux, J. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys. Rev. E 72, 021309.CrossRefGoogle ScholarPubMed
Davis, R. H. & Acrivos, A. 1985 Sedimentation of noncolloidal particles at low Reynolds numbers. Annu. Rev. Fluid Mech. 17 (1), 91–118.CrossRefGoogle Scholar
Dbouk, T., Lemaire, E., Lobry, L. & Moukalled, F. 2013a Shear-induced particle migration: predictions from experimental evaluation of the particle stress tensor. J. Non-Newtonian Fluid Mech. 198, 78–95.CrossRefGoogle Scholar
Dbouk, T., Lobry, L. & Lemaire, E. 2013b Normal stresses in concentrated non-Brownian suspensions. J. Fluid Mech. 715, 239–272.CrossRefGoogle Scholar
De Gennes, P. 1979 Conjectures on the transition from Poiseuille to plug flow in suspensions. J. Phys. (Paris) 40 (8), 783–787.CrossRefGoogle Scholar
Deboeuf, A., Gauthier, G., Martin, J., Yurkovetsky, Y. & Morris, J. 2009 Particle pressure in a sheared suspension: a bridge from osmosis to granular dilatancy. Phys. Rev. Lett. 102 (10), 108301.CrossRefGoogle Scholar
Einstein, A. 1906 A new determination of molecular dimensions. Ann. Phys. 4 (19), 289–306.CrossRefGoogle Scholar
Fang, Z., Mammoli, A., Brady, J., Ingber, M., Mondy, L. & Graham, A. 2002 Flow-aligned tensor models for suspension flows. Intl J. Multiphase Flow 28 (1), 137–166.CrossRefGoogle Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24.CrossRefGoogle Scholar
Frigaard, I. & Ryan, D. 2004 Flow of a visco-plastic fluid in a channel of slowly varying width. J. Non-Newtonian Fluid Mech. 123 (1), 67–83.CrossRefGoogle Scholar
Garland, S., Gauthier, G., Martin, J. & Morris, J. 2013 Normal stress measurements in sheared non-Brownian suspensions. J. Rheol. 57, 71–88.CrossRefGoogle Scholar
Garside, J. & Al-Dibouni, M. R. 1977 Velocity-voidage relationships for fluidization and sedimentation in solid–liquid systems. Ind. Eng. Chem. Process Des. Dev. 16 (2), 206–214.CrossRefGoogle Scholar
Hampton, R., Mammoli, A., Graham, A., Tetlow, N. & Altobelli, S. 1997 Migration of particles undergoing pressure-driven flow in a circular conduit. J. Rheol. 41, 621–640.CrossRefGoogle Scholar
Isa, L., Besseling, R., Schofield, A. & Poon, W. 2010 Quantitative imaging of concentrated suspensions under flow. High Solid Dispers. 236, 163–202.CrossRefGoogle Scholar
Jackson, R. 2000 The Dynamics of Fluidized Particles. Cambridge University Press.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.CrossRefGoogle ScholarPubMed
Karnis, A., Goldsmith, H. & Mason, S. 1966 The kinetics of flowing dispersions: I. Concentrated suspensions of rigid particles. J. Colloid Interface Sci. 22 (6), 531–553.CrossRefGoogle Scholar
Knight, J. B., Fandrich, C. G., Lau, C. N., Jaeger, H. M. & Nagel, S. R. 1995 Density relaxation in a vibrated granular material. Phys. Rev. E 51 (5), 3957–3963.CrossRefGoogle Scholar
Kozeny, J. 1927 Ueber kapillare leitung des wassers im boden. Sitz.ber. Akad. Wiss. Wien 136, 271–306.Google Scholar
Krieger, I. & Dougherty, T. 1959 A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 3, 137–152.CrossRefGoogle Scholar
Ladd, A. C. 1990 Hydrodynamic transport coefficients of random dispersions of hard spheres. J. Chem. Phys. 93 (5), 3484–3494.CrossRefGoogle Scholar
Leighton, D. & Acrivos, A. 1987 The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181 (1), 415–439.CrossRefGoogle Scholar
Lyon, M. & Leal, L. 1998a An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 1. Monodisperse systems. J. Fluid Mech. 363, 25–56.CrossRefGoogle Scholar
Lyon, M. & Leal, L. 1998b An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 2. Bidisperse systems. J. Fluid Mech. 363, 57–77.CrossRefGoogle Scholar
MiDi, G. 2004 On dense granular flows. Eur. Phys. J. E 14, 341–365.CrossRefGoogle Scholar
Miller, R. & Morris, J. 2006 Normal stress-driven migration and axial development in pressure-driven flow of concentrated suspensions. J. Non-Newtonian Fluid Mech. 135 (2), 149–165.CrossRefGoogle Scholar
Mills, P. & Snabre, P. 1994 Settling of a suspension of hard spheres. Europhys. Lett. 25 (9), 651–656.CrossRefGoogle Scholar
Mills, P. & Snabre, P. 1995 Rheology and structure of concentrated suspensions of hard spheres. Shear induced particle migration. J. Phys. II 5 (10), 1597–1608.Google Scholar
Morris, J. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 43, 1213–1237.CrossRefGoogle Scholar
Muir Wood, D. 1990 Soil Behaviour and Critical State Soil Mechanics. Cambridge University Press.Google Scholar
Nott, P. & Brady, J. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157–200.CrossRefGoogle Scholar
Ovarlez, G., Bertrand, F. & Rodts, S. 2006 Local determination of the constitutive law of a dense suspension of noncolloidal particles through magnetic resonance imaging. J. Rheol. 50, 259–292.CrossRefGoogle Scholar
Pailha, M. & Pouliquen, O. 2009 A two-phase flow description of the initiation of underwater granular avalanches. J. Fluid Mech. 633, 115–135.CrossRefGoogle Scholar
Peyneau, P. & Roux, J. 2008 Frictionless bead packs have macroscopic friction, but no dilatancy. Phys. Rev. E 78, 011307.CrossRefGoogle ScholarPubMed
Phillips, R., Armstrong, R. & Brown, R. 1992 Constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids 4 (1), 30–40.CrossRefGoogle Scholar
Pouliquen, O., Belzons, M. & Nicolas, M. 2003 Fluctuating particle motion during shear induced granular compaction. Phys. Rev. Lett. 91 (1), 014301.CrossRefGoogle ScholarPubMed
Ramachandran, A. 2013 A macrotransport equation for the particle distribution in the flow of a concentrated, non-colloidal suspension through a circular tube. J. Fluid Mech. 734, 219–252.CrossRefGoogle Scholar
Ramachandran, A. & Leighton, D. T. 2008 The influence of secondary flows induced by normal stress differences on the shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 603, 207–243.CrossRefGoogle Scholar
Richardson, J. & Zaki, W. 1954 Sedimentation and fluidization: Part I. Trans. Inst. Chem. Engrs 32, 35–47.Google Scholar
Rognon, R. G., Roux, J., Naaim, M. & Chevoir, F. 2008 Dense flows of cohesive granular materials. J. Fluid Mech. 596, 21–47.CrossRefGoogle Scholar
Scott, G. & Kilgour, D. 1969 The density of random close packing of spheres. J. Phys. D: Appl. Phys. 2 (6), 863–866.CrossRefGoogle Scholar
Seshadri, V. & Sutera, S. P. 1968 Concentration changes of suspensions of rigid spheres flowing through tubes. J. Colloid Interface Sci. 27 (1), 101–110.CrossRefGoogle Scholar
Sinton, S. W. & Chow, A. W. 1991 NMR flow imaging of fluids and solid suspensions in Poiseuille flow. J. Rheol. 35, 735–772.CrossRefGoogle Scholar
Stickel, J. & Powell, R. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.CrossRefGoogle Scholar
von Terzaghi, K. 1940 Theoretical Soil Mechanics. Wiley.Google Scholar
Zarraga, I., Hill, D. & Leighton, D. Jr 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44, 185–220.CrossRefGoogle Scholar
Supplementary material: PDF

Lecampion and Garagash supplementary material

Figures S1-S4

Download Lecampion and Garagash supplementary material(PDF)
PDF 1.2 MB