Article contents
Conditioning of cross-flow instability modes using dielectric barrier discharge plasma actuators
Published online by Cambridge University Press: 02 November 2017
Abstract
In the current study, selective forcing of cross-flow instability modes evolving on a 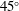 $45^{\circ }$ swept wing at
$45^{\circ }$ swept wing at 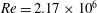 $Re=2.17\times 10^{6}$ is achieved by means of spanwise-modulated plasma actuators, positioned near the leading edge. In the perspective of laminar flow control, the followed methodology holds on the discrete roughness elements/upstream flow deformation (DRE/UFD) approach, thoroughly investigated by e.g. Saric et al. (AIAA Paper 1998-781, 1998), Malik et al. (J. Fluid Mech., vol. 399, 1999, pp. 85–115) and Wassermann & Kloker (J. Fluid Mech., vol. 456, 2002, pp. 49–84). The possibility of using active devices for UFD provides several advantages over passive means, allowing for a wider range of operating
$Re=2.17\times 10^{6}$ is achieved by means of spanwise-modulated plasma actuators, positioned near the leading edge. In the perspective of laminar flow control, the followed methodology holds on the discrete roughness elements/upstream flow deformation (DRE/UFD) approach, thoroughly investigated by e.g. Saric et al. (AIAA Paper 1998-781, 1998), Malik et al. (J. Fluid Mech., vol. 399, 1999, pp. 85–115) and Wassermann & Kloker (J. Fluid Mech., vol. 456, 2002, pp. 49–84). The possibility of using active devices for UFD provides several advantages over passive means, allowing for a wider range of operating 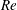 $Re$ numbers and pressure distributions. In the present work, customised alternating current dielectric barrier discharge plasma actuators have been designed, manufactured and characterised. The authority of the actuators in forcing monochromatic stationary cross-flow modes at different spanwise wavelengths is assessed by means of infrared thermography. Moreover, quantitative spatio-temporal measurements of the boundary layer velocity field are performed using time-resolved particle image velocimetry. The results reveal distinct steady and unsteady forcing contributions of the plasma actuator on the boundary layer. It is shown that the actuators introduce unsteady fluctuations in the boundary layer, amplifying at frequencies significantly lower than the actuation frequency. In line with the DRE/UFD strategy, forcing a sub-critical stationary mode, with a shorter wavelength compared to the naturally selected mode, results in less amplified primary vortices and related fluctuations, compared to the critical forcing case. The effect of the forcing on the flow stability is further inspected by combining the measured actuators body force with the numerical solution of the laminar boundary layer and linear stability theory. The simplified methodology yields fast and computationally cheap estimates on the effect of steady forcing (magnitude and direction) on the boundary layer stability.
$Re$ numbers and pressure distributions. In the present work, customised alternating current dielectric barrier discharge plasma actuators have been designed, manufactured and characterised. The authority of the actuators in forcing monochromatic stationary cross-flow modes at different spanwise wavelengths is assessed by means of infrared thermography. Moreover, quantitative spatio-temporal measurements of the boundary layer velocity field are performed using time-resolved particle image velocimetry. The results reveal distinct steady and unsteady forcing contributions of the plasma actuator on the boundary layer. It is shown that the actuators introduce unsteady fluctuations in the boundary layer, amplifying at frequencies significantly lower than the actuation frequency. In line with the DRE/UFD strategy, forcing a sub-critical stationary mode, with a shorter wavelength compared to the naturally selected mode, results in less amplified primary vortices and related fluctuations, compared to the critical forcing case. The effect of the forcing on the flow stability is further inspected by combining the measured actuators body force with the numerical solution of the laminar boundary layer and linear stability theory. The simplified methodology yields fast and computationally cheap estimates on the effect of steady forcing (magnitude and direction) on the boundary layer stability.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 44
- Cited by


