Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-09T08:50:39.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Computationally generated constitutive models for particle phase rheology in gas-fluidized suspensions

Published online by Cambridge University Press:  04 December 2018

Yile Gu Open the ORCID record for Yile Gu [Opens in a new window] ,
Ali Ozel ,
Jari Kolehmainen Open the ORCID record for Jari Kolehmainen [Opens in a new window]  and
Sankaran Sundaresan
Yile Gu*
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08540, USA
Ali Ozel
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08540, USA School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh EH14 4AS, UK
Jari Kolehmainen
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08540, USA
Sankaran Sundaresan
Affiliation:
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08540, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Developing constitutive models for particle phase rheology in gas-fluidized suspensions through rigorous statistical mechanical methods is very difficult when complex inter-particle forces are present. In the present study, we pursue a computational approach based on results obtained through Eulerian–Lagrangian simulations of the fluidized state. Simulations were performed in a periodic domain for non-cohesive and mildly cohesive (Geldart Group A) particles. Based on the simulation results, we propose modified closures for pressure, bulk viscosity, shear viscosity and the rate of dissipation of pseudo-thermal energy. 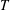For non-cohesive particles, results in the high granular temperature $T$ regime agree well with constitutive expressions afforded by the kinetic theory of granular materials, demonstrating the validity of the methodology. The simulations reveal a low 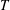$T$ regime, where the inter-particle collision time is determined by gravitational fall between collisions. Inter-particle cohesion has little effect in the high 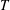$T$ regime, but changes the behaviour appreciably in the low 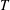$T$ regime. At a given 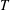$T$, a cohesive particle system manifests a lower pressure at low particle volume fractions when compared to non-cohesive systems; at higher volume fractions, the cohesive assemblies attain higher coordination numbers than the non-cohesive systems, and experience greater pressures. Cohesive systems exhibit yield stress, which is weakened by particle agitation, as characterized by 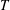$T$. All these effects are captured through simple modifications to the kinetic theory of granular materials for non-cohesive materials.

JFM classification

Rarefied Gas Flow: Kinetic theory Multiphase and Particle-laden Flows: Particle/fluid flow Non-Newtonian Flows: Rheology
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 318 - 349
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aarons, L. & Sundaresan, S. 2006 Shear flow of assemblies of cohesive and non-cohesive granular materials. Powder Technol. 169 (1), 10–21.Google Scholar
Agrawal, K., Loezos, P. N., Syamlal, M. & Sundaresan, S. 2001 The role of meso-scale structures in rapid gas–solid flows. J. Fluid Mech. 445, 151–185.Google Scholar
Alam, M. & Nott, P. R. 1997 The influence of friction on the stability of unbounded granular shear flow. J. Fluid Mech. 343, 267–301.Google Scholar
Arastoopour, H. 2001 Numerical simulation and experimental analysis of gas/solid flow systems: 1999 {Fluor-Daniel} Plenary lecture. Powder Technol. 119 (2–3), 59–67.Google Scholar
Balzer, G., Boëlle, A. & Simonin, O. 1995 Fluidized, Eulerian gas–solid flow modelling of dense fluidized beds. In Fluidization VIII, p. 1125.Google Scholar
Beetstra, R., van der Hoef, M. A. & Kuipers, J. A. M. 2007 Drag force of intermediate reynolds number flow past mono- and bidisperse arrays of spheres. AIChE J. 53 (2), 489–501.Google Scholar
Berzi, D. & Vescovi, D. 2015 Different singularities in the functions of extended kinetic theory at the origin of the yield stress in granular flows. Phys. Fluids 27 (1), 013302.Google Scholar
Boëlle, A., Balzer, G. & Simonin, O. 1995 Second-order prediction of the particle-phase stress tensor of inelastic spheres in simple shear dense suspensions. In Proceedings of the 6th International Symposium on Gas–Solid Flows, ASME FED, vol. 228, pp. 9–18.Google Scholar
Boyce, C. M., Ozel, A., Kolehmainen, J. & Sundaresan, S. 2017 Analysis of the effect of small amounts of liquid on gas–solid fluidization using CFD-DEM simulations. AIChE J. 63 (12), 1547–5905.Google Scholar
Campbell, C. S. 2002 Granular shear flows at the elastic limit. J. Fluid Mech. 465, 261–291.Google Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2014 Numerical study of collisional particle dynamics in cluster-induced turbulence. J. Fluid Mech. 747, R2.Google Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2015 On fluid-particle dynamics in fully developed cluster-induced turbulence. J. Fluid Mech. 780, 578–635.Google Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2016a Strongly coupled fluid-particle flows in vertical channels. I. Reynolds-averaged two-phase turbulence statistics. Phys. Fluids 28 (3), 033306.Google Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2016b Strongly coupled fluid-particle flows in vertical channels. II. Turbulence modeling. Phys. Fluids 28 (3), 033307.Google Scholar
Chialvo, S., Sun, J. & Sundaresan, S. 2012 Bridging the rheology of granular flows in three regimes. Phys. Rev. E 85 (2), 021305.Google Scholar
Chialvo, S. & Sundaresan, S. 2013 A modified kinetic theory for frictional granular flows in dense and dilute regimes. Phys. Fluids 25 (7), 070603.Google Scholar
da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys. Rev. E 72 (2), 21309.Google Scholar
Cundall, P. A. & Strack, O. D. L. 1979 A discrete numerical model for granular assemblies. Geotechnique 29 (1), 47–65.Google Scholar
Derksen, J. J. & Sundaresan, S. 2007 Direct numerical simulations of dense suspensions: wave instabilities in liquid-fluidized beds. J. Fluid Mech. 587, 303–336.Google Scholar
Doi, T., Santos, A. & Tij, M. 1999 Numerical study of the influence of gravity on the heat conductivity on the basis of kinetic theory. Phys. Fluids 11 (11), 3553–3559.Google Scholar
Février, P., Simonin, O. & Squires, K. D. 2005 Partitioning of particle velocities in gas–solid turbulent flows into a continuous field and a spatially uncorrelated random distribution: theoretical formalism and numerical study. J. Fluid Mech. 533, 1–46.Google Scholar
Forsyth, A. J., Hutton, S. & Rhodes, M. J. 2002 Effect of cohesive interparticle force on the flow characteristics of granular material. Powder Technol. 126, 150–154.Google Scholar
Fox, R. O. 2014 On multiphase turbulence models for collisional fluid-particle flows. J. Fluid Mech. 742, 368–424.Google Scholar
Garzó, V. & Dufty, J. W. 1999 Dense fluid transport for inelastic hard spheres. Phys. Rev. E 59 (5), 5895–5911.Google Scholar
Garzó, V., Tenneti, S., Subramaniam, S. & Hrenya, C. M. 2012 Enskog kinetic theory for monodisperse gas–solid flows. J. Fluid Mech. 712, 129–168.Google Scholar
Geldart, D. 1973 Types of gas fluidization. Powder Technol. 7, 285–292.Google Scholar
Gidaspow, D. 1994 Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions. Academic Press.Google Scholar
Gidaspow, D. & Huilin, L. 1998 Equation of state and radial distribution functions of FCC particles in a CFB. AIChE J. 44 (2), 279–293.Google Scholar
Goldstein, D., Handler, R. & Sirovich, L. 1993 Modeling a no-slip flow boundary with an external force field. J. Comput. Phys. 105 (2), 354–366.Google Scholar
Goniva, C., Kloss, C., Deen, N. G., Kuipers, J. A. M. & Pirker, S. 2012 Influence of rolling friction on single spout fluidized bed simulation. Particuology 10 (5), 582–591.Google Scholar
Gu, Y., Chialvo, S. & Sundaresan, S. 2014 Rheology of cohesive granular materials across multiple dense-flow regimes. Phys. Rev. E 90 (3), 32206.Google Scholar
Gu, Y., Ozel, A. & Sundaresan, S. 2016a A modified cohesion model for CFD-DEM simulations of fluidization. Powder Technol. 296, 17–28.Google Scholar
Gu, Y., Ozel, A. & Sundaresan, S. 2016b Numerical studies of the effects of fines on fluidization. AIChE J. 62 (7), 2271–2281.Google Scholar
Gu, Y., Ozel, A. & Sundaresan, S. 2016c Rheology of granular materials with size distributions across dense-flow regimes. Powder Technol. 295, 322–329.Google Scholar
Hamaker, H. C. 1937 The London-van der Waals attraction between spherical particles. Physica 4 (10), 1058–1072.Google Scholar
Hou, Q. F., Zhou, Z. Y. & Yu, A. B. 2012 Micromechanical modeling and analysis of different flow regimes in gas fluidization. Chem. Engng Sci. 84, 449–468.Google Scholar
Irani, E., Chaudhuri, P. & Heussinger, C. 2014 Impact of attractive interactions on the rheology of dense athermal particles. Phys. Rev. Lett. 112 (18).Google Scholar
Israelachvili, J. N. 2010 Intermolecular and Surface Forces, 3rd edn. Academic Press.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985a Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87 (4).Google Scholar
Jenkins, J. T. & Richman, M. W. 1985b Kinetic theory for plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28 (12), 3485–3494.Google Scholar
Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 130, 187–202.Google Scholar
Jenkins, J. T. & Zhang, C. 2002 Kinetic theory for identical, frictional, nearly elastic spheres. Phys. Fluids 14 (3), 1228–1235.Google Scholar
Johnson, K. L. 1987 Contact Mechanics. Cambridge University Press.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441, 727–730.Google Scholar
Kellogg, K. M., Liu, P., LaMarche, C. Q. & Hrenya, C. M. 2017 Continuum theory for rapid cohesive-particle flows: general balance equations and discrete-element-method-based closure of cohesion-specific quantities. J. Fluid Mech. 832, 345–382.Google Scholar
Kim, H. & Arastoopour, H. 2002 Extension of kinetic theory to cohesive particle flow. Powder Technol. 122 (1), 83–94.Google Scholar
Kim, O. V. & Dunn, P. F. 2007 A microsphere-surface impact model for implementation in computational fluid dynamics. J. Aerosol. Sci. 38 (5), 532–549.Google Scholar
Kloss, C., Goniva, C., Hager, A., Amberger, S. & Pirker, S. 2012 Models, algorithms and validation for opensource DEM and CFD–DEM. Prog. Comput. Fluid Dyn. 12 (2), 140–152.Google Scholar
Kobayashi, T., Tanaka, T., Shimada, N. & Kawaguchi, T. 2013 DEM-CFD analysis of fluidization behavior of Geldart Group A particles using a dynamic adhesion force model. Powder Technol. 248, 143–152.Google Scholar
Koch, D. L. 1990 Kinetic theory for a monodisperse gas–solid suspension. Phys. Fluids A 2 (10), 1711.Google Scholar
Koch, D. L. & Sangani, A. S. 1999 Particle pressure and marginal stability limits for a homogeneous monodisperse gas-fluidized bed: kinetic theory and numerical simulations. J. Fluid Mech. 400, 229–263.Google Scholar
Kolehmainen, J., Ozel, A., Boyce, C. M. & Sundaresan, S. 2016 A hybrid approach to computing electrostatic forces in fluidized beds of charged particles. AIChE J. 62 (7), 2282–2295.Google Scholar
Kumaran, V. 2004 Constitutive relations and linear stability of a sheared granular flow. J. Fluid Mech. 506, 1–43.Google Scholar
Kumaran, V. 2006 The constitutive relation for the granular flow of rough particles, and its application to the flow down an inclined plane. J. Fluid Mech. 561, 1–42.Google Scholar
Kuwagi, K., Mikami, T. & Horio, M. 2000 Numerical simulation of metallic solid bridging particles in a fluidized bed at high temperature. Powder Technol. 109 (1–3), 27–40.Google Scholar
Liu, P., LaMarche, C. Q., Kellogg, K. M. & Hrenya, C. M. 2016 Fine-particle defluidization: Interaction between cohesion, Youngs modulus and static bed height. Chem. Engng Sci. 145, 266–278.Google Scholar
Lun, C. K. K. 1991 Kinetic theory for granular flow of dense, slightly inelastic, slightly rough spheres. J. Fluid Mech. 233, 539–559.Google Scholar
Lun, C. K. K. & Savage, S. B. 2003 Kinetic theory for inertia flows of dilute turbulent gas–solids mixtures. In Granular Gas Dynamics (ed. Pöschel, T. & Brilliantov, N.), pp. 267–289. Springer.Google Scholar
Lun, C. K. K., Savage, S. B., Jeffrey, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 140, 223–256.Google Scholar
Ma, X. & Kato, K. 1998 Effect of interparticle adhesion forces on elutriation of fine powders from a fluidized bed of a binary particle mixture. Powder Technol. 95 (2), 93–101.Google Scholar
Marchisio, D. L. & Fox, R. O. 2013 Computational {Models} for {Polydisperse} {Particulate} and {Multiphase} {Systems}. Cambridge University Press.Google Scholar
Marchisio, D. L., Vigil, R. D. & Fox, R. O. 2003 Quadrature method of moments for aggregation–breakage processes. J. Colloid Interface Sci. 258 (2), 322–334.Google Scholar
Maurin, R., Chauchat, J. & Frey, P. 2016 Dense granular flow rheology in turbulent bedload transport. J. Fluid Mech. 804, 490–512.Google Scholar
Menon, N. & Durian, D. J. 1997 Particle motions in a gas-fluidized bed of sand. Phys. Rev. Lett. 79 (18), 3407–3410.Google Scholar
MiDi, G. D. R. 2004 On dense granular flows. Eur. Phys. J. E 14, 341–365.Google Scholar
Moon, S. J., Kevrekidis, G. I. & Sundaresan, S. 2006 Compaction and dilation rate dependence of stresses in gas-fluidized beds. Phys. Fluids 18 (8), 083304.Google Scholar
Moreno-Atanasio, R., Xu, B. H. & Ghadiri, M. 2007 Computer simulation of the effect of contact stiffness and adhesion on the fluidization behaviour of powders. Chem. Engng Sci. 62 (1–2), 184–194.Google Scholar
Murphy, E. & Subramaniam, S. 2015 Freely cooling granular gases with short-ranged attractive potentials. Phys. Fluids 27 (4), 043301.Google Scholar
Murphy, E. & Subramaniam, S. 2017 Binary collision outcomes for inelastic soft-sphere models with cohesion. Powder Technol. 305, 462–476.Google Scholar
Ocone, R., Sundaresan, S. & Jackson, R. 1993 Gas–particle flow in a duct of arbitrary inclination with particle–particle interactions. AIChE J. 39 (8), 1261–1271.Google Scholar
Olsson, P. & Teitel, S. 2007 Critical scaling of shear viscosity at the jamming transition. Phys. Rev. Lett. 99 (17), 178001.Google Scholar
OpenCFD2013 OpenFOAM 2.2.2 User Manual.Google Scholar
Otsuki, M. & Hayakawa, H. 2009 Critical behaviors of sheared frictionless granular materials near the jamming transition. Phys. Rev. E 80, 11308.Google Scholar
Ozel, A., Gu, Y., Milioli, C. C., Kolehmainen, J. & Sundaresan, S. 2017 Towards filtered drag force model for non-cohesive and cohesive particle-gas flows. Phys. Fluids 29 (10), 103308.Google Scholar
Ozel, A., Kolehmainen, J., Radl, S. & Sundaresan, S. 2016 Fluid and particle coarsening of drag force for discrete-parcel approach. Chem. Engng Sci. 155, 258–267.Google Scholar
Picard, G., Ajdari, A., Bocquet, L. & Lequeux, F. 2002 Simple model for heterogeneous flows of yield stress fluids. Phys. Rev. E 66 (5), 051501.Google Scholar
Renzo, A. D. & Maio, F. P. D. 2004 Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Engng Sci. 59 (3), 525–541.Google Scholar
Rognon, P. G., Roux, J.-N., Naaïm, M. & Chevoir, F. 2008 Dense flows of cohesive granular materials. J. Fluid Mech. 596, 21–47.Google Scholar
Rognon, P. G., Roux, J.-N., Naaïm, M. & Chevoir, F. 2007 Dense flows of bidisperse assemblies of disks down an inclined plane. Phys. Fluids 19 (5), 58101.Google Scholar
Saitoh, K., Takada, S. & Hayakawa, H. 2015 Hydrodynamic instabilities in shear flows of dry cohesive granular particles. Soft Matt. 11 (32), 6371–6385.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid flows of smooth inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41–74.Google Scholar
Sela, N., Goldhirsch, I. & Noskowicz, S. H. 1996 Kinetic theoretical study of a simply sheared two-dimensional granular gas to Burnett order. Phys. Fluids 8 (9), 2337–2353.Google Scholar
Seu-Kim, H. & Arastoopour, H. 1995 Simulation of {FCC} particles flow behavior in a {CFB} using modified kinetic theory. Can. J. Chem. Engng 73 (5), 603–611.Google Scholar
Srivastava, A. & Sundaresan, S. 2003 Analysis of a frictional–kinetic model for gas–particle flow. Powder Technol. 129 (1–3), 72–85.Google Scholar
Sun, J. & Sundaresan, S. 2011 A constitutive model with microstructure evolution for flow of rate-independent granular materials. J. Fluid Mech. 682, 590–616.Google Scholar
Takada, S., Saitoh, K. & Hayakawa, H. 2014 Simulation of cohesive fine powders under a plane shear. Phys. Rev. E 90 (6), 062207.Google Scholar
Takada, S., Saitoh, K. & Hayakawa, H. 2016 Kinetic theory for dilute cohesive granular gases with a square well potential. Phys. Rev. E 94 (1), 12906.Google Scholar
Tripathi, A. & Khakhar, D. V. 2011 Rheology of binary granular mixtures in the dense flow regime. Phys. Fluids 23 (11), 113302.Google Scholar
Van Wachem, B. & Sasic, S. 2008 Derivation, simulation and validation of a cohesive particle flow CFD model. AIChE J. 54 (1), 9–19.Google Scholar
Wen, C. Y. & Yu, Y. H. 1966 Mechanics of fluidization. Chem. Engng Prog. 62 (62), 100–111.Google Scholar
Wilson, R., Dini, D. & van Wachem, B. 2016 A numerical study exploring the effect of particle properties on the fluidization of adhesive particles. AIChE J. 62 (5), 1467–1477.Google Scholar
Winitzki, S. 2003 Uniform approximations for transcendental functions. In Computational Science and Its Applications – ICCSA 2003: International Conference Montreal, Canada, May 18–21, 2003 Proceedings, Part I (ed. Kumar, V., Gavrilova, M. L., Kenneth Tan, C. J. & L’Ecuyer, P.), pp. 780–789. Springer.Google Scholar
Yang, L. L., Padding, J. T. J. & Kuipers, J. A. M. H. 2016 Modification of kinetic theory of granular flow for frictional spheres. Part I: two-fluid model derivation and numerical implementation. Chem. Engng Sci. 152, 767–782.Google Scholar
Yang, R., Zou, R. & Yu, A. 2000 Computer simulation of the packing of fine particles. Phys. Rev. E 62 (3 Pt B), 3900–3908.Google Scholar
Ye, M., Van Der Hoef, M. A. & Kuipers, J. A. M. 2005 From discrete particle model to a continuous model of geldart a particles. Chem. Engng Res. Des. 83 (7), 833–843.Google Scholar
Zhou, Z. Y., Kuang, S. B., Chu, K. W. & Yu, A. B. 2010 Discrete particle simulation of particle-fluid flow: model formulations and their applicability. J. Fluid Mech. 661, 482–510.Google Scholar