Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T06:44:40.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison between spatial and temporal wall oscillations in turbulent boundary layer flows

Published online by Cambridge University Press:  30 July 2013

Martin Skote
Martin Skote*
Affiliation:
School of Mechanical & Aerospace Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798, Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations have been performed to study the drag reduction resulting from spatial oscillations of a segment of the wall under a turbulent boundary layer. The oscillating motion is imposed by utilizing a streamwise modulated spanwise wall forcing. The results are compared with earlier simulations using temporal oscillations with an identical segment and forcing amplitudes, and with a frequency related to the wavelength through a convective velocity. Two different oscillation amplitudes with equal oscillation wavelength have been used, which allows for a direct comparison between a relatively weak and strong forcing of the flow. The weaker forcing results in 25 % drag reduction while the stronger forcing, with twice the amplitude, yields 41 % drag reduction. Comparison with the temporal cases reveals drastically improved energy savings for the spatial oscillation technique, in accordance with earlier channel flow investigations. The streamwise variation of spanwise shear is shown to follow the analytical solution to the laminar Navier–Stokes equations derived under the assumption of constant friction velocity. Furthermore, the spanwise velocity profiles at various phases are compared with the analytical solution, and show very good agreement. 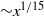The downstream development of the spatial Stokes layer thickness is theoretically estimated to be ${\sim }{x}^{1/ 15} $, in general agreement with the simulation data. The spatial variation of the spanwise Reynolds stress is investigated and compared with the variation in time for the temporal wall forcing cases. The controversy regarding a zero or non-zero production of spanwise Reynolds stress in the temporal case is elucidated. In addition, comparison with the spatial case reveals that a second production term originating from the downstream variation of the spanwise wall velocity has a negative contribution to the production, and hence relates to the larger drag reduction in the case of spatial forcing.

JFM classification

Flow Control: Flow Control Turbulent Flows: Turbulent boundary layers Flow Control: Drag reduction
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 273 - 294
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auteri, F., Baron, A., Belan, M., Campanardi, G. & Quadrio, M. 2010 Experimental assessment of drag reduction by traveling waves in a turbulent pipe flow. Phys. Fluids 22, 115103.CrossRefGoogle Scholar
Baron, A. & Quadrio, M. 1996 Turbulent drag reduction by spanwise wall oscillations. Appl. Sci. Res. 55, 311–326.CrossRefGoogle Scholar
Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S. 2007 SIMSON: a pseudo-spectral solver for incompressible boundary layer flows. Tech. Rep. TRITA-MEK 2007:07, KTH Mechanics, Stockholm, Sweden.Google Scholar
Choi, K.-S. 2002 Near-wall structure of turbulent boundary layer with spanwise-wall oscillation. Phys. Fluids 14, 2530–2542.CrossRefGoogle Scholar
Choi, K. S. & Clayton, B. R. 2001 The mechanism of turbulent drag reduction with wall oscillation. Intl J. Heat Fluid Flow 22 (1), 1–9.CrossRefGoogle Scholar
Choi, K. S & Graham, M 1998 Drag reduction of turbulent pipe flows by circular-wall oscillation. Phys. Fluids 10 (1), 7–9.CrossRefGoogle Scholar
Choi, J.-I., Xu, C. X. & Sung, H. J. 2002 Drag reduction by spanwise wall oscillation in wall-bounded turbulent flows. AIAA J. 40 (5), 842–850.CrossRefGoogle Scholar
Di Cicca, G. M., Iuso, G., Spazzini, P. G. & Onorato, M. 2002 Particle image velocimetry investigation of a turbulent boundary layer manipulated by spanwise wall oscillations. J. Fluid Mech. 467, 41–56.CrossRefGoogle Scholar
Duggleby, A., Ball, K. S. & Paul, M. R. 2007 The effect of spanwise wall oscillation on turbulent pipe flow structures resulting in drag reduction. Phys. Fluids 19, 125107.CrossRefGoogle Scholar
Hasegawa, Y. & Kasagi, N. 2011 Dissimilar control of momentum and heat transfer in a fully developed turbulent channel flow. J. Fluid Mech. 683, 57–93.CrossRefGoogle Scholar
Jung, W. J., Mangiavacchi, N. & Akhavan, R. 1992 Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations. Phys. Fluids A 4 (8), 1605–1607.CrossRefGoogle Scholar
Karniadakis, G. E. & Choi, K. S. 2003 Mechanisms on transverse motions in turbulent wall flows. Annu. Rev. Fluid Mech. 35, 45–62.CrossRefGoogle Scholar
Kasagi, N., Suzuki, Y. & Fukagata, K. 2009 Microelectromechanical systems-based feedback control of turbulence for skin friction reduction. Annu. Rev. Fluid Mech. 41, 231–251.CrossRefGoogle Scholar
Laadhari, F., Skandaji, L. & Morel, R. 1994 Turbulence reduction in a boundary layer by a local spanwise oscillating surface. Phys. Fluids 6, 3218–3220.CrossRefGoogle Scholar
Nikitin, N. V. 2000 On the mechanism of turbulence suppression by spanwise surface oscillations. Fluid Dyn. 35 (2), 185–190.CrossRefGoogle Scholar
Quadrio, M. & Ricco, P. 2003 Initial response of a turbulent channel flow to spanwise oscillation of the walls. J. Turbul. 4 (7), 1–23.CrossRefGoogle Scholar
Quadrio, M. & Ricco, P. 2004 Critical assessment of turbulent drag reduction through spanwise wall oscillations. J. Fluid Mech. 521, 251–271.CrossRefGoogle Scholar
Quadrio, M. & Ricco, P. 2011 The laminar generalized Stokes layer and turbulent drag reduction. J. Fluid Mech. 667, 135–157.CrossRefGoogle Scholar
Quadrio, M., Ricco, P. & Viotti, C. 2009 Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction. J. Fluid Mech. 627, 161–178.CrossRefGoogle Scholar
Quadrio, M. & Sibilla, S. 2000 Numerical simulation of turbulent flow in a pipe oscillating around its axis. J. Fluid Mech. 424, 217–241.CrossRefGoogle Scholar
Ricco, P. 2004 Modification of near-wall turbulence due to spanwise wall oscillations. J. Turbul. 5 (24), 1–18.CrossRefGoogle Scholar
Ricco, P. 2011 Laminar streaks with spanwise wall forcing. Phys. Fluids 23, 064103.CrossRefGoogle Scholar
Ricco, P. & Hahn, S. 2013 Turbulent drag reduction through rotating discs. J. Fluid Mech. 722, 267–290.CrossRefGoogle Scholar
Ricco, P., Ottonelli, C., Hasegawa, Y. & Quadrio, M. 2012 Changes in turbulent dissipation in a channel flow with oscillating walls. J. Fluid Mech. 700, 77–104.CrossRefGoogle Scholar
Ricco, P. & Quadrio, M. 2008 Wall-oscillation conditions for drag reduction in turbulent channel flow. Intl J. Heat Fluid Flow 29 (4), 601–612.CrossRefGoogle Scholar
Ricco, P. & Wu, S. 2004 On the effects of lateral wall oscillations on a turbulent boundary layer. Exp. Therm. Fluid Sci. 29, 41–52.CrossRefGoogle Scholar
Schlatter, P., Örlü, R., Li, Q., Brethouwer, G., Fransson, J. H. M., Johansson, A. V., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to $R{e}_{\Theta } = 2500$ studied through simulation and experiment. Phys. Fluids 21, 051702.CrossRefGoogle Scholar
Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Skandaji, L. 1997 Étude de la structure d’une couche limite turbulente soumise à des oscillations transversales de la paroi. PhD thesis, École Centrale de Lyon.Google Scholar
Skote, M. 2011 Turbulent boundary layer flow subject to streamwise oscillation of spanwise wall-velocity. Phys. Fluids 23, 081703.CrossRefGoogle Scholar
Skote, M. 2012 Temporal and spatial transients in turbulent boundary layer flow over an oscillating wall. Intl J. Heat Fluid Flow 38, 1–12.CrossRefGoogle Scholar
Skote, M. & Henningson, D. S. 2002 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 471, 107–136.CrossRefGoogle Scholar
Touber, E. & Leschziner, M. A. 2012 Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. J. Fluid Mech. 693, 150–200.CrossRefGoogle Scholar
Trujillo, S. M., Bogard, D. G. & Ball, K. S. 1997 Turbulent boundary layer drag reduction using an oscillating wall. AIAA Paper 97-1870.CrossRefGoogle Scholar
Viotti, C., Quadrio, M. & Luchini, P. 2009 Streamwise oscillation of spanwise velocity at the wall of a channel for turbulent drag reduction. Phys. Fluids 21, 115109.CrossRefGoogle Scholar
Xu, C. X. & Huang, W. X. 2005 Transient response of Reynolds stress transport to spanwise wall oscillation in a turbulent channel flow. Phys. Fluids 17, 018101.CrossRefGoogle Scholar
Yudhistira, I. & Skote, M. 2011 Direct numerical simulation of a turbulent boundary layer over an oscillating wall. J. Turbul. 12 (9), 1–17.CrossRefGoogle Scholar