Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T07:40:53.190Z Has data issue: false hasContentIssue false
  • English
  • Français

Combined measurement of velocity and temperature in liquid metal convection

Published online by Cambridge University Press:  15 August 2019

Till Zürner Open the ORCID record for Till Zürner [Opens in a new window] ,
Felix Schindler ,
Tobias Vogt ,
Sven Eckert  and
Jörg Schumacher Open the ORCID record for Jörg Schumacher [Opens in a new window]
Till Zürner*
Affiliation:
Institute of Thermodynamics and Fluid Mechanics, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
Felix Schindler
Affiliation:
Department of Magnetohydrodynamics, Institute of Fluid Dynamics, Helmholtz-Zentrum Dresden – Rossendorf, Bautzner Landstraße 400, D-01328 Dresden, Germany
Tobias Vogt
Affiliation:
Department of Magnetohydrodynamics, Institute of Fluid Dynamics, Helmholtz-Zentrum Dresden – Rossendorf, Bautzner Landstraße 400, D-01328 Dresden, Germany
Sven Eckert
Affiliation:
Department of Magnetohydrodynamics, Institute of Fluid Dynamics, Helmholtz-Zentrum Dresden – Rossendorf, Bautzner Landstraße 400, D-01328 Dresden, Germany
Jörg Schumacher
Affiliation:
Institute of Thermodynamics and Fluid Mechanics, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

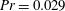Combined measurements of velocity components and temperature in a turbulent Rayleigh–Bénard convection flow at a low Prandtl number of $Pr=0.029$ and Rayleigh numbers of 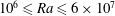$10^{6}\leqslant Ra\leqslant 6\times 10^{7}$ are conducted in a series of experiments with durations of more than a thousand free-fall time units. Multiple crossing ultrasound beam lines and an array of thermocouples at mid-height allow for a detailed analysis and characterization of the complex three-dimensional dynamics of the single large-scale circulation roll in a cylindrical convection cell of unit aspect ratio which is filled with the liquid metal alloy GaInSn. We measure the internal temporal correlations of the complex large-scale flow and distinguish between short-term oscillations associated with a sloshing motion in the mid-plane as well as varying orientation angles of the velocity close to the top/bottom plates and the slow azimuthal drift of the mean orientation of the roll as a whole that proceeds on a time scale up to a hundred times slower. The coherent large-scale circulation drives a vigorous turbulence in the whole cell that is quantified by direct Reynolds number measurements at different locations in the cell. The velocity increment statistics in the bulk of the cell displays characteristic properties of intermittent small-scale fluid turbulence. We also show that the impact of the symmetry-breaking large-scale flow persists to small-scale velocity fluctuations thus preventing the establishment of fully isotropic turbulence in the cell centre. Reynolds number amplitudes depend sensitively on beam-line position in the cell such that different definitions have to be compared. The global momentum and heat transfer scalings with Rayleigh number are found to agree with those of direct numerical simulations and other laboratory experiments.

JFM classification

Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 1108 - 1128
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.Google Scholar
Boggs, P. T. & Rogers, J. E. 1990 Orthogonal distance regression. In Statistical Analysis of Measurement Error Models and Applications, Contemporary Mathematics, vol. 112, pp. 183–194. American Mathematical Society.Google Scholar
Breuer, M., Wessling, S., Schmalzl, J. & Hansen, U. 2004 Effect of inertia in Rayleigh–Bénard convection. Phys. Rev. E 69 (2), 026302.Google Scholar
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.Google Scholar
Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.Google Scholar
Çengel, Y. A. 2008 Introduction to Thermodynamics and Heat Transfer, 2nd edn. McGraw-Hill Primis.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 58.Google Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Int. 166 (1), 97–114.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.Google Scholar
Franke, S., Lieske, H., Fischer, A., Büttner, L., Czarske, J. W., Räbiger, D. & Eckert, S. 2013 Two-dimensional ultrasound Doppler velocimeter for flow mapping of unsteady liquid metal flows. Ultrasonics 53 (3), 691–700.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume Motion and Large-Scale Circulation in a Cylindrical Rayleigh–Bénard Cell. Phys. Rev. Lett. 92 (19), 194502.Google Scholar
Glazier, J. A., Segawa, T., Naert, A. & Sano, M. 1999 Evidence against ‘ultrahard’ thermal turbulence at very high Rayleigh numbers. Nature 398, 307–310.Google Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14 (3), 1065–1081.Google Scholar
Hoyer, K., Holzner, M., Lüthi, B., Guala, M., Liberzon, A. & Kinzelbach, W. 2005 3D scanning particle tracking velocimetry. Exp. Fluids 39 (5), 923–934.Google Scholar
Kek, V. & Müller, U. 1993 Low Prandtl number convection in layers heated from below. Int. J. Heat Mass Transf. 36 (11), 2795–2804.Google Scholar
Kelley, D. H. & Weier, T. 2018 Fluid mechanics of liquid metal batteries. Appl. Mech. Rev. 70 (2), 020801.Google Scholar
Khalilov, R., Kolesnichenko, I., Pavlinov, A., Mamykin, A., Shestakov, A. & Frick, P. 2018 Thermal convection of liquid sodium in inclined cylinders. Phys. Rev. Fluids 3 (4), 043503.Google Scholar
King, E. M. & Aurnou, J. M. 2013 Turbulent convection in liquid metal with and without rotation. Proc. Natl Acad. Sci. USA 110 (17), 6688–6693.Google Scholar
King, E. M. & Aurnou, J. M. 2015 Magnetostrophic balance as the optimal state for turbulent magnetoconvection. Proc. Natl Acad. Sci. USA 112 (4), 990–994.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H., Geurts, B. J., van Bokhoven, L. J. A., Akkermans, R. A. D. & Verzicco, R. 2008 Numerical and experimental investigation of structure-function scaling in turbulent Rayleigh–Bénard convection. Phys. Rev. E 77 (1), 016302.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42 (1), 335–364.Google Scholar
Mashiko, T., Tsuji, Y., Mizuno, T. & Sano, M. 2004 Instantaneous measurement of velocity fields in developed thermal turbulence in mercury. Phys. Rev. E 69 (3), 036306.Google Scholar
Müller, U. & Bühler, L. 2001 Magnetofluiddynamics in Channels and Containers. Springer.Google Scholar
Plevachuk, Y., Sklyarchuk, V., Eckert, S., Gerbeth, G. & Novakovic, R. 2014 Thermophysical properties of the liquid Ga–In–Sn eutectic alloy. J. Chem. Engng Data 59 (3), 757–763.Google Scholar
Qiu, X.-L., Shang, X.-D., Tong, P. & Xia, K.-Q. 2004 Velocity oscillations in turbulent Rayleigh–Bénard convection. Phys. Fluids 16 (2), 412–423.Google Scholar
Qiu, X.-L. & Tong, P. 2001 Onset of coherent oscillations in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 87 (9), 094501.Google Scholar
Rossby, H. T. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36 (2), 309–335.Google Scholar
Salavy, J.-F., Boccaccini, L. V., Lässer, R. L., Meyder, R., Neuberger, H., Poitevin, Y., Rampal, G., Rigal, E., Zmitko, M. & Aiello, A. 2007 Overview of the last progresses for the European Test Blanket Modules projects. Fusion Engng Des. 82 (15), 2105–2112.Google Scholar
Scheel, J. D. & Schumacher, J. 2016 Global and local statistics in turbulent convection at low Prandtl numbers. J. Fluid Mech. 802, 147–173.Google Scholar
Scheel, J. D. & Schumacher, J. 2017 Predicting transition ranges to fully turbulent viscous boundary layers in low Prandtl number convection flows. Phys. Rev. Fluids 2 (12), 123501.Google Scholar
Schumacher, J., Bandaru, V., Pandey, A. & Scheel, J. D. 2016 Transitional boundary layers in low-Prandtl-number convection. Phys. Rev. Fluids 1 (8), 084402.Google Scholar
Schumacher, J., Götzfried, P. & Scheel, J. D. 2015 Enhanced enstrophy generation for turbulent convection in low-Prandtl-number fluids. Proc. Natl Acad. Sci. USA 112 (31), 9530–9535.Google Scholar
Schumacher, J. & Scheel, J. D. 2016 Extreme dissipation event due to plume collision in a turbulent convection cell. Phys. Rev. E 94 (4), 043104.Google Scholar
Shi, N., Emran, M. S. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 706, 5–33.Google Scholar
Spiegel, E. A. 1962 Thermal turbulence at very small Prandtl number. J. Geophys. Res. 67 (8), 3063–3070.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2011 Effect of plumes on measuring the large scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 23 (9), 095110.Google Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005 Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72 (2), 026302.Google Scholar
Sun, C., Zhou, Q. & Xia, K.-Q. 2006 Cascades of velocity and temperature fluctuations in buoyancy-driven thermal turbulence. Phys. Rev. Lett. 97 (14), 144504.Google Scholar
Takeda, Y. 1987 Measurement of velocity profile of mercury flow by ultrasound Doppler shift method. Nucl. Technol. 79 (1), 120–124.Google Scholar
Takeshita, T., Segawa, T., Glazier, J. A. & Sano, M. 1996 Thermal turbulence in mercury. Phys. Rev. Lett. 76 (9), 1465.Google Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41 (1), 375–404.Google Scholar
Tsuji, Y., Mizuno, T., Mashiko, T. & Sano, M. 2005 Mean wind in convective turbulence of mercury. Phys. Rev. Lett. 94 (3), 034501.Google Scholar
van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2013 Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 736, 177–194.Google Scholar
Vogt, T., Horn, S., Grannan, A. M. & Aurnou, J. M. 2018a Jump rope vortex in liquid metal convection. Proc. Natl Acad. Sci. USA 115 (50), 12674–12679.Google Scholar
Vogt, T., Ishimi, W., Yanagisawa, T., Tasaka, Y., Sakuraba, A. & Eckert, S. 2018b Transition between quasi-two-dimensional and three-dimensional Rayleigh–Bénard convection in a horizontal magnetic field. Phys. Rev. Fluids 3 (1), 013503.Google Scholar
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102 (4), 044503.Google Scholar
Xie, Y.-C., Wei, P. & Xia, K.-Q. 2013 Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection. J. Fluid Mech. 717, 322–346.Google Scholar
Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.Google Scholar
Supplementary material: File

Zürner et al. supplementary material

Zürner et al. supplementary material 1

Download Zürner et al. supplementary material(File)
File 78.7 KB