Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T07:15:14.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent structures in the inner part of a rough-wall channel flow resolved using holographic PIV

Published online by Cambridge University Press:  19 September 2012

Siddharth Talapatra  and
Joseph Katz
Siddharth Talapatra
Affiliation:
The Johns Hopkins University, Baltimore, MD 21218, USA
Joseph Katz*
Affiliation:
The Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

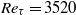Microscopic holographic PIV performed in an optically index-matched facility resolves the three-dimensional flow in the inner part of a turbulent channel flow over a rough wall at Reynolds number . The roughness consists of uniformly distributed pyramids with normalized height of 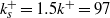. Distributions of mean flow and Reynolds stresses agree with two-dimensional PIV data except very close to the wall (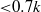) owing to the higher resolution of holography. Instantaneous realizations reveal that the roughness sublayer is flooded by low-lying spanwise and groove-parallel vortical structures, as well as quasi-streamwise vortices, some quite powerful, that rise at sharp angles. Conditional sampling and linear stochastic estimation (LSE) reveal that the prevalent flow phenomenon in the roughness sublayer consists of interacting U-shaped vortices, conjectured in Hong et al. (J. Fluid Mech., 2012, doi:10.1017/jfm.2012.403). Their low-lying base with primarily spanwise vorticity is located above the pyramid ridgeline, and their inclined quasi-streamwise legs extend between ridgelines. These structures form as spanwise vorticity rolls up in a low-speed region above the pyramid’s forward face, and is stretched axially by the higher-speed flow between ridgelines. Ejection induced by interactions among legs of vortices generated by neighbouring pyramids appears to be the mechanism that lifts the quasi-streamwise vortex legs and aligns them preferentially at angles of 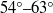to the streamwise direction.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 161 - 170
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
2. Adrian, R. J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.CrossRefGoogle Scholar
3. Antonia, R. A. & Luxton, R. E. 1971 The response of a turbulent boundary layer to a step change in surface roughness. Part 1. Smooth to rough. J. Fluid Mech. 48, 721–761.CrossRefGoogle Scholar
4. Finnigan, J. J., Shaw, R. H. & Patton, E. G. 2009 Turbulence structure above vegetation canopies. J. Fluid Mech. 637, 387–424.CrossRefGoogle Scholar
5. Hong, J., Katz, J., Meneveau, C. & Schultz, M. P. 2012 Coherent structures and associated subgrid-scale energy transfer in a rough-wall turbulent channel flow. J. Fluid Mech., doi:10.1017/jfm.2012.403.CrossRefGoogle Scholar
6. Hong, J., Katz, J. & Schultz, M. P. 2011 Near-wall turbulence statistics and flow structures over 3D roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.CrossRefGoogle Scholar
7. Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.CrossRefGoogle Scholar
8. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
9. Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
10. Jimenez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
11. Ligrani, P. M. & Moffat, R. J. 1986 Structure of transitionally rough and fully rough turbulent boundary layers. J. Fluid Mech. 162, 69–98.CrossRefGoogle Scholar
12. Monty, J. P., Allen, J. J., Lien, K. & Chong, M. S. 2011 Modification of the large-scale features of high Reynolds number wall turbulence by passive surface obtrusions. Exp. Fluids 51, 1755–1763.CrossRefGoogle Scholar
13. Raupach, M. R., Antonia, T. A. & Rajagopalan, S. 1991 Rough wall boundary layers. Appl. Mech. Rev. 44, 1–25.CrossRefGoogle Scholar
14. Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
15. Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21, 015104.CrossRefGoogle Scholar
16. Sheng, J., Malkiel, E. & Katz, J. 2006 Digital holographic microscope for measuring 3D particle distribution and motions. Appl. Opt. 45, 3893–3901.CrossRefGoogle ScholarPubMed
17. Sheng, J., Malkiel, E. & Katz, J. 2008 Using digital holographic microscopy for simultaneous measurements of 3D near wall velocity and wall shear stress in a turbulent boundary layer. Exp. Fluids 45, 1023–1035.CrossRefGoogle Scholar
18. Tachie, M. F., Bergstrom, D. J. & Balachandar, R. 2003 Roughness effects in low- open channel turbulent boundary layers. Exp. Fluids 35, 338–346.CrossRefGoogle Scholar
19. Talapatra, S. & Katz, J. 2012 Scope of microscopic inline digital holography for resolving the 3D flow in the roughness sublayer. Meas. Sci. Technol. (in press).Google Scholar
20. Yang, Q. & Wang, M. 2009 Computational study of roughness induced boundary-layer noise. AIAA J. 47, 2417–2429.CrossRefGoogle Scholar