Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-24T17:02:56.937Z Has data issue: true hasContentIssue false
  • English
  • Français

Closed equation model for cavity evolution in granular media

Published online by Cambridge University Press:  26 September 2024

Junsheng Zeng Open the ORCID record for Junsheng Zeng [Opens in a new window] ,
Baoqing Meng Open the ORCID record for Baoqing Meng [Opens in a new window] ,
Xiaoyan Ye Open the ORCID record for Xiaoyan Ye [Opens in a new window]  and
Baolin Tian
Junsheng Zeng
Affiliation:
School of Aeronautic Science and Engineering, Beihang University, Beijing, PR China Shanghai Zhangjiang Institute of Mathematics, Shanghai, PR China
Baoqing Meng*
Affiliation:
Institute of Mechanics, Chinese Academy of Sciences, Beijing, PR China
Xiaoyan Ye*
Affiliation:
Key Laboratory of Mechanics on Disaster and Environment in Western China, Ministry of Education, College of Civil Engineering and Mechanics, Lanzhou University, Lanzhou, PR China
Baolin Tian
Affiliation:
School of Aeronautic Science and Engineering, Beihang University, Beijing, PR China Shanghai Zhangjiang Institute of Mathematics, Shanghai, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

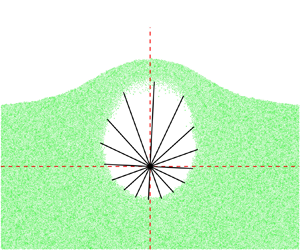
Cavity evolution in granular media is crucial in explosion-driven gas–particle flows, particularly in many engineering applications. In this study, a theoretical model was first proposed to describe the cavity evolution in granular media by extending the classical Rayleigh–Plesset model. A closed equation set comprising the radius, pressure and gas leak-off velocity equations was built by considering the gas expansion and non-Darcy gas-penetration effects. Both centrally symmetric and non-centrally symmetric cases of gas injection into granular media were investigated. Especially for modelling the non-symmetric scenario, the radius and gas leak-off velocity equations were proposed in each radial direction with angle $\theta$, and then the pressure equation was built up based on the integral gas leak-off along the cavity outline. Through non-dimensionalizing the theoretical equations, four key dimensionless numbers $\varPi_1,\ \varPi_4$ were obtained to characterize the response time of cavity expansion and the intensity of non-Darcy effects for both cases. This allowed us to determine a scaling law of effective cavity radius $R_{eff}^*=\sqrt {2\varPi _2/(7{\rm \pi} )}t^{*1/2}$ and the critical time $t_{cr}^*=\sqrt {12.5/\varPi _1}$ for two-dimensional cavity evolution. Additionally, the necessity of incorporating non-Darcy effects was ascertained under conditions of $\varPi _4>400$. The findings demonstrate that the proposed theoretical equations effectively predict the cavity evolution results under various operational conditions ($0.7<\varPi _1<7\times 10^2, 3<\varPi _4<1.1\times 10^3$), as validated by refined Euler–Lagrange numerical simulations.

JFM classification

Compressible Flows: Gas dynamics Drops and Bubbles: Bubble dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 996 , 10 October 2024 , A15
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anas, S.M., Alam, M. & Umair, M. 2022 Air-blast and ground shockwave parameters, shallow underground blasting, on the ground and buried shallow underground blast-resistant shelters: a review. Intl J. Protect. Struct. 13, 99–139.Google Scholar
Brennen, C.E. & Christopher, E. 2005 Fundamentals of Multiphase Flow, pp. 100–102. Cambridge University Press.Google Scholar
Devaraj, M. 2017 Impact on granular beds. Annu. Rev. Fluid Mech. 49, 463–484.Google Scholar
Ergun, S. 1952 Fluid flow through packed columns. Chem. Engng Prog. 48, 89–94.Google Scholar
Gao, M., Liu, X., Vanin, L.P., Sun, T.P., Cheng, X. & Gordillo, L. 2018 Dynamics and scaling of explosion cratering in granular media. AIChE J. 64, 2972–2981.Google Scholar
Housen, K.R. & Holsapple, K.A. 2003 Impact cratering on porous asteroids. Icarus 163, 102–119.Google Scholar
Jiang, N., Zhou, C., Lu, S. & Zhang, Z. 2017 Propagation and prediction of blasting vibration on slope in an open pit during underground mining. Tunnelling Underground Space Technol. 70, 409–421.Google Scholar
Koneru, R.B., Rollin, B., Durant, B., Ouellet, F. & Balachandar, S. 2020 A numerical study of particle jetting in a dense particle bed driven by an air-blast. Phys. Fluids 32, 093301.Google Scholar
Lai, S., Houim, R.W. & Oran, E.S. 2017 Mechanism and structure of subsurface explosions in granular media. Phys. Rev. Fluids 2, 094301.Google Scholar
Li, J., Xue, K., Zeng, J., Tian, B. & Guo, X. 2022 Shock-induced interfacial instabilities of granular media. J. Fluid Mech. 930, A22.Google Scholar
Liu, T., Cao, B., Liu, X., Sun, T. & Chen, X. 2020 Explosion cratering in 3D granular media. Soft Matt. 16, 1323–1332.Google Scholar
Lohse, D 2018 Bubble puzzles: from fundamentals to applications. Phys. Rev. Fluids 3, 111504.Google Scholar
Loranca-Ramos, F.E., Carrillo-Estrada, J.L. & Pacheco-Vázquez, F. 2015 Craters and granular jets generated by underground cavity collapse. Phys. Rev. Lett. 115, 028001.Google Scholar
Pacheco-Vázquez, F., Tacumá, A. & Marston, J.O. 2017 Craters produced by explosions in a granular medium. Phys. Rev. E 96, 032904.Google Scholar
Plesset, M.S. & Prosperetti, A. 1977 Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 9, 145–185.Google Scholar
Taylor, G. 1950 The formation of a blast wave by a very intense explosion. II. The atomic explosion of 1945. Proc. R. Soc. Lond. A 201, 175–186.Google Scholar
Tian, B., Zeng, J., Meng, B., Chen, Q., Guo, X. & Xue, K. 2020 Compressible multiphase particle-in-cell method (CMP-PIC) for full pattern flows of gas-particle system. J. Comput. Phys. 418, 109602.Google Scholar
Wang, J., Li, H., Guo, W., Wang, Z., Du, T., Wang, Y., Abe, A. & Huang, C. 2021 Rayleigh–Taylor instability of cylindrical water droplet induced by laser-produced cavitation bubble. J. Fluid Mech. 919, A42.Google Scholar
Xue, K., Miu, L., Li, J., Bai, C. & Tian, B. 2023 Explosive dispersal of granular media. J. Fluid Mech. 959, A17.Google Scholar
Zhang, A.M., Li, S.M., Cui, P., Li, S. & Liu, Y.L. 2023 A unified theory for bubble dynamics. Phys. Fluids 35, 033323.Google Scholar
Zhao, R., Zhang, Q., Tjugito, H. & Cheng, X. 2015 Granular impact cratering by liquid drops: understanding raindrop imprints through an analogy to asteroid strikes. Proc. Natl Acad. Sci. USA 112, 342–347.Google Scholar