Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T14:17:17.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Characteristic length scales of strongly rotating Boussinesq flow in variable-aspect-ratio domains

Published online by Cambridge University Press:  04 October 2018

X. M. Zhai  and
Susan Kurien Open the ORCID record for Susan Kurien [Opens in a new window]
X. M. Zhai
Affiliation:
School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
Susan Kurien*
Affiliation:
New Mexico Consortium, Los Alamos, NM 87544, USA Los Alamos National Laboratory, Theoretical Division, Los Alamos, NM 87545, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We quantify the variability of the characteristic length scales of isotropically forced Boussinesq flows with stratification and frame rotation, as functions of the ratio 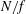$N/f$ of the Brunt–Väisälä frequency to the Coriolis frequency. The parameter ranges 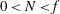$0<N<f$, domain aspect ratio 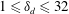$1\leqslant \unicode[STIX]{x1D6FF}_{d}\leqslant 32$ and Burger number 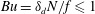$Bu=\unicode[STIX]{x1D6FF}_{d}N/f\leqslant 1$ are explored for two values of 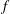$f$, one resulting in linear potential vorticity and the other in nonlinear potential vorticity. Characteristic length scales of the wave and vortical linear eigenmodes are separately quantified using $n$th-order spectral moments in both horizontal and vertical directions, for integer 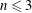$n\leqslant 3$. In flows with linear potential vorticity, the horizontal vortical length scale 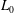$L_{0}$, characterizing a typical width of columnar structures, grows as 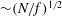${\sim}(N/f)^{1/2}$ at all orders of $n$, regardless of domain aspect ratio. In unit-aspect-ratio domains, when intermediate scales are measured by filtering out the largest scales and using higher-order moments 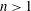$n>1$, the vortical-mode aspect ratio 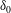$\unicode[STIX]{x1D6FF}_{0}$ asymptotes to a scaling of 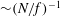${\sim}(N/f)^{-1}$, in agreement with quasi-geostrophic estimates. In contrast, the 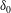$\unicode[STIX]{x1D6FF}_{0}$ in tall-aspect-ratio domain flows yields a decay rate of at most ${\sim}(N/f)^{-1/2}$ after large-scale filtering. Flows with nonlinear potential vorticity display consistently weaker dependence of the characteristic scales on 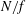$N/f$ than the corresponding ones with linear potential vorticity. The wave-mode aspect ratios for all flows are essentially independent of 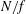$N/f$. We highlight the differences of these flow structure scalings relative to those expected for quasi-geostrophic flows, and those observed in strongly stratified, non-quasi-geostrophic flows.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 397 - 425
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aluie, H. & Kurien, S. 2011 Joint downscale fluxes of energy and potential enstrophy in rotating and stratified Boussinesq flows. Europhys. Lett. 96, 44006.Google Scholar
Aubert, O., Le Bars, M., Le Gal, P. & Marcus, P. S. 2012 The universal aspect ratio of vortices in rotating stratified flows: experiments and observations. J. Fluid Mech. 706, 34–45.Google Scholar
Babin, A. V., Mahalov, A. & Nicolaenko, B. 1995 Long-time averaged Euler and Navier–Stokes equations for rotating fluids. In Proceedings of the IUTAM/ISIMM Symposium on Structure and Dynamics of Nonlinear Waves in Fluids, Hanover, 1994 (ed. Kirchgässner, K. & Mielke, A.), Advanced Series in Nonlinear Dynamics, vol. 7, pp. 145–157. World Scientific.Google Scholar
Babin, A., Mahalov, A., Nicolaenko, B. & Zhou, Y. 1997 On the asymptotic regimes and the strongly stratified limit of rotating Boussinesq equations. Theor. Comput. Fluid Dyn. 9 (3/4), 223–251.Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.Google Scholar
Bartello, P., Metais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1–29.Google Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 16 (6), 1645–1651.Google Scholar
Cambon, C., Mansour, N. N. & Squires, K. D. 1994 Anisotropic structure of homogeneous turbulence subjected to uniform rotation. In Center for Turbulence Research, Proceedings of the Summer Program.Google Scholar
Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.Google Scholar
Chasnov, J. R. 1994 Similarity states of passive scalar transport in isotropic turbulence. Phys. Fluids 6 (2), 1036–1051.Google Scholar
Cushman-Roisin, B. 1994 Introduction to Geophysical Fluid Dynamics. Prentice-Hall.Google Scholar
Embid, P. & Majda, A. J. 1998 Low Froude number limiting dynamics for stably stratified flow with small or finite Rossby numbers. Geophys. Astrophys. Fluid Dyn. 87, 1–50.Google Scholar
Ertel, H. 1942 Ein neuer hydrodynamischer wirbelsatz. Met. Z. 59, 271–281.Google Scholar
Frisch, U., Kurien, S., Pandit, R., Pauls, W., Ray, S. S., Wirth, A. & Zhu, J.-Z. 2008 Hyperviscosity, galerkin-truncation and bottlenecks in turbulence. Phys. Rev. Lett. 101, 144501.Google Scholar
Godeferd, F. S. & Moisy, F. 2015 Structure and dynamics of rotating turbulence: a review of recent experimental and numerical results. Appl. Mech. Rev. 67, 030802.Google Scholar
Hassanzadeh, P., Marcus, P. S. & Le Gal, P. 2012 The universal aspect ratio of vortices in rotating stratified flows: theory and simulation. J. Fluid Mech. 706, 46–57.Google Scholar
Hough, S. S. 1897 On the application of harmonic analysis to the dynamical theory of the tides. Part I. On Laplace’s ‘oscillations of the first species,’ and on the dynamics of ocean currents. Phil. Trans. R. Soc. Lond. A 189, 201–257.Google Scholar
Ishihara, T., Morishita, K., Yokokawa, M., Uno, A. & Kaneda, Y. 2016 Energy spectrum in high-resolution direct numerical simulations of turbulence. Phys. Rev. Fluids 1, 082403.Google Scholar
Julien, K., Knobloch, E., Milliff, R. & Werne, J. 2006 Generalized quasi-geostrophy for spatially anisotropic rotationally constrained flows. J. Fluid Mech. 555, 233–274.Google Scholar
Kurien, S. & Smith, L. M. 2012 Asymptotics of unit Burger number rotating and stratified flows for small aspect-ratio. Physica D 241 (3), 149–163.Google Scholar
Kurien, S. & Smith, L. M. 2014 Effect of rotation and domain aspect-ratio on layer formation in strongly stratified Boussinesq flows. J. Turbul. 15 (4), 241–271.Google Scholar
Kurien, S., Smith, L. & Wingate, B. 2006 On the two-point correlation of potential vorticity in rotating and stratified turbulence. J. Fluid Mech. 555, 131–140.Google Scholar
Kurien, S. & Taylor, M. A. 2005 Direct numerical simulation of turbulence: data generation and statistical analysis. Los Alamos Sci. 29, 142–151.Google Scholar
Kurien, S., Wingate, B. & Taylor, M. A. 2008 Anisotropic constraints on energy distribution in rotating and stratified flows. Europhys. Lett. 84, 24003.Google Scholar
Liechtenstein, L., Godeferd, F. & Cambon, C. 2005 Nonlinear formation of structures in rotating, stratified turbulence. J. Turbul. 6, 1–18.Google Scholar
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40, 749–761.Google Scholar
Majda, A. J. 2003 Introduction to PDEs and Waves for the Atmosphere and Ocean, Courant Lecture Notes in Mathematics, vol. 9. New York University Courant Institute of Mathematical Sciences.Google Scholar
Marino, R., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2013 Inverse cascades in rotating stratified turbulence: Fast growth of large scales. Europhys. Lett. 102, 44006.Google Scholar
McWilliams, J. C. 1985 A note on a uniformly valid model spanning the regimes of geostrophic and isotropic, stratified turbulence: balanced turbulence. J. Atmos. Sci. 42, 1773–1774.Google Scholar
McWilliams, J. C., Molemaker, M. J. & Yavneh, I. 2004 Ageostrophic, anticyclonic instability of a geostrophic, barotropic boundary current. Phys. Fluids 16, 3720–3725.Google Scholar
McWilliams, J. C., Weiss, J. B. & Yavneh, I. 1999 The vortices of homogeneous geostrophic turbulence. J. Fluid Mech. 401, 1–26.Google Scholar
Nieves, D., Grooms, I., Julien, K. & Weiss, J. B. 2016 Investigations of non-hydrostatic, stably stratified and rapidly rotating flows. J. Fluid Mech. 801, 430–458.Google Scholar
Pedlosky, J. 1986 Geophysical Fluid Dynamics. Springer.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Praud, O., Fincham, A. M. & Sommeria, J. 2005 Decaying grid turbulence in a strongly stratified fluid. J. Fluid Mech. 522, 1–33.Google Scholar
Praud, O., Sommeria, J. & Fincham, A. M. 2006 Decaying grid turbulence in a rotating stratified fluid. J. Fluid Mech. 547, 389–412.Google Scholar
Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92, 408–424.Google Scholar
Remmel, M., Sukhatme, J. & Smith, L. M. 2010 Nonlinear inertia-gravity wave-mode interactions in three dimensional rotating stratified flows. Commun. Math. Sci. 8 (2), 357–376.Google Scholar
Rosenberg, D., Pouquet, A., Marino, R. & Minnini, P. D. 2015 Evidence for Bolgiano–Obukhov scaling in rotating stratified turbulence using high resolution direct numerical simulations. Phys. Fluids 27, 055105.Google Scholar
Smith, L. M., Chasnov, J. & Waleffe, F. 1996 Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 77, 2467–2470.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow, large scales in forced rotating, stratified turbulence. J. Fluid Mech. 451, 145–168.Google Scholar
Sukhatme, J. & Smith, L. M. 2008 Vortical and wave modes in 3d rotating stratified flows: Random large scale forcing. Geophys. Astrophys. Fluid Dyn. 102, 437–455.Google Scholar
Taylor, G. I. 1917 Motion of solids in fluids when the flow is not irrotational. Proc. R. Soc. Lond. A 93, 92–113.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar
Waite, M. L. 2013 Potential enstrophy in stratified turbulence. J. Fluid Mech. 722 (R4), 066602.Google Scholar
Waite, M. L. & Bartello, P. 2006 The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.Google Scholar
Wang, H. & George, W. K. 2002 The integral scale in homogeneous isotropic turbulence. J. Fluid Mech. 459, 429–443.Google Scholar
Wingate, B., Embid, P., Holmes-Cerfon, M. & Taylor, M. A. 2011 Low Rossby limiting dynamics for stably stratified flow with finite Froude number. J. Fluid Mech. 676, 546–571.Google Scholar