Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T13:27:04.847Z Has data issue: false hasContentIssue false
  • English
  • Français

Capillary waves control the ejection of bubble bursting jets

Published online by Cambridge University Press:  25 March 2019

J. M. Gordillo Open the ORCID record for J. M. Gordillo [Opens in a new window]  and
J. Rodríguez-Rodríguez
J. M. Gordillo*
Affiliation:
Grupo de Mecánica de Fluidos, Departamento de Ingeniería Aeroespacial y Mecánica de Fluidos, Universidad de Sevilla, Avenida de los Descubrimientos s/n 41092, Sevilla, Spain
J. Rodríguez-Rodríguez
Affiliation:
Grupo de Mecánica de Fluidos, Universidad Carlos III de Madrid, 28911, Leganés, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Here we provide a theoretical framework describing the generation of the fast jet ejected vertically out of a liquid when a bubble, resting on a liquid–gas interface, bursts. The self-consistent physical mechanism presented here explains the emergence of the liquid jet as a consequence of the collapse of the gas cavity driven by the low capillary pressures that appear suddenly around its base when the cap, the thin film separating the bubble from the ambient gas, pinches. The resulting pressure gradient deforms the bubble which, at the moment of jet ejection, adopts the shape of a truncated cone. The dynamics near the lower base of the cone, and thus the jet ejection process, is determined by the wavelength 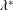$\unicode[STIX]{x1D706}^{\ast }$ of the smallest capillary wave created during the coalescence of the bubble with the atmosphere which is not attenuated by viscosity. The minimum radius at the lower base of the cone decreases, and hence the capillary suction and the associated radial velocities increase, with the wavelength 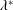$\unicode[STIX]{x1D706}^{\ast }$. We show that 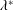$\unicode[STIX]{x1D706}^{\ast }$ increases with viscosity as 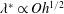$\unicode[STIX]{x1D706}^{\ast }\propto Oh^{1/2}$ for 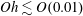$Oh\lesssim O(0.01)$, with 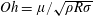$Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70C}R\unicode[STIX]{x1D70E}}$ the Ohnesorge number, 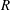$R$ the bubble radius and 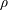$\unicode[STIX]{x1D70C}$, 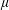$\unicode[STIX]{x1D707}$ and $\unicode[STIX]{x1D70E}$ indicating respectively the liquid density, viscosity and interfacial tension coefficient. The velocity of the extremely fast and thin jet can be calculated as the flow generated by a continuous line of sinks extending along the axis of symmetry a distance proportional to 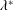$\unicode[STIX]{x1D706}^{\ast }$. We find that the jet velocity increases with the Ohnesorge number and reaches a maximum for 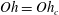$Oh=Oh_{c}$, the value for which the crest of the capillary wave reaches the vertex of the cone, and which depends on the Bond number 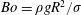$Bo=\unicode[STIX]{x1D70C}gR^{2}/\unicode[STIX]{x1D70E}$. For 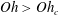$Oh>Oh_{c}$, the jet is ejected after a bubble is pinched off; in this regime, viscosity delays the formation of the jet, which is thereafter emitted at a velocity which is inversely proportional to the liquid viscosity.

JFM classification

Drops and Bubbles: Aerosols/atomization Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Bubble dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 556 - 571
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bigg, K. E. & Leck, C. 2008 The composition of fragments of bubbles bursting at the ocean surface. J. Geophys. Res. 4113, D11209.Google Scholar
Birkhoff, G., MacDougall, D. P., Pugh, E. M. & Taylor, S. G. 1948 Explosives with lined cavities. J. Appl. Phys. 19 (6), 563–582.Google Scholar
Crapper, G. D. 1957 An exact solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 2, 532–540.Google Scholar
Deike, L., Ghabache, E., Liger-Belair, G., Das, A. K., Zaleski, S., Popinet, S. & Seon, T. 2018 Dynamics of jets produced by bursting bubbles. Phys. Rev. Fluids 3, 013603.Google Scholar
Duchemin, L., Popinet, S., Josserand, C. & Zaleski, S. 2002 Jet formation in bubbles bursting at a free surface. Phys. Fluids 14, 3000–3008.Google Scholar
Eggers, J. & Villermaux, E. 2008 Physics of liquid jets. Rep. Prog. Phys. 71 (3), 036601.Google Scholar
Gañán Calvo, A. M. 2017 Revision of bubble bursting: universal scaling laws of top jet drop size and speed. Phys. Rev. Lett. 119, 204502.Google Scholar
Gañán Calvo, A. M. 2018 Scaling laws of top jet drop size and speed from bubble bursting including gravity and inviscid limit. Phys. Rev. Fluids 3, 091601.Google Scholar
Gekle, S. & Gordillo, J. M. 2010 Generation and breakup of worthington jets after cavity collapse. Part 1. Jet formation. J. Fluid Mech. 663, 293–330.Google Scholar
Gekle, S., Gordillo, J. M., van der Meer, D. & Lohse, D. 2009 High-speed jet formation after solid object impact. Phys. Rev. Lett. 102, 034502.Google Scholar
Ghabache, E., Antkowiak, A., Josserand, C. & Seon, T. 2014 On the physics of fizziness: how bubble bursting controls droplets ejection. Phys. Fluids 26, 121701.Google Scholar
Ghabache, E., Liger-Belair, G., Antkowiak, A. & Seon, T. 2016 Evaporation of droplets in a champagne wine aerosol. Sci. Rep. 6, 25148.Google Scholar
Ghabache, E. & Seon, T. 2016 Size of the top jet drop produced by bubble bursting. Phys. Rev. Fluids 1, 051901(R).Google Scholar
Gilet, T., Mulleners, K., Lecomte, J. P., Vandewalle, N. & Dorbolo, S. 2007 Critical parameters for the partial coalescence of a droplet. Phys. Rev. E 75, 036303.Google Scholar
Gordillo, J. M. 2008 Axisymmetric bubble collapse in a quiescent liquid pool. I. Theory and numerical simulations. Phys. Fluids 20 (11), 112103.Google Scholar
Gordillo, J. M. & Rodríguez-Rodríguez, Javier 2018 Comment on revision of bubble bursting: universal scaling laws of top jet drop size and speed. Phys. Rev. Lett. 121, 269401.Google Scholar
Krishnan, S., Hopfinger, E. J. & Puthenveettil, B. A. 2017 On the scaling of jetting from bubble collapse at a liquid surface. J. Fluid Mech. 822, 791–812.Google Scholar
Lai, C.-Y., Eggers, J. & Deike, L. 2018 Bubble bursting: universal cavity and jet profiles. Phys. Rev. Lett. 121, 144501.Google Scholar
de Leeuw, G., Andreas, E. L., Anguelova, M. D., Fairall, C. W., Lewis, E. R., O’Dowd, C., Schulz, M. & Schwartz, S. E. 2011 Production flux of sea spray aerosol. Rev. Geophys. 49, 2010RG000349.Google Scholar
Lhuissier, H. & Villermaux, E. 2012 Bursting bubble aerosol. J. Fluid Mech. 696, 5–44.Google Scholar
MacIntyre, F. 1972 Flow patterns in breaking bubbles. J. Geophys. Res. 77, 5211–5225.Google Scholar
Moore, D. W. 1963 The boundary layer on a spherical gas bubble. J. Fluid Mech. 16, 161–176.Google Scholar
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190 (2), 572–600.Google Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113, 024507.Google Scholar
Sierou, A. & Lister, J. R. 2004 Self-similar recoil of inviscid drops. Phys. Fluids 16, 1379–1394.Google Scholar
Song, M. & Tryggvason, G. 1999 The formation of thick borders on an initially stationary fluid sheet. Phys. Fluids 11, 2487–2493.Google Scholar
Spiel, D. E. 1998 On the births of film drops from bubbles bursting on seawater surfaces. J. Geophys. Res. 103, 907–918.Google Scholar
Taylor, G. I. 1959 The dynamics of thin sheets of fluid. III. Desintegration of fluid sheets. Proc. R. Soc. Lond. A 253, 313–321.Google Scholar
Thoroddsen, S. T., Takehara, K., Nguyen, H. D. & Etoh, T. G. 2018 Singular jets during the collapse of drop-impact craters. J. Fluid Mech. 848, R3.Google Scholar
Veron, F. 2015 Ocean spray. Annu. Rev. Fluid Mech. 47, 507–538.Google Scholar
Walls, P. L. L., Bird, J. C. & Bourouiba, L. 2014 Moving with bubbles: a review of the interactions between bubbles and the microorganisms that surround them. Integr. Compar. Biol. 54, 1014–1025.Google Scholar
Walls, P. L. L., Henaux, L. & Bird, J. C. 2015 Jet drops from bursting bubbles: how gravity and viscosity couple to inhibit droplet production. Phys. Rev. E 92, 021002(R).Google Scholar
Worthington, A. M. & Cole, R. S. 1896 Impact with a liquid surface, studies by the aid of instantaneous photography. Phil. Trans. R. Soc. Lond A 189, 137–148.Google Scholar
Zeff, B. W., Kleber, B., Fineberg, J. & Lathrop, D. P. 2000 Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature 403, 401–404.Google Scholar
Zhang, F. H., Thoraval, M.-J., Thoroddsen, S. T. & Taborek, P. 2015 Partial coalescence from bubbles to drops. J. Fluid Mech. 782, 209–239.Google Scholar

Gordillo and Rodríguez-Rodríguez supplementary movie 1

Bursting of a bubble for Bo=0.05 and Oh=0.004. The movie shows the time evolution of the bubble interface between t=0 and t=0.6. The time interval between frames is dt=0.01. This movie corresponds to a case in the low Ohnesorge regime Oh<

Download Gordillo and Rodríguez-Rodríguez supplementary movie 1(Video)
Video 853.3 KB

Gordillo and Rodríguez-Rodríguez supplementary movie 2

Bursting of a bubble for Bo=0.05 and Oh=0.02. The movie shows the time evolution of the interface between t=0 and t=0.6. The time interval between frames is dt=0.01. This movie corresponds to a case in which Oh\approx Oh_c

Download Gordillo and Rodríguez-Rodríguez supplementary movie 2(Video)
Video 816.6 KB

Gordillo and Rodríguez-Rodríguez supplementary movie 3

Bursting of a bubble for Bo=0.05 and Oh=0.04. The movie shows the time evolution of the interface between t=0 and t=0.6. The time interval between frames is dt=0.01. This movie corresponds to a case in which Oh>Oh_c

Download Gordillo and Rodríguez-Rodríguez supplementary movie 3(Video)
Video 801.6 KB