Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T02:23:53.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Breakup of a conducting drop in a uniform electric field

Published online by Cambridge University Press:  11 August 2014

Rahul B. Karyappa ,
Shivraj D. Deshmukh  and
Rochish M. Thaokar
Rahul B. Karyappa
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400 076, India
Shivraj D. Deshmukh
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400 076, India
Rochish M. Thaokar*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400 076, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

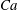A conducting drop suspended in a viscous dielectric and subjected to a uniform DC electric field deforms to a steady-state shape when the electric stress and the viscous stress balance. Beyond a critical electric capillary number $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ca}$, which is the ratio of the electric to the capillary stress, a drop undergoes breakup. Although the steady-state deformation is independent of the viscosity ratio 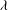$\lambda $ of the drop and the medium phase, the breakup itself is dependent upon 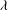$\lambda $ and 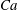$\mathit{Ca}$. We perform a detailed experimental and numerical analysis of the axisymmetric shape prior to breakup (ASPB), which explains that there are three different kinds of ASPB modes: the formation of lobes, pointed ends and non-pointed ends. The axisymmetric shapes undergo transformation into the non-axisymmetric shape at breakup (NASB) before disintegrating. It is found that the lobes, pointed ends and non-pointed ends observed in ASPB give way to NASB modes of charged lobes disintegration, regular jets (which can undergo a whipping instability) and open jets, respectively. A detailed experimental and numerical analysis of the ASPB modes is conducted that explains the origin of the experimentally observed NASB modes. Several interesting features are reported for each of the three axisymmetric and non-axisymmetric modes when a drop undergoes breakup.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Drops and Bubbles: Electrohydrodynamic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 754 , 10 September 2014 , pp. 550 - 589
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajayi, O. O. 1978 A note on Taylor’s electrohydrodynamic theory. Proc. R. Soc. Lond. A 364, 499–507.Google Scholar
Allan, R. S. & Mason, S. G. 1962 Particle behaviour in shear and electric fields I. Deformation and burst of fluid drops. Proc. R. Soc. Lond. A 267, 45–61.Google Scholar
Aryafar, H. & Kavehpour, H. P. 2009 Electrocoalescence: effects of DC electric fields on coalescence of drops at planar interfaces. Langmuir 25, 12460–12465.CrossRefGoogle ScholarPubMed
Aryafar, H. & Kavehpour, H. P. 2010 Electrocoalescence fireworks. Phys. Fluids 22, 091103.Google Scholar
Basaran, O. A. & Scriven, L. E. 1989 Axisymmetric shapes and stability of charged drops in an external electric field. Phys. Fluids A 1, 799–809.Google Scholar
Baygents, J. C., Rivette, N. J. & Stone, H. A. 1998 Electrohydrodynamic deformation and interaction of drop pairs. J. Fluid Mech. 368 (1), 359–375.Google Scholar
Betelú, S. I., Fontelos, M. A., Kindelán, U. & Vantzos, O. 2006 Singularities on charged viscous droplets. Phys. Fluids 18, 051706.Google Scholar
Collins, R. T., Jones, J. J., Harris, M. T. & Basaran, O. A. 2008 Electrohydrodynamic tip streaming and emission of charged drops from liquid cones. Nat. Phys. 4, 149–154.Google Scholar
Deshmukh, S. D. & Thaokar, R. M. 2012 Deformation, breakup and motion of a perfect dielectric drop in a quadrupole electric field. Phys. Fluids 24, 032105.Google Scholar
Deshmukh, S. D. & Thaokar, R. M. 2013 Deformation and breakup of a leaky dielectric drop in a quadrupole electric field. J. Fluid Mech. 731, 713–733.Google Scholar
Dubash, N. & Mestel, A. J. 2007a Behaviour of a conducting drop in a highly viscous fluid subject to an electric field. J. Fluid Mech. 581, 469–493.CrossRefGoogle Scholar
Dubash, N. & Mestel, A. J. 2007b Breakup behavior of a conducting drop suspended in a viscous fluid subject to an electric field. Phys. Fluids 19, 072101.Google Scholar
Duft, D., Achtzehn, T., Mueller, R., Huber, B. A. & Leisner, T. 2003 Rayleigh jets from levitated droplets. Nature 421, 128.CrossRefGoogle Scholar
Eow, J. W. & Ghadiri, M. 2003 Motion, deformation and break-up of aqueous drops in oils under high electric field strengths. Chem. Engng Process 42, 259–272.Google Scholar
Eow, J. W., Ghadiri, M. & Sharif, A. 2001 Deformation and break-up of aqueous drops in dielectric liquids in high electric fields. J. Electrostat. 51–52, 463–469.CrossRefGoogle Scholar
Feng, J. Q. & Scott, T. C. 1996 A computation analysis of electrohydrodynamics of a leaky dielectric drop in an electric field. J. Fluid Mech. 311, 289–326.Google Scholar
Fenn, J. B., Mann, M., Meng, C. K., Wong, S. F. & Whitehouse, C. M. 1989 Electrospray ionization for mass-spectrometry of large biomolecules. Science 246, 64–71.Google Scholar
Garton, C. G. & Krasucki, Z. 1964 Bubbles in insulating liquids: stability in an electric field. Proc. R. Soc. Lond. A 280, 211–226.Google Scholar
Grimm, R. L. & Beauchamp, J. L. 2005 Dynamics of field-induced droplet ionization: time-resolved studies of distortion, jetting, and progeny formation from charged and neutral methanol droplets exposed to strong electric fields. J. Phys. Chem. B 109, 8244–8250.CrossRefGoogle ScholarPubMed
Ha, J.-W. & Yang, S.-M. 2000 Deformation and breakup of Newtonian and non-Newtonian conducting drops in an electric field. J. Fluid Mech. 405, 131–156.Google Scholar
Hadamard, J. S. 1911 Mouvement permanent lent d’une sphère liquide et visqueuse dans un liquide visqueux. C. R. Acad. Sci. 152, 1735–1752.Google Scholar
Lac, E. & Homsy, G. M. 2007 Axisymmetric deformation and stability of a viscous drop in a steady electric field. J. Fluid Mech. 590, 239–264.Google Scholar
Lewis, D. J. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Proc. R. Soc. Lond. A 202 (1068), 81–96.Google Scholar
Mhatre, S., Deshmukh, S. & Thaokar, R. 2012 Stability of a charged drop near a conductor wall. Eur. Phys. J. E 35 (5), 39.Google Scholar
Miksis, M. J. 1981 Shape of a drop in an electric field. Phys. Fluids 24, 1967–1972.Google Scholar
Moriya, S., Adachi, K. & Kotaka, T. 1986 Deformation of droplets suspended in viscous media in an electric field 1: rate of deformation. Langmuir 2, 155–160.Google Scholar
Mukherjee, S. & Sarkar, K. 2011 Viscoelastic drop falling through a viscous medium. Phys. Fluids 23, 013101.Google Scholar
Ochs, H. T. & Czys, R. R. 1987 Charge effects on the coalescence of water drops in free-fall. Nature 327, 606–608.Google Scholar
Park, J.-U., Hardy, M., Kang, S. J., Barton, K., Adair, K., Mukhopadhyay, D. K., Lee, C. Y., Strano, M. S., Alleyne, A. G., Georgiadis, J. G., Ferreira, P. M. & Rogers, J. A. 2007 High-resolution electrohydrodynamic jet printing. Nat. Mater. 6, 782–789.Google Scholar
Pozrikidis, C. 1990a The deformation of a liquid drop moving normal to a plane wall. J. Fluid Mech. 215, 331–363.CrossRefGoogle Scholar
Pozrikidis, C. 1990b The instability of a moving viscous drop. J. Fluid Mech. 210, 1–21.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Ramos, A. & Castellanos, A. 1994 Conical points in liquid–liquid interfaces subjected to electric fields. Phys. Lett. A 184, 268–272.Google Scholar
Rayleigh, Lord 1882 On the equilibrium of liquid conducting masses charged with electricity. Phil. Mag. 14, 184–186.Google Scholar
Reznik, S. N., Yarin, A. L., Theron, A. & Zussman, E. 2004 Transient and steady shapes of droplets attached to a surface in a strong electric field. J. Fluid Mech. 516, 349–377.Google Scholar
Rybczynski, W. 1911 Über die fortschreitende Bewegung einer flüssigen Kugel in einem zähen Medium. Bull. Acad. Sci. Cracov. Ser. A 1, 40–46.Google Scholar
Saffman, P. G. & Taylor, G. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245 (1242), 312–329.Google Scholar
Sherwood, J. D. 1988 Breakup of fluid droplets in electric and magnetic fields. J. Fluid Mech. 188, 133–146.Google Scholar
Stone, H. A. 1994 Dynamics of drop deformation and breakup in viscous fluids. Annu. Rev. Fluid Mech. 26, 65–102.CrossRefGoogle Scholar
Stone, H. A., Lister, J. R. & Brenner, M. P. 1999 Drops with conical ends in electric and magnetic fields. Proc. R. Soc. Lond. A 455, 329–347.Google Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Proc. R. Soc. Lond. A 201 (1065), 192–196.Google Scholar
Taylor, G. I. 1964 Disintegration of water drops in an electric field. Proc. R. Soc. Lond. A 280, 383–397.Google Scholar
Taylor, G. I. 1966 Studies in electrohydrodynamics I. The circulation produced in a drop by an electric field. Proc. R. Soc. Lond. A 291, 159–166.Google Scholar
Torza, S., Cox, R. G. & Mason, S. G. 1971 Electrohydrodynamic deformation and burst of liquid drops. Phil. Trans. R. Soc. Lond. A 269, 295–319.Google Scholar
Varshney, A., Ghosh, S., Bhattacharya, S. & Yethiraj, A. 2012 Self organization of exotic oil-in-oil phases driven by tunable electrohydrodynamics. Sci. Rep. 2, 738.Google Scholar
Vizika, O. & Saville, D. A. 1992 The electrohydrodynamic deformation of drops suspended in liquids in steady and oscillatory electric fields. J. Fluid Mech. 239, 1–21.Google Scholar
Wilson, C. T. R. & Taylor, G. I. 1925 The bursting of soap bubbles in a uniform electric field. Proc. Camb. Phil. Soc. 22, 728–730.Google Scholar

Karyappa et al. supplementary movie

Breakup of a water drop suspended in castor oil (figure 10): (a, Ca, λ) = (112 μm, 0.40, 0.00126).

Download Karyappa et al. supplementary movie(Video)
Video 1.2 MB

Karyappa et al. supplementary movie

Regular jet breakup mode of a conducting drop for high viscosity ratio (figure 18(a)): (a, Ca, λ) = (190 μm , 0.30, 2.0).

Download Karyappa et al. supplementary movie(Video)
Video 1 MB

Karyappa et al. supplementary movie

Effect of electric capillary number Ca on the breakup mode (figure 19(a)): (a, Ca, λ) = (116 μm, 0.25, 0.575). At low Ca, a drop undergoes ASPB pointed ends breakup mode followed by NASB regular jet mode.

Download Karyappa et al. supplementary movie(Video)
Video 1.2 MB

Karyappa et al. supplementary movie

Effect of electric capillary number Ca on the breakup mode (figure 19(c)): (a, Ca, λ) = (105 μm, 1.1, 0.575). At high Ca, a drop undergoes ASPB pointed ends breakup mode followed by NASB open jet mode.

Download Karyappa et al. supplementary movie(Video)
Video 1.3 MB