Published online by Cambridge University Press: 15 September 2021
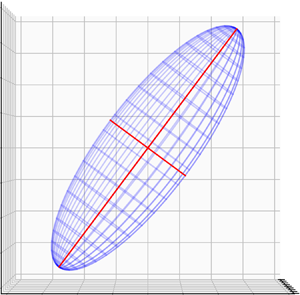
We consider a uniform ellipsoid of potential vorticity (PV), where we exploit analytical solutions derived for a balanced model at the second order in the Rossby number, the next order to quasi-geostrophic (QG) theory, the so-called QG+1 model. We consider this vortex in the presence of an external background shear flow, acting as a proxy for the effect of external vortices. For the QG model the system depends on four parameters, the height-to-width aspect ratio of the vortex,  $h/r$, as well as three parameters characterising the background flow, the strain rate,
$h/r$, as well as three parameters characterising the background flow, the strain rate,  $\gamma$, the ratio of the background rotation rate to the strain,
$\gamma$, the ratio of the background rotation rate to the strain,  $\beta$, and the angle from which the flow is applied,
$\beta$, and the angle from which the flow is applied,  $\theta$. However, the QG+1 model also depends on the PV, as well as the Prandtl ratio,
$\theta$. However, the QG+1 model also depends on the PV, as well as the Prandtl ratio,  $f/N$ (
$f/N$ ( $f$ and
$f$ and  $N$ are the Coriolis and buoyancy frequencies, respectively). For QG and QG+1 we determine equilibria for different values of the background flow parameters for increasing values of the imposed strain rate up to the critical strain rate,
$N$ are the Coriolis and buoyancy frequencies, respectively). For QG and QG+1 we determine equilibria for different values of the background flow parameters for increasing values of the imposed strain rate up to the critical strain rate,  $\gamma _c$, beyond which equilibria do not exist. We also compute the linear stability of this vortex to second-order modes, determining the marginal strain
$\gamma _c$, beyond which equilibria do not exist. We also compute the linear stability of this vortex to second-order modes, determining the marginal strain  $\gamma _m$ at which ellipsoidal instability erupts. The results show that for QG+1 the most resilient cyclonic ellipsoids are slightly prolate, while anticyclonic ellipsoids tend to be more oblate. The highest values of
$\gamma _m$ at which ellipsoidal instability erupts. The results show that for QG+1 the most resilient cyclonic ellipsoids are slightly prolate, while anticyclonic ellipsoids tend to be more oblate. The highest values of  $\gamma _m$ occur as
$\gamma _m$ occur as  $\beta \to 1$. For large values of
$\beta \to 1$. For large values of  $f/N$, changes in the marginal strain rates occur, stabilising anticyclonic ellipsoids while destabilising cyclonic ellipsoids.
$f/N$, changes in the marginal strain rates occur, stabilising anticyclonic ellipsoids while destabilising cyclonic ellipsoids.