Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-03T01:29:01.530Z Has data issue: false hasContentIssue false
  • English
  • Français

Axisymmetric spreading of surfactant from a point source

Published online by Cambridge University Press:  30 October 2017

Shreyas Mandre Open the ORCID record for Shreyas Mandre [Opens in a new window]
Shreyas Mandre*
Affiliation:
School of Engineering, Brown University, Providence, RI 02912, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Guided by computation, we theoretically calculate the steady flow driven by the Marangoni stress due to a surfactant introduced on a fluid interface at a constant rate. Two separate extreme cases, where the surfactant dynamics is dominated by the adsorbed phase or the dissolved phase, are considered. We focus on the case where the size of the surfactant source is much smaller than the size of the fluid domain, and the resulting Marangoni stress overwhelms the viscous forces so that the flow is strongest in a boundary layer close to the interface. We derive the resulting flow in a region much larger than the surfactant source but smaller than the domain size by approximating it with a self-similar profile. The radially outward component of fluid velocity decays with the radial distance $r$ as 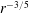$r^{-3/5}$ when the surfactant spreads in an adsorbed phase, and as 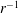$r^{-1}$ when it spreads in a dissolved phase. Universal flow profiles that are independent of the system parameters emerge in both the cases. Three hydrodynamic signatures are identified to distinguish between the two cases and verify the applicability of our analysis with successive stringent tests.

JFM classification

Convection: Convection Convection: Marangoni convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 777 - 792
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, vol. 55. Courier Corporation.Google Scholar
Bandi, M. M., Akella, V. S., Singh, D. K., Singh, R. S. & Mandre, S.2017 Hydrodynamic signatures of stationary Marangoni-driven surfactant transport. arXiv:1705.02873.Google Scholar
Bratukhin, I. K. & Maurin, L. N. 1967 Thermocapillary convection in a fluid filling a half-space: PMM vol. 31 no. 3, 1967, 577–580. Z. Angew. Math. Mech. J. Appl. Math. Mech. 31 (3), 605–608.Google Scholar
Bratukhin, Y. K. & Maurin, L. N. 1968 Dissolution of a hot body in contact with a free liquid surface. J. Engng Phys. Thermophys. 14 (6), 533–535.Google Scholar
Carpenter, B. M. & Homsy, G. M. 1990 High Marangoni number convection in a square cavity: part II. Phys. Fluids A 2 (2), 137–149.CrossRefGoogle Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81 (3), 1131–1198.CrossRefGoogle Scholar
Dukhin, S. S., Kretzschmar, G. & Miller, R. 1995 Dynamics of Adsorption at Liquid Interfaces: Theory, Experiment, Application, vol. 1. Elsevier.Google Scholar
Eastoe, J. & Dalton, J. S. 2000 Dynamic surface tension and adsorption mechanisms of surfactants at the air–water interface. Adv. Colloid Interface Sci. 85 (2), 103–144.Google Scholar
Jensen, O. E. 1995 The spreading of insoluble surfactant at the free surface of a deep fluid layer. J. Fluid Mech. 293, 349–378.Google Scholar
Le Roux, S., Roché, M., Cantat, I. & Saint-Jalmes, A. 2016 Soluble surfactant spreading: how the amphiphilicity sets the Marangoni hydrodynamics. Phys. Rev. E 93 (1), 013107.Google ScholarPubMed
Napolitano, L. G. 1979 Marangoni boundary layers. In Proceedings of 3rd European Symposium on Material Sciences in Space, vol. SP‐142, pp. 349–358. ESA.Google Scholar
Noskov, B. A. 1996 Fast adsorption at the liquid–gas interface. Adv. Colloid Interface Sci. 69 (1–3), 63–129.CrossRefGoogle Scholar
Roché, M., Li, Z., Griffiths, I. M., Le Roux, S., Cantat, I., Saint-Jalmes, A. & Stone, H. A. 2014 Marangoni flow of soluble amphiphiles. Phys. Rev. Lett. 112 (20), 208302.Google Scholar
Squire, H. B. 1955 Radial jets. In Fifty Years of Boundary Layer Research, pp. 47–54. Vieweg.Google Scholar
Xu, K., Booty, M. R. & Siegel, M. 2013 Analytical and computational methods for two-phase flow with soluble surfactant. SIAM J. Appl. Maths 73 (1), 523–548.Google Scholar
Young, Y.-N., Booty, M. R., Siegel, M. & Li, J. 2009 Influence of surfactant solubility on the deformation and breakup of a bubble or capillary jet in a viscous fluid. Phys. Fluids 21 (7), 072105.CrossRefGoogle Scholar
Zebib, A., Homsy, G. M. & Meiburg, E. 1985 High Marangoni number convection in a square cavity. Phys. Fluids 28 (12), 3467–3476.CrossRefGoogle Scholar