Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T13:59:32.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic scaling laws and semi-similarity solutions for a finite-source spherical blast wave

Published online by Cambridge University Press:  06 July 2018

Y. Ling Open the ORCID record for Y. Ling [Opens in a new window]  and
S. Balachandar Open the ORCID record for S. Balachandar [Opens in a new window]
Y. Ling*
Affiliation:
Department of Mechanical Engineering, Baylor University, Waco, TX 76798, USA
S. Balachandar
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A spherical blast wave generated by a sudden release of a sphere of compressed gas is an important model problem to understand blast phenomena such as volcanic eruptions and explosive detonations. The resulting explosion flow physics, such as the instability at the gas contact discontinuity and the interaction between the shock wave and the gas contact, are dictated by the initial pressure and sound-speed ratios between the compressed gas and the ambience. Since the initial pressure and sound-speed ratios vary over a wide range in practical applications, it is of interest to investigate the scaling laws and similarity solutions for the spherical symmetric explosion flow. In the present study, numerical simulation of a spherical blast wave is performed. A long-term length scale that incorporates the initial charge radius and the initial pressure ratio is introduced. The trajectories of the main shock normalized by the long-term length scale for a wide range of parameters collapse after a short transition time, indicating an asymptotic similarity solution exists for the far field in the long term. With the assistance of this similarity solution, the full evolution of the main shock can be obtained semi-analytically. For near-field features, i.e. the gas contact and the secondary shock wave, only semi-similarity solutions are observed, which depend on the initial sound-speed ratio but not the initial pressure ratio. The gas contact and the secondary shock share the same scaling relations. Asymptotic analysis is performed to obtain the short-term dynamics of the gas contact, including the gas contact acceleration and the Atwood number, which are the key parameters determining the Rayleigh–Taylor instability development at the gas contact. The asymptotic contact radius as 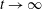$t\rightarrow \infty$ is also obtained, which is found to be well represented by the long-term length scale and thus only depends on the initial pressure ratio. A simple model of an oscillating bubble is employed to explain the scaling relation of the asymptotic gas contact radius.

JFM classification

Compressible Flows: Detonation waves Compressible Flows: Gas dynamics Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 674 - 707
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aref, H. & Balachandar, S. 2017 A First Course in Computational Fluid Dynamics. Cambridge University Press.Google Scholar
Balakrishnan, K. & Menon, S. 2010 On the role of ambient reactive particles in the mixing and afterburn behind explosive blast waves. Combust. Sci. Technol. 182, 186–214.Google Scholar
Balakrishnan, K. & Menon, S. 2011 A multiphase buoyancy-drag model for the study of Rayleigh–Taylor and Richtmyer–Meshkov instabilities in dusty gases. Laser Part. Beams 29, 201–217.Google Scholar
Balakrishnan, K., Nance, D. V. & Menon, S. 2010 Simulation of impulse effects from explosive charges containing metal particles. Shock Waves 20, 217–239.Google Scholar
Barth, T. J.1991, A 3D upwind Euler solver for unstructured meshes. AIAA Paper 91-1548.Google Scholar
Bell, G. I.1951 Taylor instability on cylinders and spheres in the small amplitude approximation. Report LA-1321. Los Alamos National Laboratory.Google Scholar
Boyer, D. W. 1960 An experimental study of the explosion generated by a pressurized sphere. J. Fluid Mech. 9, 401–429.Google Scholar
Brode, H. L. 1955 Numerical solutions of spherical blast waves. J. Appl. Phys. 26, 766–775.Google Scholar
Brode, H. L.1957 Theoretical solutions of spherical shock tube blasts. Tech. Rep. RM-1974. Rand Corporation Report.Google Scholar
Brode, H. L. 1959 Blast wave from a spherical charge. Phys. Fluids 2, 217–229.Google Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.Google Scholar
Chester, W. 1954 The quasi-cylindrical shock tube. Phil. Mag. 7, 1293–1301.Google Scholar
Chisnell, R. F. 1955 The normal motion of a shock wave through a non-uniform one-dimensional medium. Proc. R. Soc. Lond. A 232, 350–370.Google Scholar
Chisnell, R. F. 1957 The motion of a shock wave in a channel, with applications to cylindrical and spherical shock waves. J. Fluid Mech. 2, 286–298.Google Scholar
Epstein, R. 2004 On the Bell–Plesset effects: the effects of uniform compression and geometrical convergence on the classical Rayleigh–Taylor instability. Phys. Plasmas 11, 5114–5124.Google Scholar
Friedman, M. P. 1961 A simplified analysis of spherical and cylindrical blast waves. J. Fluid Mech. 11, 1–15.Google Scholar
Frost, D. L., Ornthanalai, C., Zarei, Z., Tanguay, V. & Zhang, F. 2007 Particle momentum effects from the detonation of heterogeneous explosives. J. Appl. Phys. 101, 113529.Google Scholar
Haselbacher, A.2005 A WENO reconstruction algorithm for unstructured grids based on explicit stencil construction. AIAA Paper 2005-0879.Google Scholar
Haselbacher, A., Balachandar, S. & Kieffer, S. W. 2007 Open-ended shock tube flows: Influence of pressure ratio and diaphragm position. AIAA J. 45 (8), 1917–1929.Google Scholar
Hayes, W. D. 1968 The propagation upward of the shock wave from a strong explosion in the atmosphere. J. Fluid Mech. 32, 317–331.Google Scholar
Igra, O., Elperin, T. & Ben-Dor, G. 1987 Blast waves in dusty gases. Proc. R. Soc. Lond. A 414, 197–219.Google Scholar
Jiang, G. S. & Shu, C. W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228.Google Scholar
Kato, K., Aoki, T., Kubota, S. & Yoshida, M. 2006 A numerical scheme for strong blast wave driven by explosion. Int. J. Numer. Meth. Fluids 51 (12), 1335–1353.Google Scholar
Liang, S.-M., Wang, J. S. & Chen, H. 2002 Numerical study of spherical blast-wave propagation and reflection. Shock Waves 12, 59–68.Google Scholar
Ling, Y., Haselbacher, A. & Balachandar, S. 2011a Importance of unsteady contributions to force and heating for particles in compressible flows. Part 1. Modeling and analysis for shock-particle interaction. Intl J. Multiphase Flow 37, 1026–1044.Google Scholar
Ling, Y., Haselbacher, A. & Balachandar, S. 2011b Importance of unsteady contributions to force and heating for particles in compressible flows. Part 2. Application to particle dispersal by blast wave. Intl J. Multiphase Flow 37, 1013–1025.Google Scholar
Ling, Y., Haselbacher, A., Balachandar, S., Najjar, F. M. & Stewart, D. S. 2013 Shock interaction with a deformable particle: direct numerical simulations and point-particle modeling. J. Appl. Phys. 113, 013504.Google Scholar
Ling, Y., Wagner, J. L., Beresh, S. J., Kearney, S. P. & Balachandar, S. 2012 Interaction of a planar shock wave with a dense particle curtain: modeling and experiments. Phys. Fluids 24, 113301.Google Scholar
Liu, T. G., Khoo, B. C. & Yeo, K. S. 1999 The numerical simulations of explosion and implosion in air: use of a modified Harten’s TVD scheme. Int. J. Numer. Meth. Fluids 31, 661–680.Google Scholar
Lutzky, M. & Lehto, D. L. 1970 Scaling of spherical blasts. J. Appl. Phys. 41, 844–846.Google Scholar
Mankbadi, M. R. & Balachandar, S. 2012 Compressible inviscid instability of rapidly expanding spherical material interfaces. Phys. Fluids 24 (3), 034106.Google Scholar
Mankbadi, M. R. & Balachandar, S. 2013 Viscous effects on the non-classical Rayleigh–Taylor instability of spherical material interfaces. Shock Waves 23, 603–617.Google Scholar
Mankbadi, M. R. & Balachandar, S. 2014 Multiphase effects on spherical Rayleigh–Taylor interfacial instability. Phys. Fluids 26, 023301.Google Scholar
McFadden, J. A. 1952 Initial behavior of a spherical blast. J. Appl. Phys. 23, 1269–1275.Google Scholar
Plesset, M. S. 1954 On the stability of fluid flows with spherical symmetry. J. Appl. Phys. 25, 96–98.Google Scholar
Plooster, M. N. 1970 Shock waves from line sources. Numerical solutions and experimental measurements. Phys. Fluids 13, 2665–2675.Google Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Roe, P. L. 1981 Approximate Riemann solver, parameter vectors, and difference schemes. J. Comput. Phys. 43, 357–372.Google Scholar
Sachdev, P. L. 2004 Shock Waves and Explosions. Chapman & Hall/CRC.Google Scholar
Sakurai, A. 1953 On the propagation and structure of the blast wave, i. J. Phys. Soc. Japan 8, 662–669.Google Scholar
Sedov, L. I. 1959 Similarity and Dimensional Methods in Mechanics. Academic Press.Google Scholar
Taylor, G. I. 1946 The air wave surrounding an expanding sphere. Proc. R. Soc. Lond. A 186, 273–292.Google Scholar
Taylor, G. I. 1950a The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Taylor, G. I. 1950b The formation of a blast wave by a very intense explosion. I. Theoretical discussion. Proc. R. Soc. Lond. A 201, 159–174.Google Scholar
Taylor, G. I. 1950c The formation of a blast wave by a very intense explosion. II. The atomic explosion of 1945. Proc. R. Soc. Lond. A 201, 175–186.Google Scholar
Tyas, A., Warren, J. A., Bennett, T. & Fay, S. 2011 Prediction of clearing effects in far-field blast loading of finite targets. Shock Waves 21, 111–119.Google Scholar
Ukai, S., Balakrishnan, K. & Menon, S. 2010 On Richtmyer-Meshkov instability in dilute gas-particle mixtures. Phys. Fluids 22, 104103.Google Scholar
Whitham, G. B. 1950 The propagation of spherical blast. Proc. R. Soc. Lond. A 203, 571–581.Google Scholar
Whitham, G. B. 1958 On the propagation of shock waves through regions of non-uniform area or flow. J. Fluid Mech. 4 (4), 337–360.Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar
Xu, T., Lien, F.-S., Ji, H. & Zhang, F. 2013 Formation of particle jetting in a cylindrical shock tube. Shock Waves 23, 619–634.Google Scholar
Zarei, Z. & Frost, D. L. 2011 Simplified modeling of blast waves from metalized heterogeneous explosives. Shock Waves 21, 425–438.Google Scholar
Zhang, F., Frost, D. L., Thibault, P. A. & Murray, S. B. 2001 Explosive dispersal of solid particles. Shock Waves 10, 431–443.Google Scholar