Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-30T00:13:33.774Z Has data issue: false hasContentIssue false
  • English
  • Français

Aspect-ratio effects on rotating wings: circulation and forces

Published online by Cambridge University Press:  20 February 2015

Zakery R. Carr ,
Adam C. DeVoria  and
Matthew J. Ringuette
Zakery R. Carr
Affiliation:
Department of Mechanical and Aerospace Engineering, University at Buffalo, The State University of New York, 318 Jarvis Hall, Buffalo, NY 14260-4400, USA
Adam C. DeVoria
Affiliation:
Department of Mechanical and Aerospace Engineering, University at Buffalo, The State University of New York, 318 Jarvis Hall, Buffalo, NY 14260-4400, USA
Matthew J. Ringuette*
Affiliation:
Department of Mechanical and Aerospace Engineering, University at Buffalo, The State University of New York, 318 Jarvis Hall, Buffalo, NY 14260-4400, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We employ experiments to study aspect ratio (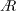$\def\AR{A\mkern-8muR}\AR$) effects on the vortex structure, circulation and lift force for flat-plate wings rotating from rest at 45° angle of attack, which represents a simplified hovering-wing half-stroke. We use the time-varying, volumetric 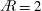$\AR =2$ data of Carr et al. (Exp. Fluids, vol. 54, 2013, pp. 1–26), reconstructed from phase-locked, phase-averaged stereoscopic digital particle image velocimetry (S-DPIV), and an 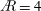$\AR =4$ volumetric data set matching the span-based Reynolds number (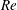$\mathit{Re}$) of 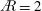$\AR =2$. For 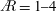$\AR =1{-}4$ and 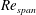$\mathit{Re}_{\mathit{span}}$ of 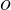$O$(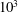$10^{3}$–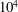$10^{4}$), we directly measure the lift force. The total leading-edge-region circulation for 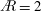$\AR =2$ and 4 compares best overall using a span-based normalization and for matching rotation angles. The total circulation increases across the span to the tip region, and is larger for 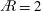$\AR =2$. After the startup, the total circulation for each 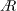$\AR$ has a similar slope and a slow growth. The first leading-edge vortex (LEV) and the tip vortex (TV) for 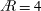$\AR =4$ move past the trailing edge, followed by substantial breakdown. For 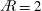$\AR =2$ the outboard, aft-tilted LEV merges with the TV and resides over the tip, although breakdown also occurs. Where the LEV is ‘stable’ inboard, its circulation saturates for 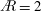$\AR =2$ and the growth slows for 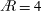$\AR =4$. Aft LEV tilting reduces the spanwise LEV circulation for each 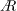$\AR$. Both positive and negative axial flow are found in the first LEV for 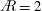$\AR =2$ and 4, with the positive component being somewhat larger. This yields a generally positive (outboard) average vorticity flux. The average lift coefficient is essentially constant with 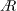$\AR$ from 1 to 4 during the slow growth phase, although the large-time behaviour shows a slight decrease in lift coefficient with increasing 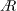$\AR$. The S-DPIV data are used to obtain the lift impulse and the spanwise and streamwise components contributing to the lift coefficient. The spanwise contribution is similar for 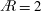$\AR =2$ and 4, due to similar trailing-edge vortex interactions, LEV saturation behaviour and total circulation slopes. However, for 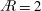$\AR =2$ the streamwise contribution is much larger, because of the stronger, coherent TV and aft-tilted LEV, which will create a relatively lower-pressure region over the tip.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 497 - 525
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: CUBRC, Inc., Buffalo, NY 14225, USA.

§

Present address: University of Florida, Gainesville, FL 32611, USA.

References

Ansari, S. A., Phillips, N., Stabler, G., Wilkins, P. C., Żbikowski, R. & Knowles, K. 2009 Experimental investigation of some aspects of insect-like flapping flight aerodynamics for application to micro air vehicles. Exp. Fluids 46, 777–798.Google Scholar
Carr, Z. R., Chen, C. & Ringuette, M. J. 2013a Finite-span rotating wings: three-dimensional vortex formation and variations with aspect ratio. Exp. Fluids 54 (1444), 1–26.CrossRefGoogle Scholar
Carr, Z. R., DeVoria, A. C. & Ringuette, M. J.2013b. Aspect ratio effects on the leading-edge circulation and forces of rotating flat-plate wings. In 51st AIAA Aerospace Sciences Meeting and Exhibit, pp. 1–22. AIAA Paper 2013-0675.Google Scholar
Carr, Z. R. & Ringuette, M. J. 2014 Flow structure of low-aspect-ratio rotating wings from dye visualization. AIAA J. 52 (5), 1081–1086.Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationship between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Delery, J. M. 1994 Aspects of vortex breakdown. Prog. Aerosp. Sci. 30, 1–59.CrossRefGoogle Scholar
DeVoria, A. C., Carr, Z. R. & Ringuette, M. J. 2014 On calculating forces from the flow field with application to experimental volume data. J. Fluid Mech. 749, 297–319.Google Scholar
DeVoria, A. C. & Ringuette, M. J. 2012 Vortex formation and saturation for low-aspect-ratio rotating flat-plate fins. Exp. Fluids 52 (2), 441–462.Google Scholar
Dudley, R. 2000 The Biomechanics of Insect Flight: Form, Function, Evolution. Princeton University Press.Google Scholar
Garmann, D. J. & Visbal, M. R. 2014 Dynamics of revolving wings for various aspect ratios. J. Fluid Mech. 748, 932–956.Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D. 2013 Three-dimensional flow structure and aerodynamic loading on a revolving wing. Phys. Fluids 25, 1–27; 034101.Google Scholar
Granlund, K., Ol, M., Bernal, L. & Kast, S.2010 Experiments on free-to-pivot hover motions of flat plates. AIAA Paper 2010-4456, pp. 1–18.Google Scholar
Granlund, K., Ol, M., Taira, K. & Jantzen, R.2013 Parameter studies on rotational and translational accelerations of flat plates. AIAA Paper 2013-0068, pp. 1–16.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013 Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams and convergence zones in turbulent flows. In Proceedings of the 1988 Summer Program: Studying Turbulence Using Numerical Simulation Databases, 2, vol. 1, pp. 193–208. Center for Turbulence Research.Google Scholar
Jardin, T., Farcy, A. & David, L. 2012 Three-dimensional effects in hovering flapping flight. J. Fluid Mech. 702, 102–125.Google Scholar
Jones, A. R. & Babinsky, H. 2011 Reynolds number effects on leading edge vortex development on a waving wing. Exp. Fluids 51, 197–210.CrossRefGoogle Scholar
Kim, D. & Gharib, M. 2010 Experimental study of three-dimensional vortex structures in translating and rotating plates. Exp. Fluids 49, 329–339.Google Scholar
Lentink, D. & Dickinson, M. H. 2009 Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212, 2705–2719.Google Scholar
Lu, Y. & Shen, G. X. 2008 Three-dimensional flow structures and evolution of the leading-edge vortices on a flapping wing. J. Expl Biol. 211, 1221–1230.Google Scholar
Lu, Y., Shen, G. X. & Lai, G. J. 2006 Dual leading-edge vortices on flapping wings. J. Expl Biol. 209, 5005–5016.Google Scholar
Lucca-Negro, O. & O’Doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27, 431–481.Google Scholar
Luo, G. & Sun, M. 2005 The effects of corrugation and wing planform on the aerodynamic force production of sweeping model insect wings. Acta Mechanica Sin. 21, 531–541.Google Scholar
Noca, F., Shiels, D. & Jeon, D. 1999 A comparison of methods for evaluating time-dependant fluid dynamic forces on bodies, using only velocity fields and their derivatives. J. Fluids Struct. 13, 551–578.CrossRefGoogle Scholar
Ozen, C. A. & Rockwell, D. 2012 Three-dimensional vortex structure on a rotating wing. J. Fluid Mech. 707, 541–550.CrossRefGoogle Scholar
Ozen, C. A. & Rockwell, D.2013 Flow structure on a rotating wing: effect of wing aspect ratio and shape. AIAA Paper 2013-0676, pp. 1–17.Google Scholar
Phillips, N. & Knowles, K. 2013 Positive and negative spanwise flow development on an insect-like rotating wing. J. Aircraft 50 (5), 1321–1332.CrossRefGoogle Scholar
Poelma, C., Dickson, W. B. & Dickinson, M. H. 2006 Time-resolved reconstruction of the full velocity field around a dynamically-scaled flapping wing. Exp. Fluids 41, 213–225.Google Scholar
Ringuette, M. J., Milano, M. & Gharib, M. 2007 Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.CrossRefGoogle Scholar
Schlueter, K., Jones, A. R., Granlund, K. & Ol, M.2013 Force coefficients of low Reynolds number rotating wings. AIAA Paper 2013-0832, pp. 1–11.Google Scholar
Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C.-K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46, 284–327.CrossRefGoogle Scholar
Shyy, W., Trizila, P., Kang, C.-K. & Aono, H. 2009 Can tip vortices enhance lift of a flapping wing? AIAA J. 47 (2), 289–293; (Aerospace Letters).Google Scholar
Sun, M. & Wu, J. 2004 Large aerodynamic forces on a sweeping wing at low Reynolds number. Acta Mechanica Sin. 20 (1), 24–31.Google Scholar
Tobalske, B. W., Warrick, D. R., Clark, C. J., Powers, D. R., Hedrick, T. L., Hyder, G. A. & Biewener, A. A. 2007 Three-dimensional kinematics of hummingbird flight. J. Expl Biol. 210, 2368–2382.Google Scholar
Wojcik, C. J. & Buchholz, J. H. J. 2014a Parameter variation and the leading-edge vortex of a rotating flat plate. AIAA J. 52 (2), 348–357.Google Scholar
Wojcik, C. J. & Buchholz, J. H. J. 2014b Vorticity transport in the leading-edge vortex on a rotating blade. J. Fluid Mech. 743, 249–261.Google Scholar
Wu, J. C. 1981 Theory for aerodynamic force and moment in viscous flows. AIAA J. 19 (4), 432–441.Google Scholar