Published online by Cambridge University Press: 23 August 2018
For the past decade, the interaction force between droplets flowing in a Hele-Shaw cell has been modelled as a dipole. In this work, we use the recently derived analytical solution of Sarig et al. (J. Fluid Mech., vol. 800, 2016, pp. 264–277) of a two-droplet system, which satisfies the no-flux condition at both droplet interfaces, and compare it to results of the dipole model, which does not satisfy the no-flux condition. Unfortunately, the recently derived solution is given in terms of infinite Fourier series, making any additional straightforward analysis difficult. We derive simple approximations for these Fourier series. We show that at large spacing the approximations for the interactions reduce to the expected dipole-like solution. We also provide a new lower limit for the velocity for the case of almost touching droplets. For the case of large spacing, the derivation is extended to arbitrary droplet numbers – including an infinite lattice. We present a new correction for the dispersion relation for the perturbations. We investigate the effect of the number of droplets in a lattice, 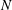 $N$, on the resulting dynamics.
$N$, on the resulting dynamics.
This work was conducted primarily at the Faculty of Mechanical Engineering, Technion–Israel Institute of Technology, Technion City 3200003, Israel.