Published online by Cambridge University Press: 27 December 2019
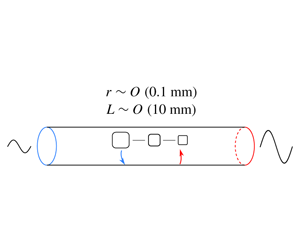
Thermoacoustic devices represent a significant future opportunity in the fields of energy generation and refrigeration. A key component of this type of device is the regenerator, where the conversion between acoustic energy and thermal energy takes place. This conversion occurs due to an externally imposed temperature gradient on the walls of the regenerator channels. Hence, this paper concerns the physics of sound waves in the proximity of such walls. It establishes a new analytical framework which clarifies the disturbance energy conservation in thermoacoustic devices. In this framework, a thermoacoustic production term is proposed to quantify the generation or consumption of disturbance energy originating from the temperature gradient. An extended disturbance energy flux term is identified to account for wave growth or decay through the regenerator. The disturbance energy balance relation states that the disturbance energy flux equals the thermoacoustic production less the viscous and thermal dissipation resulting from gradients of fluctuating velocity and temperature. The analytical framework is implemented in an axisymmetric cylindrical domain; the two-dimensional nature of this work helps to uncover that the wave always decays in the region close to the wall. A dimensional analysis is conducted to identify the controlling parameters, namely the Womersley, Helmholtz and Prandtl numbers. A parametric study of the Womersley and Helmholtz numbers is conducted to showcase the new analytical methodology; the results make it possible to optimize the geometry, wave properties and working conditions of a thermoacoustic device according to the preference of its efficiency, loss and output.