Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-10T05:36:07.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytical and experimental investigation into the effects of leading-edge radius on gust–aerofoil interaction noise

Published online by Cambridge University Press:  26 September 2017

Lorna J. Ayton Open the ORCID record for Lorna J. Ayton [Opens in a new window]  and
Paruchuri Chaitanya
Lorna J. Ayton*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Paruchuri Chaitanya
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Burgess Road, Southampton SO16 7QF, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

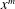This paper investigates the effects of local leading-edge geometry on unsteady aerofoil interaction noise. Analytical results are obtained by extending previous work for parabolic leading edges to leading edges of the form $x^{m}$ for 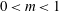$0<m<1$. Rapid distortion theory governs the interaction of an unsteady vortical perturbation with a rigid aerofoil in compressible steady mean flow that is uniform far upstream. For high-frequency gusts interacting with aerofoils of small total thickness this allows a matched asymptotic solution to be obtained. This paper mainly focusses on obtaining the analytic solution in the leading-edge inner region, which is the dominant term in determining the total far-field acoustic directivity, and contains the effects of the local leading-edge geometry. Experimental measurements for the noise generated by aerofoils with different leading-edge nose radii in uniform flow with approximate homogeneous, isotropic turbulence are also presented. Both experimental and analytic results predict that a larger nose radius generates less overall noise in low-Mach-number flow. By considering individual terms in the analytic solution, this paper is able to propose reasons behind this result.

JFM classification

Acoustics: Acoustics Acoustics: Aeroacoustics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 780 - 808
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allampalli, V., Hixon, R., Nallasamy, M. & Sawyer, S. D. 2009 High-accuracy large-step explicit Runge–Kutta (HALE-RK) schemes for computational aeroacoustics. J. Comput. Phys. 228, 3837–3850.CrossRefGoogle Scholar
Amiet, R. K. 1975 Acoustic radiation from an airfoil in a turbulent stream. J. Sound Vib. 41, 407–420.CrossRefGoogle Scholar
Ayton, L. J. 2016 An analytic solution for gust-aerofoil interaction noise including effects of geometry. IMA J. Appl. Maths 00, 1–25.Google Scholar
Ayton, L. J., Gill, J. R. & Peake, N. 2016 The Importance of the unsteady Kutta condition when modelling gust-aerofoil interaction. J. Sound Vib. 378, 28–37.CrossRefGoogle Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Chaitanya, P., Gill, J., Narayanan, S., Joseph, P., Vanderwel, C., Zhang, X. & Ganapathisubramani, B. 2015 Aerofoil geometry effects on turbulence interaction noise. In 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, AIAA Paper 2015-2830.Google Scholar
Chong, T. P., Joseph, P. F. & Davis, P. O. A. L. 2008 A parametric study of passive flow control for a short, high area ratio 90° curved diffuser. Trans. ASME J. Fluids Engng 130, 111104-12.CrossRefGoogle Scholar
Crighton, D. G. 1985 The Kutta condition in unsteady flow. Annu. Rev. Fluid Mech. 17, 411–445.CrossRefGoogle Scholar
Devenport, W. J., Staubs, J. K. & Glegg, S. A. L. 2010 Sound radiation from real airfoils in turbulence. J. Sound Vib. 329, 3470–3483.CrossRefGoogle Scholar
Gill, J., Zhang, X. & Joseph, P. 2013 Symmetric airfoil geometry effects on leading edge noise. J. Acoust. Soc. Am. 134, 2669–2680.CrossRefGoogle ScholarPubMed
Gill, J., Zhang, X. & Joseph, P. 2014 Reduced dimension modeling of leading edge turbulent interaction noise. In 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, AIAA Paper 2014-2321.Google Scholar
Glegg, S. A. L. & Devenport, W. 2009 Unsteady loading on an airfoil of arbitrary thickness. J. Sound Vib. 319, 1252–1270.CrossRefGoogle Scholar
Goldstein, M. E. 1978 Unsteady vortical and entropic distortions of potential flows round arbitrary obstacles. J. Fluid Mech. 89, 433–468.CrossRefGoogle Scholar
Grace, S. M. 2001 Unsteady blade response: the BVI model versus the gust model. In 7th AIAA/CEAS Aeroacoustics Conference, Maastricht, AIAA Paper 2001-2209.Google Scholar
Hall, A. M., Atassi, O. V. & Gilson, J. 2011 Effects of leading-edge thickness on high-speed aerofoil-turbulence interaction noise. In 17th AIAA/CEAS Aeroacoustics Conference, Portland, Oregon, AIAA Paper 2011-2861.Google Scholar
Hinze, J. O. 1959 Turbulence. McGraw-Hill.Google Scholar
Lockard, D. P. & Morris, P. J. 1998 Radiated noise from airfoils in realistic mean flows. AIAA J. 36, 907–914.CrossRefGoogle Scholar
Myers, M. R. & Kerschen, E. J. 1995 Influence of incidence angle on sound generation by airfoils interacting with high-frequency gusts. J. Fluid Mech. 292, 271–304.CrossRefGoogle Scholar
Myers, M. R. & Kerschen, E. J. 1997 Influence of camber on sound generation by airfoils interacting with high-frequency gusts. J. Fluid Mech. 353, 221–259.CrossRefGoogle Scholar
Narayanan, S., Chaitanya, P., Haeri, S., Joseph, P., Kim, J. W. & Polacsek, C. 2015 Airfoil noise reductions through leading edge serrations. Phys. Fluids 27, 025109.CrossRefGoogle Scholar
Olsen, W. & Wagner, J. 1982 Effect of thickness on airfoil surface noise. AIAA J. 20, 437–439.CrossRefGoogle Scholar
Peake, N. & Parry, A. B. 2012 Modern challenges facing turbomachinery aeroacoustics. Annu. Rev. Fluid Mech. 44, 227–248.CrossRefGoogle Scholar
Roach, P. E. 1987 The generation of nearly isotropic turbulence by mean of grid. Intl J. Heat Fluid Flow 8, 82–92.CrossRefGoogle Scholar
Sears, W. R. 1941 Some aspects of non-stationary airfoil theory and its practical applications. J. Aero. Sci. 8, 104–188.Google Scholar
Thwaites, B. 1960 Incompressible Aerodynamics: An Account of the Theory and Observation of the Steady Flow of Incompressible Fluid Past Aerofoils, Wings, and Other Bodies. Dover Publications.CrossRefGoogle Scholar
Tsai, C-T.1992 Effect of airfoil thickness on high-frequency gust interaction noise. PhD thesis, University of Arizona.Google Scholar
Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. Parabolic Press.Google Scholar