Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T11:10:19.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic model of a resistive magnetohydrodynamic shock without Hall effect

Published online by Cambridge University Press:  07 March 2018

Roland P. H. Berton Open the ORCID record for Roland P. H. Berton [Opens in a new window]
Roland P. H. Berton*
Affiliation:
ONERA, Chemin de la Hunière, BP 80100, 91123 Palaiseau CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An analytic model of a stationary hypersonic magnetohydrodynamic (MHD) shock with an externally applied magnetic field is proposed. Basically, original jump conditions at a plane oblique shock, analogous to the Rankine–Hugoniot formulae, with a moderately resistive air plasma downstream are derived. Viscous, thermal and Hall effects are neglected, but the plasma dissociation behind the shock causing a jump of isentropic exponent is also a major input of the model. Then, a shock-fitting procedure with ambient atmospheric conditions is worked out by the coupling of these MHD jumps with thermodynamic correlations and an electric conductivity model. For an application to atmospheric entry problems, the flow behind an axisymmetric blunt-body shock is modelled with a stream function satisfying these MHD jump conditions as boundary conditions. An important feature put into evidence is a similarity rule involving the hypersonic parameter 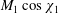$M_{1}\cos \unicode[STIX]{x1D712}_{1}$, which shows an aerodynamic correspondence between the upstream Mach number 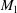$M_{1}$ and the velocity angle $\unicode[STIX]{x1D712}_{1}$. It also emerges that curvature effects become important past 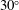$30^{\circ }$ and the assumption of a spherical shock also becomes untenable past 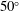$50^{\circ }$; therefore, we limit the model of shock thickness used in the MHD fitting to 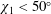$\unicode[STIX]{x1D712}_{1}<50^{\circ }$.

JFM classification

MHD and Electrohydrodynamics: Plasmas Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 273 - 322
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. D. Jr 1989 Hypersonic and High Temperature Gas Dynamics. McGraw-Hill.Google Scholar
Berton, R. P. H. 2000 Consistent determination of quasi force-free magnetic fields from observations in solar active regions. Astron. Astrophys. 356, 301–307.Google Scholar
Bisek, N. J., Boyd, I. D. & Poggie, J.2009 Numerical study of electromagnetic aerodynamic control of hypersonic vehicles. In 47th AIAA Aerospace Sciences Meeting, 5–8 January 2009, Orlando (Florida), AIAA Paper 2009-1000.Google Scholar
Bityurin, V. A. & Bocharov, A. N. 2006 Magnetohydrodynamic interaction in hypersonic air flow past a blunt body. Fluid Dyn. 41 (5), 843–856.CrossRefGoogle Scholar
Bonfiglioli, A. & Paciorri, R.2010 Hypersonic flow computations on unstructured grids: shock-capturing versus shock-fitting approach. In 40th Fluid Dynamics Conference and Exhibit, 28 June–1 July, Chicago (Illinois), AIAA Paper 2010-4449.Google Scholar
Bush, W. B. 1958 Magnetohydrodynamics-hypersonic flow past a blunt body. J. Aero. Sci. 25 (11), 685–690, 728.Google Scholar
Candler, G. V.1989 On the computation of shock shapes in nonequilibrium hypersonic flows. In 27th Aerospace Sciences Meeting, January 9–12, 1989, Reno (Nevada), AIAA Paper 1989-312.Google Scholar
Candler, G. V. & MacCormack, R. W. 1991 Computation of weakly ionized hypersonic flows in thermochemical nonequilibrium. J. Thermophys. 5 (3), 266–273.Google Scholar
Capitelli, M., Colonna, G. & D’Angola, A. 2001 Thermodynamic properties and transport coefficients of high-temperature air plasma. In Pulsed Power Plasma Science, PPPS-2001 17–22 June 2001, Las Vegas (NV, USA), vol. 1, pp. 694–697. IEEE.Google Scholar
Cavus, H.2013 On the effects of viscosity on the shock waves for a hydrodynamical case – Part I: basic mechanism. Adv. Astron. 2013, 582965, 1–6.Google Scholar
Chen, G., Zhen, H., Li, X., Su, W. & Dong, C. 2016 Numerical simulation of external MHD generator on board reentry vehicle. J. Autom. Cont. Engin. 4 (4), 273–278.CrossRefGoogle Scholar
Coackley, J. F. & Porter, R. W. 1971 Time-dependent numerical analysis of MHD blunt body problem. AIAA J. 9 (8), 1624–1626.Google Scholar
Conti, R. J. 1966 A theoretical study of non-equilibrium blunt-body flows. J. Fluid Mech. 24 (1), 65–88.CrossRefGoogle Scholar
Cowling, T. G. 1976 Magnetohydrodynamics. Adam Hilger.Google Scholar
Cristofolini, A., Borghi, C. A., Neretti, G., Passaro, A., Bacarella, D., Schettino, A. & Battista, F.2010 Experimental activities on the MHD interaction in a hypersonic air flow around a blunt body. In AIAA 41st Plasmadynamics and Lasers Conference, 28 June–1 July 2010, Chicago (Illinois), AIAA Paper 2010-4490.Google Scholar
Cristofolini, A., Borghi, C. A., Neretti, G., Passaro, A., Fantoni, G. & Paganucci, F. 2008 Magnetohydrodynamics interaction over an axisymmetric body in a hypersonic flow. J. Spacecr. Rockets 45 (3), 438–444.CrossRefGoogle Scholar
De Crombrugghe, G., Gilfind, D., Zander, F., McIntyre, T. & Morgan, R. 2014 Design of test flows to investigate binary scaling in high enthalpy CO2 –N2 mixtures. In 19th Australasian Fluid Mechanics Conference, Melbourne (Australia), 8–11 December 2014, RMIT University.Google Scholar
Dunn, M. G. & Kang, S.1973 Theoretical and experimental studies of reentry plasmas. NASA CR 2232.Google Scholar
Ericson, W. B. & Maciulaitis, A. 1964 Investigation of magnetohydrodynamic flight control. J. Spacecraft 1 (3), 283–289.Google Scholar
Evans, J. S., Schexnayder, C. J. Jr. & Huber, P. W. 1973 Boundary-layer electron profiles for entry of a blunt slender body at high altitude. NASA TN D 7332.Google Scholar
Falanga, R. A. & Sullivan, E. M.1970 An inverse-method solution for radiating, nonadiabatic, equilibrium inviscid flow over a blunt body. NASA TN D 5907.Google Scholar
Fujino, T. & Ishikawa, M.2013 Numerical simulation of MHD flow control along super orbital reentry trajectory. In 44th AIAA Plasmadynamics and Lasers Conference, 24–27 June 2013, San Diego (CA), AIAA Paper 2013-3000.Google Scholar
Gilbarg, D. & Paolucci, D. 1953 The structure of shock waves in the continuum theory of fluids. J. Rat. Mech. Anal. 2, 617–642.Google Scholar
Glass, I. I. & Hall, J. G.1959 Handbook of Supersonic Aerodynamics. Section 18. Shock Tubes. NAVORD R-1488.Google Scholar
Hall, J. G., Eschenroeder, A. Q. & Marrone, P. V. 2003 Blunt-nose inviscid airflows with coupled nonequilium processes. J. Spacecr. Rockets 40 (5), 796–809.Google Scholar
Hayes, W. D. 1957 The vorticity jump across a gasdynamic discontinuity. J. Fluid Mech. 2 (6), 595–600.Google Scholar
Hayes, W. D. & Probstein, R. F. 1959 Hypersonic Flow Theory. Academic.Google Scholar
Hida, K. 1953 An approximate study on the detached shock wave in front of a circular cylinder and a sphere. J. Phys. Soc. Japan 8 (6), 740–745.CrossRefGoogle Scholar
Huber, P. W.1958 Tables and graphs of normal-shock parameters at hypersonic Mach numbers and selected altitudes. NACA TN 4352.Google Scholar
Huber, P. W.1963 Hypersonic shock-heated flow parameters for velocities to 46 000 feet per second and altitudes to 323 000 feet. NASA TR R-163.Google Scholar
Hugoniot, H.1889 Mémoire sur la propagation du mouvement dans les corps et spécialement dans les gaz parfaits. Deuxième partie. 58ème cahier, 1–125.Google Scholar
Itakawa, Y. 2006 Cross sections for electron collisions with nitrogen molecules. J. Phys. Chem. Ref. Data 35 (1), 31–53.Google Scholar
Jarvinen, P. O.1965 On the use of magnetohydrodynamics during high speed re-entry. NASA CR-206.Google Scholar
Josyula, E. & Bailey, W. F. 2003 Governing equations for weakly ionized plasma flow fields of aerospace vehicles. J. Spacecr. Rockets 40 (6), 845–857.CrossRefGoogle Scholar
Kawamura, T. 1950 On the detached shock wave in front of a body moving at speeds greater than that of sound. Mem. Coll. Sci., Univ. Kyoto A 26 (3), 207–232.Google Scholar
Kawamura, T. 1952 On the detached shock wave in front of a body of revolution moving with supersonic speeds. J. Phys. Soc. Japan 7 (5), 486–488.Google Scholar
Kawamura, T. 1952–53 A note on the detached shock wave in front of a body. Appl. Mech. 5 (30–31), 162–165.Google Scholar
Levy, R. H. 1963 A simple MHD flow with Hall effect. AIAA J. 1 (3), 698–699.Google Scholar
Levy, R. H. & Petschek, H. E. 1963 Magnetohydrodynamically supported hypersonic shock layer. Phys. Fluids 6 (7), 946–961.CrossRefGoogle Scholar
Lighthill, M. J. 1957 Dynamics of a dissociating gas. Part I – equilibrium flow. J. Fluid Mech. 2 (1), 1–32.Google Scholar
Lykoudis, P. S. 1961 The Newtonian approximation in magnetic hypersonic stagnation point flow. J. Aerosp. Sci. 28, 541–546.Google Scholar
Maicke, B., Barber, T. & Majdalani, J.2010 Analytical methodologies for hypersonic propulsion. In 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Joint Propulsion Conferences, 25–28 July, Nashville (TN), AIAA Paper 2010-6553.Google Scholar
Maslen, S. H. 1964 Inviscid hypersonic flow past smooth symmetric bodies. AIAA J. 2 (6), 1055–1061.CrossRefGoogle Scholar
Moretti, G. 2002 Thirty-six years of shock fitting. Comput. Fluids 31 (4), 719–723.Google Scholar
Moretti, G. & Abbett, M. 1966 A time-dependent computational method for blunt body flows. AIAA J. 4 (12), 2436–2141.Google Scholar
Moretti, G. & Bleich, G. 1967 Three-dimensional flows around blunt bodies. AIAA J. 5 (9), 1557–1562.Google Scholar
Muylaert, J., Walpot, L., Ottens, H. & Cipollini, F.2007 Aerothermodynamic reentry flight experiments EXPERT. RTO-EN-AVT-130, Paper 13.Google Scholar
Nagata, Y., Satofuka, Y., Watanabe, Y., Tezuka, A., Yamada, K. & Abe, T.2013 Experimental study on the magneto-aerodynamic force deflected by magnetic field interaction in a weakly-ionized plasma flow. In 44th AIAA Plasmadynamics and Lasers Conference, 24–27 June 2013, San Diego (CA), AIAA Paper 2013-2999.Google Scholar
Noori, S., Hosseini, S. A. & Ebrahimi, M. 2009 An approximate engineering method for aerodynamic heating solution around blunt body nose. Engng Tech. 70, 893–897.Google Scholar
Oguchi, H. 1960 Blunt body viscous layer with and without a magnetic field. Phys. Fluids 3, 567–580.Google Scholar
Otsu, H., Konigorski, D. & Abe, T. 2010 Influence of Hall effect on electrodynamic heat shield system for reentry vehicles. AIAA J. 48 (10), 2177–2186.Google Scholar
Otsu, H., Matsuda, A., Abe, T. & Konigorski, D.2006 Numerical validation of the magnetic flow control for reentry vehicles. In 37th AIAA Plasmadynamics and Lasers Conference, 5–8 June 2006, San Francisco (CA), AIAA Paper 2006-3236.Google Scholar
Paolucci, S. & Paolucci, C.2016 Shock structure in hypersonic flows. XXIV ICTAM, 21–26 August 2016, Montreal (Canada).Google Scholar
Parker, E. N. 1959 Plasma dynamic determination of shock thickness in an ionized gas. Astrophys. J. 129, 217–223.CrossRefGoogle Scholar
Pepe, R., Bonfiglioli, A., D’Angola, A., Colonna, G. & Paciorri, R. 2014 Shock-fitting versus shock-capturing modeling of strong shocks in nonequilibrium plasmas. IEEE Trans. Plasma Sci. 42 (10), 2526–2527.CrossRefGoogle Scholar
Pepe, R., Bonfiglioli, A., D’Angola, A., Colonna, G. & Paciorri, R. 2015 An unstructured shock-fitting solver for hypersonic plasma flows in chemical non-equilibrium. Comput. Phys. Commun. 196, 179–193.Google Scholar
Poggie, J. & Gaitonde, D. V. 2002 Magnetic control of flow past a blunt body: numerical validation and exploration. Phys. Fluids 14 (5), 1720–1731.Google Scholar
Priest, E. 1987 Solar Magneto-Hydrodynamics Dordrecht.Google Scholar
Rankine, W. J. M. 1870 On the thermodynamic theory of waves of finite longitudinal disturbance. Proc. R. Soc. Lond. 160, 277–288.Google Scholar
Rusanov, E. E. 1976 A blunt body in a supersonic stream. Annu. Rev. Fluid Mech. 8, 377–404.Google Scholar
Saeks, R. & Murray, J.2003 Analysis of the modified Rankine Hugoniot equations. In 34th AIAA Plasmadynamics and Lasers Conference, 23–26 June 2003, Orlando (FL), AIAA Paper 2003-4180.Google Scholar
Salas, M. D. & Iollo, A. 1996 Entropy jump across an inviscid shock wave. Theor. Comput. Fluid Dyn. 8, 365–375.Google Scholar
Santos, W. F. N. 2012 Aerothermodynamic analysis of a reentry Brazilian satellite. Braz. J. Phys. 42 (5), 373–390.Google Scholar
Schexnayder, C. J. Jr., Huber, P. W. & Evans, J. S. 1971 Calculation of electron concentration for a blunt body at orbital speeds and comparison with experimental data. NASA TN D 6294.Google Scholar
Shapiro, A. 1953 The Dynamics and Thermodynamics of Compressible Fluid Flow. The Ronald Press.Google Scholar
Sharma, V. D. & Ram, R. 1971 The vorticity jump across a stationary magnetohydrodynamic discontinuity. Z. Angew. Math. Phys. 22, 1126–1134.CrossRefGoogle Scholar
Srinivasan, S., Tannehill, J. C. & Weilmuenster, K. J.1987 Simplified curve fits for the thermodynamic properties of equilibrium air. NASA RP 1181.Google Scholar
Sutherland, W. 1893 The viscosity of gases and molecular force. Phil. Mag. 5 36, 507–531.Google Scholar
Sutton, G. W. & Sherman, A. 2006 Engineering Magnetohydrodynamics. Dover.Google Scholar
Takahashi, Y., Nakasato, R. & Oshima, N. 2016 Analysis of radio frequency blackout for a blunt-body capsule in atmospheric reentry missions. Aerospace 3 (2), 3010002.Google Scholar
Tannehill, J. C. & Mugge, P. H.1974 Improved curve fits for the thermodynamic properties of equilibrium air suitable for numerical computation using time-dependent or shock-capturing methods. NASA CR 2470.Google Scholar
Tran, A. & Polk, C. 1979a Schumann resonances and electrical conductivity of the atmosphere and lower ionosphere – I. Effects of conductivity at various altitudes on resonance frequencies and attenuation. J. Atmos. Terr. Phys. 41, 1241–1248.CrossRefGoogle Scholar
Tran, A. & Polk, C. 1979b Schumann resonances and electrical conductivity of the atmosphere and lower ionosphere – II. Evaluation of conductivity profiles from experimental Schumann resonance data. J. Atmos. Terr. Phys. 41, 1249–1261.Google Scholar
Truesdell, C. 1952 On curved shocks in steady plane flow of an ideal fluid. J. Aero. Sci. 19, 826–828.CrossRefGoogle Scholar
Van Dyke, M. D. 1958 The supersonic blunt-body problem – review and extension. J. Aerosp. Sci. 25 (8), 485–496.Google Scholar
Viegas, J. R. & Peng, T. C. 1961 Electrical conductivity of ionized air in thermodynamic equilibrium. ARS J. 31, 654–657.Google Scholar
Wu, C.-S. 1960 Hypersonic viscous flow near the stagnation point in the presence of magnetic field. J. Aerosp. Sci. 27, 882–893, 950.CrossRefGoogle Scholar
Zel’dovich, Ya. B. & Raizer, Yu. P. 1967 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena, vol. 2. Academic.Google Scholar
Ziemer, R. W. & Bush, W. B. 1958 Magnetic field effects on bow shock stand-off distance. Phys. Rev. Lett. 1 (2), 58–59.Google Scholar