Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T08:04:05.316Z Has data issue: false hasContentIssue false
  • English
  • Français

An inviscid analysis of swept oblique shock reflections

Published online by Cambridge University Press:  17 March 2020

James A. S. Threadgill Open the ORCID record for James A. S. Threadgill [Opens in a new window]  and
Jesse C. Little Open the ORCID record for Jesse C. Little [Opens in a new window]
James A. S. Threadgill*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
Jesse C. Little
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

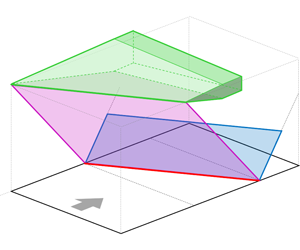
An inviscid flow model is presented to gain a basic understanding of the reflection of a swept oblique shock from a planar wall. The analytical model is constructed to describe the fundamental influence of sweep on this shock configuration, which has been commonly studied as an unswept non-dimensional shock boundary layer interaction (SBLI). Transformation of model parameters into a plane perpendicular to the sweep angle reduces the resultant flow to a two-parameter system. An equivalency between this configuration and others commonly assessed is presented with advisory notes on the definition of effective coordinate systems. Inviscid shock detachment has been associated with the onset of quasi-conical SBLI spanwise development; see (Settles & Teng, AIAA J., vol. 22 (2), 1984, pp. 194–200). Its occurrence for this SBLI configuration is determined for a range of conditions and compared to experimental observations of swept SBLIs claiming cylindrical/conical similarity scalings. Finally, influence of a zero-mass flux plane associated with typical experimental and numerical analyses is presented with an accompanying model for the shock structure. While this paper serves as a useful resource when designing swept impinging oblique SBLI studies, it also provides a vital benchmark for this complex configuration and helps to unify various SBLI configurations that are often analysed in isolation.

JFM classification

Aerodynamics: High-speed flow Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , A22
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, M. C. & Gaitonde, D. V. 2017 Unsteadiness in swept-compression-ramp shock/turbulent-boundary-layer interactions. In 55th AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Alvi, F. S. & Settles, G. S. 1992 Physical model of the swept shock wave/boundary-layer interaction flowfield. AIAA J. 30 (9), 2252–2258.CrossRefGoogle Scholar
Anderson, J. D. 2004 Modern Compressible Flow: With Historical Perspective, 3rd edn. McGraw-Hill.Google Scholar
Arora, N., Ali, M. Y. & Alvi, F. S. 2016 Flowfield of a 3-D swept shock boundary layer interaction in a Mach 2 flow. In 46th AIAA Fluid Dynamics Conference. AIAA.Google Scholar
Babaev, D. A. 1963 Numerical solution of the problem of supersonic flow past the lower surface of a delta wing. AIAA J. 1 (9), 2224–2231.CrossRefGoogle Scholar
Bachalo, W. D. 1975 Experiments on supersonic boundary-layer separation in three dimensions. Trans. ASME J. Appl. Mech. 42 (2), 289–294.CrossRefGoogle Scholar
Ben-Dor, G. 2007 Shock Wave Reflection Phenomena, 2nd edn. Springer.Google Scholar
Bruce, P. J. K. & Colliss, S. P. 2015 Review of research into shock control bumps. Shock Waves 25 (5), 451–471.CrossRefGoogle Scholar
Chapman, D. R., Kuehn, D. M. & Larson, H. K.1958 Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transition. NACA, Tech. Rep. Moffett Field, CA.Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-Frequency Unsteadiness of Shock Wave/Turbulent Boundary Layer Interactions. Annu. Rev. Fluid Mech. 46 (1), 469–492.CrossRefGoogle Scholar
Dawson-Ruiz, R. A., Pederson, C. & Little, J. C. 2015 Effects of sweep on impinging oblique shock-turbulent boundary layer interaction. In 45th AIAA Fluid Dynamics Conference. AIAA.Google Scholar
Délery, J. M. 1985 Shock wave/turbulent boundary layer interaction and its control. Prog. Aerosp. Sci. 22 (4), 209–280.CrossRefGoogle Scholar
Doehrmann, A. C., Padmanabhan, S., Threadgill, J. A. S. & Little, J. C. 2018 Effect of sweep on the mean and unsteady structures of impinging shock/boundary layer interactions. In 56th AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction research – What next? AIAA J. 39 (8), 1517–1531.CrossRefGoogle Scholar
Domel, N. D. 2016 General three-dimensional relation for oblique shocks on swept ramps. AIAA J. 54 (1), 310–319.CrossRefGoogle Scholar
Erengil, M. E. & Dolling, D. S. 1993 Effects of sweepback on unsteady separation in Mach 5 compression ramp interactions. AIAA J. 31 (2), 302–311.CrossRefGoogle Scholar
Fang, J., Yao, Y., Zheltovodov, A. A. & Lu, L. 2017 Investigation of three-dimensional shock wave/turbulent-boundary-layer interaction initiated by a single fin. AIAA J. 55 (2), 509–523.CrossRefGoogle Scholar
Fowell, L. R. 1956 Exact and Approximate Solutions for the Supersonic Delta Wing. J. Aeronaut. Sci. 23 (8), 709–720.CrossRefGoogle Scholar
Gross, A. & Fasel, H. F. 2016 Numerical investigation of shock boundary-layer interactions. In 54th AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Gross, A., Little, J. C. & Fasel, H. F. 2018 Numerical investigation of shock wave turbulent boundary layer interactions. In 2018 AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Hainsworth, J., Dawson-Ruiz, R. A. & Little, J. C. 2014 Experimental study of unswept and swept oblique shock- turbulent boundary layer interactions. In 32nd AIAA Applied Aerodynamics Conference. AIAA.Google Scholar
Hayes, W. D. & Probstein, R. F. 1959 Hypersonic Flow Theory, vol. 5. Academic Press.CrossRefGoogle Scholar
Holden, M. S.1984 Experimental studies of quasi-two-dimensional and three-dimensional viscous interaction regions induced by skewed-shock and swept-shock boundary layer interactions. Tech. Rep. CALSPAN-7018-A-2. Arvin/Calspan Advanced Technology Center, Buffalo, NY.CrossRefGoogle Scholar
Klunker, E. B., South, Jerry C Jr & Davis, R. M.1971 Calculation of nonlinear conical flows by the method of lines. Tech. Rep. TR R-374. NASA Langley.Google Scholar
Lu, F. K. 1993 Quasiconical free interaction between a swept shock and a turbulent boundary layer. AIAA J. 31 (4), 686–692.CrossRefGoogle Scholar
Lu, F. K. & Settles, G. S. 1990 Inception length to a fully developed, fin-generated, shock-wave, boundary-layer interaction. AIAA J. 29 (5), 758–762.CrossRefGoogle Scholar
Lu, F. K., Settles, G. S. & Horstman, C. C. 1990 Mach number effects on conical surface features of swept shock-wave/boundary-layer interactions. AIAA J. 28 (1), 91–97.CrossRefGoogle Scholar
Messiter, A. F. 1963 Lift of slender delta wings according to newtonian theory. AIAA J. 1 (4), 794–802.CrossRefGoogle Scholar
Morgan, B. E., Duraisamy, K., Nguyen, N., Kawai, S. & Lele, S. K. 2013 Flow physics and RANS modelling of oblique shock/turbulent boundary layer interaction. J. Fluid Mech. 729 (2013), 231–284.CrossRefGoogle Scholar
Padmanabhan, S., Castro Maldonado, J., Threadgill, J. A. S. & Little, J. C. 2019 Experimental study of swept impinging oblique shock boundary layer interaction. In AIAA Scitech 2019 Forum. AIAA.Google Scholar
Roe, P. L.1970 A simple treatment of the attached shock layer on a delta wing. Tech. Rep. TR 70246. Royal Aircraft Establishment.Google Scholar
Roe, P. L.1972 A result concerning the supersonic flow below a plane delta wing. Tech. Rep. CP No. 1228. Royal Aircraft Establishment.Google Scholar
Rosen, R., Roshko, A. & Pavish, D. L. 1980 A two-layer calculation for the initial interaction region of an unseparated supersonic turbulent boundary layer with a ramp. In 18th Aerospace Sciences Meeting. AIAA.Google Scholar
Sansica, A., Sandham, N. D. & Hu, Z. 2016 Instability and low-frequency unsteadiness in a shock-induced laminar separation bubble. J. Fluid Mech. 798, 5–26.CrossRefGoogle Scholar
Settles, G. S. & Bogdonoff, S. M. 1982 Scaling of two- and three-dimensional shock/turbulent boundary-layer interactions at compression corners. AIAA J. 20 (6), 782–789.CrossRefGoogle Scholar
Settles, G. S. & Dolling, D. S. 1992 Swept shock wave/boundary-layer interactions. In Tactical Missile Aerodynamics: General Topics (ed. Hemsch, M. J.), Progress in Astronautics & Aeronautics, vol. 141, chap. 12, pp. 505–574. AIAA.Google Scholar
Settles, G. S., Horstman, C. C. & McKenzie, T. M. 1986 Experimental and computational study of a swept compression corner interaction flowfield. AIAA J. 24 (5), 744–752.CrossRefGoogle Scholar
Settles, G. S. & Kimmel, R. L. 1986 Similarity of quasiconical shock wave/turbulent boundary-layer interactions. AIAA J. 24 (1), 47–53.CrossRefGoogle Scholar
Settles, G. S. & Lu, F. K. 1985 Conical similarity of shock/boundary-layer interactions generated by swept and unswept fins. AIAA J. 23 (7), 1021–1027.CrossRefGoogle Scholar
Settles, G. S., Perkins, J. J. & Bogdonoff, S. M. 1980 Investigation of three-dimensional shock/boundary-layer interactions at swept compression corners. AIAA J. 18 (7), 779–785.CrossRefGoogle Scholar
Settles, G. S. & Teng, H.-ying 1984 Cylindrical and conical flow regimes of three-dimensional shock/boundary-layer interactions. AIAA J. 22 (2), 194–200.CrossRefGoogle Scholar
Sivasubramanian, J. & Fasel, H. F. 2016 Numerical investigation of shockwave boundary layer interactions in supersonic flows. In 54th AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Souverein, L. J., Bakker, P. G. & Dupont, P. 2013 A scaling analysis for turbulent shock-wave/boundary-layer interactions. J. Fluid Mech. 714, 505–535.CrossRefGoogle Scholar
Squire, L. C. 1968 Calculated pressure distributions and shock shapes on conical wings with attached shock waves. Aeronaut. Q. 19 (1), 31–50.CrossRefGoogle Scholar
Threadgill, J. A. S., Stab, I., Doehrmann, A. C. & Little, J. C. 2017 Three-dimensional flow features of swept impinging oblique shock/boundary-layer interactions. In 55th AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Vanstone, L., Bosco, A., Saleh, Y., Akella, M. R., Clemens, N. T. & Gogineni, S. P. 2019 Closed-loop control of unstart in a Mach 1.8 isolator. In AIAA Scitech 2019 Forum. AIAA.Google Scholar
Vanstone, L. & Clemens, N. T. 2018 POD analysis of unsteadiness mechanisms within a swept compression-ramp shock-wave boundary-layer interaction at Mach 2. In 2018 AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Vanstone, L., Hashemi, K. E., Lingren, J., Akella, M. R., Clemens, N. T., Donbar, J. M. & Gogineni, S. P. 2017a Closed-loop control of isolator shock trains in a Mach 2.2 direct-connect scramjet. In 55th AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Vanstone, L., Saleem, M., Seckin, S. & Clemens, N. T. 2017b Role of boundary-layer on unsteadiness on a Mach 2 swept-ramp shock/boundary-layer interaction using 50 kHz PIV. In 55th AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Voskresenskii, G. P. 1968 Numerical solution of the problem of a supersonic gas flow past an arbitrary surface of a delta wing in the compression region. Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza 4, 134–142.Google Scholar
Woods, B. A. 1970 Hypersonic flow with attached shock waves over delta wings. Aeronaut. Q. 21 (4), 379–399.CrossRefGoogle Scholar