Published online by Cambridge University Press: 29 September 2017
An emerging long obstacle placed in a boundary layer developing under a free surface generates a complex horseshoe vortex (HSV) system, which is composed of a set of vortices exhibiting a rich variety of dynamics. The present experimental study examines such flow structure and characterizes precisely, using particle image velocimetry (PIV) measurements, the evolution of the HSV geometrical and dynamical properties over a wide range of dimensionless parameters (Reynolds number
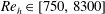 $Re_{h}\in [750,8300]$
, boundary layer development ratio
$Re_{h}\in [750,8300]$
, boundary layer development ratio
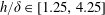 $h/\unicode[STIX]{x1D6FF}\in [1.25,4.25]$
and obstacle aspect ratio
$h/\unicode[STIX]{x1D6FF}\in [1.25,4.25]$
and obstacle aspect ratio
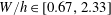 $W/h\in [0.67,2.33]$
). The dynamical study of the HSV is based on the categorization of the motions of HSV vortices that result in an enhanced specific bi-dimensional typology, separating a coherent (due to vortex–vortex interactions) and an irregular evolution (due to the appearance of small-scale instabilities). This precise categorization is made possible thanks to the use of vortex tracking methods applied to PIV measurements; a semi-empirical model for the motion of the HSV vortices is then proposed to highlight some important mechanisms of the HSV dynamics, such as (i) the influence of the surrounding vortices on vortex motion and (ii) the presence of a phase shift between the motion of all vortices. Finally, the study of the HSV’s geometrical properties (vortex position and characteristic lengths and frequencies) evolution with the flow parameters shows that strong dependencies exist between the streamwise extension of the HSV and the obstacle width, and between the HSV vortex number and its elongation. Comparison of these data with prior studies for immersed obstacles reveals that emerging obstacles lead to greater adverse pressure gradients and down-flows in front of the obstacle. This implies a precocious separation of the boundary layer, leading to a larger HSV streamwise extension, and a lower vertical extension of the HSV, leading to smaller HSV vortices.
$W/h\in [0.67,2.33]$
). The dynamical study of the HSV is based on the categorization of the motions of HSV vortices that result in an enhanced specific bi-dimensional typology, separating a coherent (due to vortex–vortex interactions) and an irregular evolution (due to the appearance of small-scale instabilities). This precise categorization is made possible thanks to the use of vortex tracking methods applied to PIV measurements; a semi-empirical model for the motion of the HSV vortices is then proposed to highlight some important mechanisms of the HSV dynamics, such as (i) the influence of the surrounding vortices on vortex motion and (ii) the presence of a phase shift between the motion of all vortices. Finally, the study of the HSV’s geometrical properties (vortex position and characteristic lengths and frequencies) evolution with the flow parameters shows that strong dependencies exist between the streamwise extension of the HSV and the obstacle width, and between the HSV vortex number and its elongation. Comparison of these data with prior studies for immersed obstacles reveals that emerging obstacles lead to greater adverse pressure gradients and down-flows in front of the obstacle. This implies a precocious separation of the boundary layer, leading to a larger HSV streamwise extension, and a lower vertical extension of the HSV, leading to smaller HSV vortices.