Article contents
An exact representation of the nonlinear triad interaction terms in spectral space
Published online by Cambridge University Press: 28 April 2014
Abstract
Spectral analysis of the Navier–Stokes equations requires treatment of the convolution of pairs of Fourier transforms 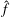 $\hat{f}$ and
$\hat{f}$ and 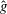 $\hat{g}$. An exact, tractable representation of the nonlinear terms in spectral space is introduced, and relies on the definition and manipulation of a combination matrix. A spectral energy equation is derived where the nonlinear triad interactions are expressed using the combination matrix. The formulation is applied to the problem of homogeneous, isotropic turbulence. By finding the solution in an appropriate canonical basis, the energy spectrum in the inertial range
$\hat{g}$. An exact, tractable representation of the nonlinear terms in spectral space is introduced, and relies on the definition and manipulation of a combination matrix. A spectral energy equation is derived where the nonlinear triad interactions are expressed using the combination matrix. The formulation is applied to the problem of homogeneous, isotropic turbulence. By finding the solution in an appropriate canonical basis, the energy spectrum in the inertial range 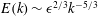 $E(k)\sim \epsilon ^{2/3}k^{-5/3}$ is derived from the Navier–Stokes equations without invoking dimensional scaling arguments.
$E(k)\sim \epsilon ^{2/3}k^{-5/3}$ is derived from the Navier–Stokes equations without invoking dimensional scaling arguments.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 10
- Cited by


