Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T08:56:34.320Z Has data issue: false hasContentIssue false
  • English
  • Français

An algorithm for solving the Navier–Stokes equations with shear-periodic boundary conditions and its application to homogeneously sheared turbulence

Published online by Cambridge University Press:  08 November 2017

M. Houssem Kasbaoui Open the ORCID record for M. Houssem Kasbaoui [Opens in a new window] ,
Ravi G. Patel ,
Donald L. Koch Open the ORCID record for Donald L. Koch [Opens in a new window]  and
Olivier Desjardins
M. Houssem Kasbaoui
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Ravi G. Patel
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Donald L. Koch
Affiliation:
Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
Olivier Desjardins
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Simulations of homogeneously sheared turbulence (HST) are conducted until a universal self-similar state is established at the long non-dimensional time 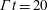$\unicode[STIX]{x1D6E4}t=20$, where 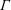$\unicode[STIX]{x1D6E4}$ is the shear rate. The simulations are enabled by a new robust and discretely conservative algorithm. The method solves the governing equations in physical space using the so-called shear-periodic boundary conditions. Convection by the mean homogeneous shear flow is treated implicitly in a split step approach. An iterative Crank–Nicolson time integrator is chosen for robustness and stability. The numerical strategy captures without distortion the Kelvin modes, rotating waves that are fundamental to homogeneously sheared flows and are at the core of rapid distortion theory. Three direct numerical simulations of HST with the initial Taylor scale Reynolds number 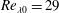$Re_{\unicode[STIX]{x1D706}0}=29$ and shear numbers of 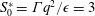$S_{0}^{\ast }=\unicode[STIX]{x1D6E4}q^{2}/\unicode[STIX]{x1D716}=3$, 15 and 27 are performed on a 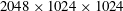$2048\times 1024\times 1024$ grid. Here, $\unicode[STIX]{x1D716}$ is the dissipation rate and 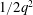$1/2q^{2}$ is the turbulent kinetic energy. The long integration time considered allows the establishment of a self-similar state observed in experiments but often absent from simulations conducted over shorter times. The asymptotic state appears to be universal with a long time production to dissipation rate 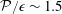${\mathcal{P}}/\unicode[STIX]{x1D716}\sim 1.5$ and shear number 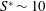$S^{\ast }\sim 10$ in agreement with experiments. While the small scales exhibit strong anisotropy increasing with initial shear number, the skewness of the transverse velocity derivative decreases with increasing Reynolds number.

JFM classification

Mathematical Foundations: Computational methods Turbulent Flows: Homogeneous turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 687 - 716
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.Google Scholar
Akselvoll, K.1995. Large eddy simulation of turbulent confined coannular jets and turbulent flow over a backward facing step. PhD thesis, Stanford University, Stanford, CA.Google Scholar
Baron, F.1982. Macro-simulation tridimensionnelle d’ecoulements turbulents cisailles. PhD thesis, google-Books-ID: 78yrtgAACAAJ.Google Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414 (23), 43–164.Google Scholar
Boris, J., Luca, B., Gaetano, I. & Carlo Massimo, C. 2004 Anisotropic fluctuations in turbulent shear flows. Phys. Fluids 16 (11), 4135–4142.Google Scholar
Brucker, K. A., Isaza, J. C., Vaithianathan, T. & Collins, L. R. 2007 Efficient algorithm for simulating homogeneous turbulent shear flow without remeshing. J. Comput. Phys. 225 (1), 20–32.Google Scholar
Casciola, C. M., Gualtieri, P., Jacob, B. & Piva, R. 2005 Scaling properties in the production range of shear dominated flows. Phys. Rev. Lett. 95 (2), 024503.Google Scholar
Choi, H. & Moin, P. 1994 Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys. 113 (1), 1–4.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Maths Comput. 22 (104), 745–762.Google Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696, 434–467.Google Scholar
Desjardins, O., Blanquart, G., Balarac, G. & Pitsch, H. 2008 High order conservative finite difference scheme for variable density low Mach number turbulent flows. J. Comput. Phys. 227 (15), 7125–7159.Google Scholar
Dukowicz, J. K & Dvinsky, A. S. 1992 Approximate factorization as a high order splitting for the implicit incompressible flow equations. J. Comput. Phys. 102 (2), 336–347.Google Scholar
Ferchichi, M. & Tavoularis, S. 2000 Reynolds number effects on the fine structure of uniformly sheared turbulence. Phys. Fluids 12 (11), 2942–2953.Google Scholar
Garg, S. & Warhaft, Z. 1998 On the small scale structure of simple shear flow. Phys. Fluids 10 (3), 662–673.Google Scholar
George, W. K. & Gibson, M. M. 1992 The self-preservation of homogeneous shear flow turbulence. Exp. Fluids 13 (4), 229–238.Google Scholar
Gerz, T., Schumann, U. & Elghobashi, S. E. 1989 Direct numerical simulation of stratified homogeneous turbulent shear flows. J. Fluid Mech. 200, 563–594.Google Scholar
Goldreich, P. & Tremaine, S. 1978 The excitation and evolution of density waves. Astrophys. J. 222, 850–858.Google Scholar
Gresho, P. M. 1990 On the theory of semi-implicit projection methods for viscous incompressible flow and its implementation via a finite element method that also introduces a nearly consistent mass matrix. Part 1: theory. Intl J. Numer. Meth. Fluids 11 (5), 587–620.Google Scholar
Gualtieri, P., Casciola, C. M., Benzi, R., Amati, G. & Piva, R. 2002 Scaling laws and intermittency in homogeneous shear flow. Phys. Fluids 14 (2), 583–596.CrossRefGoogle Scholar
Gualtieri, P., Casciola, C. M., Benzi, R. & Piva, R. 2007a Preservation of statistical properties in large-eddy simulation of shear turbulence. J. Fluid Mech. 592, 471–494.Google Scholar
Gualtieri, P., Casciola, C. M., Jacob, B. & Piva, R. 2007b The residual anisotropy at small scales in high shear turbulence. Phys. Fluids 19 (10), 101704.Google Scholar
Holt, S. E., Koseff, J. R. & Ferziger, J. H. 1992 A numerical study of the evolution and structure of homogeneous stably stratified sheared turbulence. J. Fluid Mech. 237, 499–539.Google Scholar
Isaza, J. C. & Collins, L. R. 2009 On the asymptotic behaviour of large-scale turbulence in homogeneous shear flow. J. Fluid Mech. 637, 213–239.Google Scholar
Isaza, J. C. & Collins, L. R. 2011 Effect of the shear parameter on velocity-gradient statistics in homogeneous turbulent shear flow. J. Fluid Mech. 678, 14–40.Google Scholar
Isaza, J. C., Warhaft, Z., Collins, L. R. & Research, International Collaboration for Turbulence 2009 Experimental investigation of the large-scale velocity statistics in homogeneous turbulent shear flow. Phys. Fluids 21 (6), 065105.Google Scholar
Ishihara, T., Yoshida, K. & Kaneda, Y. 2002 Anisotropic velocity correlation spectrum at small scales in a homogeneous turbulent shear flow. Phys. Rev. Lett. 88 (15), 154501.Google Scholar
Jacobitz, F. G., Liechtenstein, L., Schneider, K. & Farge, M. 2008 On the structure and dynamics of sheared and rotating turbulence: direct numerical simulation and wavelet-based coherent vortex extraction. Phys. Fluids 20 (4), 045103.Google Scholar
Jacobitz, F. G., Schneider, K., Bos, W. J. T. & Farge, M. 2010 On the structure and dynamics of sheared and rotating turbulence: anisotropy properties and geometrical scale-dependent statistics. Phys. Fluids 22 (8), 085101.Google Scholar
Jacobitz, F. G., Schneider, K., Bos, W. J. T. & Farge, M. 2016 Structure of sheared and rotating turbulence: multiscale statistics of Lagrangian and Eulerian accelerations and passive scalar dynamics. Phys. Rev. E 93 (1), 013113.Google Scholar
Johnson, B. M. & Gammie, C. F. 2005 Linear theory of thin, radially stratified disks. Astrophys. J. 626 (2), 978–990.Google Scholar
Kaltenbach, H.-J., Gerz, T. & Schumann, U. 1994 Large-eddy simulation of homogeneous turbulence and diffusion in stably stratified shear flow. J. Fluid Mech. 280 (1), 1–40.Google Scholar
Kasbaoui, M. H., Koch, D. L., Subramanian, G. & Desjardins, O. 2015 Preferential concentration driven instability of sheared gassolid suspensions. J. Fluid Mech. 770, 85–123.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59 (2), 308–323.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.Google Scholar
Maxey, M. R. 1982 Distortion of turbulence in flows with parallel streamlines. J. Fluid Mech. 124, 261–282.Google Scholar
Moffatt, H. K.1965 The interaction of turbulence with Rapid Uniform Shear. SUDAER Report 242, Stanford University.Google Scholar
Orszag, S. A., Israeli, M. & Deville, M. O. 1986 Boundary conditions for incompressible flows. J. Sci. Comput. 1 (1), 75–111.Google Scholar
Pierce, C. D.2001. Progress-variable approach for large-eddy simulation of turbulent combustion. PhD thesis, Stanford University, Stanford, CA.Google Scholar
Pope, S. B. 2001 Turbulent flows. Meas. Sci. Technol. 12 (11), 2020.Google Scholar
Pumir, A. 1996 Turbulence in homogeneous shear flows. Phys. Fluids 8 (11), 3112–3127.Google Scholar
Pumir, A. & Shraiman, B. I. 1995 Persistent small scale anisotropy in homogeneous shear flows. Phys. Rev. Lett. 75 (17), 3114–3117.Google Scholar
Rogallo, R. S. 1981 Numerical experiments in homogeneous turbulence. NASA STI/Recon Tech. Rep. N 81, 31508.Google Scholar
Rogers, M. M.1986. The structure and modeling of the hydrodynamic and passive scalar fields in homogeneous turbulent shear flow. PhD Stanford University, United States–California.Google Scholar
Rogers, M. M. 1991 The structure of a passive scalar field with a uniform mean gradient in rapidly sheared homogeneous turbulent flow. Phys. Fluids A 3 (1), 144–154.Google Scholar
Rogers, M. M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.Google Scholar
Rohr, J. J., Itsweire, E. C., Helland, K. N. & Atta, C. W. V. 1988 An investigation of the growth of turbulence in a uniform-mean-shear flow. J. Fluid Mech. 187, 1–33.Google Scholar
Salhi, A., Jacobitz, F. G., Schneider, K. & Cambon, C. 2014 Nonlinear dynamics and anisotropic structure of rotating sheared turbulence. Phys. Rev. E 89 (1), 013020.Google ScholarPubMed
Schmid, P. J. & Kytomaa, H. K. 1994 Transient and asymptotic stability of granular shear flow. J. Fluid Mech. 264, 255–275.Google Scholar
Schumacher, J. R. G. 2001 Derivative moments in stationary homogeneous shear turbulence. J. Fluid Mech. 441, 109–118.Google Scholar
Schumacher, J. R. G. 2004 Relation between shear parameter and Reynolds number in statistically stationary turbulent shear flows. Phys. Fluids 16 (8), 3094–3102.Google Scholar
Schumacher, J. & Eckhardt, B. 2000 On statistically stationary homogeneous shear turbulence. Europhys. Lett. 52 (6), 627.Google Scholar
Schumann, U. 1985 Algorithms for direct numerical simulation of shear-periodic turbulence. In Ninth International Conference on Numerical Methods in Fluid Dynamics (ed. Soubbaramayer & Boujot, J. P.), Lecture Notes in Physics, vol. 218, pp. 492–496. Springer.Google Scholar
Schumann, U. 1996 Direct and large eddy simulations of stratified homogeneous shear flows. Dyn. Atmos. Oceans 23, 81–98.Google Scholar
Schumann, U., Elghobashi, S. E. & Gerz, T. 1986 Direct simulation of stably stratified turbulent homogeneous shear flows. In Direct and Large Eddy Simulation of Turbulence (ed. Schumann, U. & Friedrich, R.), pp. 245–264. Vieweg+Teubner Verlag.Google Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number (R1000) turbulent shear flow. Phys. Fluids 12 (11), 2976–2989.Google Scholar
Shotorban, B. & Balachandar, S. 2006 Particle concentration in homogeneous shear turbulence simulated via Lagrangian and equilibrium Eulerian approaches. Phys. Fluids 18 (6), 065105.Google Scholar
Sukheswalla, P., Vaithianathan, T. & Collins, L. R. 2013 Simulation of homogeneous turbulent shear flows at higher Reynolds numbers: numerical challenges and a remedy. J. Turbul. 14 (5), 60–97.Google Scholar
Tavoularis, S. 1985 Asymptotic laws for transversely homogeneous turbulent shear flows. Phys. Fluids 28 (3), 999–1001.Google Scholar
Tavoularis, S. & Corrsin, S. 1981 Experiments in nearly homogenous turbulent shear flow with a uniform mean temperature gradient. Part 1. J. Fluid Mech. 104, 311–347.Google Scholar
Tavoularis, S. & Karnik, U. 1989 Further experiments on the evolution of turbulent stresses and scales in uniformly sheared turbulence. J. Fluid Mech. 204, 457–478.Google Scholar
Temam, R. 1968 Une méthode d’approximation de la solution des équations de Navier–Stokes. Bull. Soc. Maths France 96, 115–152.Google Scholar
Teukolsky, S. A. 2000 Stability of the iterated Crank–Nicholson method in numerical relativity. Phys. Rev. D 61 (8), 087501.Google Scholar
Thomson, W. 1887 XXXIV Stability of motion (continued from the May, June, and August numbers). Broad river flowing down an inclined plane bed. Phil. Mag. 24 (148), 272–278.Google Scholar
Townsend, A. A. 1970 Entrainment and the structure of turbulent flow. J. Fluid Mech. 41 (1), 13–46.Google Scholar
Wall, C., Pierce, C. D. & Moin, P. 2002 A semi-implicit method for resolution of acoustic waves in low Mach number flows. J. Comput. Phys. 181 (2), 545–563.Google Scholar