Published online by Cambridge University Press: 23 December 2014
Air-assisted primary atomization is investigated in a configuration where liquid is injected in a turbulent gaseous jet flow both within as well as outside of the potential core. Cases are studied where the injection point is moved within the flow to maintain a range of constant gaseous mean velocities but changing local fluctuating velocity root-mean-square (r.m.s.) levels. Over a range of mean conditions, this allows for a systematic understanding of both the effects of gas-phase turbulence and mean shear on primary break-up independently. Extensive data is obtained and analysed from laser Doppler anemometry/phase Doppler anemometry, high-speed microscopic backlit imaging and advanced image processing. It is found that the ratio of the turbulent Weber number 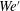 $\mathit{We}^{\prime }$ to the mean Weber number
$\mathit{We}^{\prime }$ to the mean Weber number 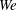 $\mathit{We}$ is a relevant parameter as is the turbulence intensity. The primary break-up length is found to be heavily influenced not only by the mean velocity, but also by the turbulence level and the mass fuel to air ratio. Above a particular threshold intensity level the break-up time changes in proportion to the change in the integral time scale of the flow. In addition, it is found that regardless of diameter and turbulent flow conditions at the liquid jet, the final size of ligaments converges to a value which is of the order of the measured primary instability wavelength (
$\mathit{We}$ is a relevant parameter as is the turbulence intensity. The primary break-up length is found to be heavily influenced not only by the mean velocity, but also by the turbulence level and the mass fuel to air ratio. Above a particular threshold intensity level the break-up time changes in proportion to the change in the integral time scale of the flow. In addition, it is found that regardless of diameter and turbulent flow conditions at the liquid jet, the final size of ligaments converges to a value which is of the order of the measured primary instability wavelength (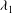 ${\it\lambda}_{1}$). In contrast, cases of different turbulence intensity show the mean of droplet sizes diverging as the spray is advected downstream and this is because droplets are generated from ligaments, the latter of which are subjected both to Rayleigh–Taylor instabilities and turbulent fluctuations. This contribution, for the first time, examines the theoretical applicability of the Rayleigh–Taylor instability in flows where the turbulence is substantial with respect to the mean flow. It is shown that for high turbulence intensities a full theoretical reconstruction of the measured final droplet size distribution is possible from a probability density function of model Rayleigh–Taylor wavelengths (
${\it\lambda}_{1}$). In contrast, cases of different turbulence intensity show the mean of droplet sizes diverging as the spray is advected downstream and this is because droplets are generated from ligaments, the latter of which are subjected both to Rayleigh–Taylor instabilities and turbulent fluctuations. This contribution, for the first time, examines the theoretical applicability of the Rayleigh–Taylor instability in flows where the turbulence is substantial with respect to the mean flow. It is shown that for high turbulence intensities a full theoretical reconstruction of the measured final droplet size distribution is possible from a probability density function of model Rayleigh–Taylor wavelengths (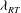 ${\it\lambda}_{RT}$). In agreement with the literature (Varga et al. J. Fluid Mech., vol. 497, 2003, pp. 405–434), mean droplet sizes are found to be equal to a mean theoretical Rayleigh–Taylor wavelength normalized by a particular constant value. This, however, is only true for local turbulence intensities less than
${\it\lambda}_{RT}$). In agreement with the literature (Varga et al. J. Fluid Mech., vol. 497, 2003, pp. 405–434), mean droplet sizes are found to be equal to a mean theoretical Rayleigh–Taylor wavelength normalized by a particular constant value. This, however, is only true for local turbulence intensities less than 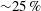 ${\sim}25\,\%$, or for ratios of the turbulent Weber number to mean Weber number (
${\sim}25\,\%$, or for ratios of the turbulent Weber number to mean Weber number (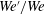 $\mathit{We}^{\prime }/\mathit{We}$) of less than
$\mathit{We}^{\prime }/\mathit{We}$) of less than 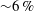 ${\sim}6\,\%$. Above this, the normalization value is no longer constant, but increases with
${\sim}6\,\%$. Above this, the normalization value is no longer constant, but increases with 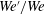 $\mathit{We}^{\prime }/\mathit{We}$. Finally, the instability wavelengths can be used as part of an approximation that estimates the total number of objects formed after break-up, where the object number is found to be dictated by a balance of both mean flow conditions and local turbulence.
$\mathit{We}^{\prime }/\mathit{We}$. Finally, the instability wavelengths can be used as part of an approximation that estimates the total number of objects formed after break-up, where the object number is found to be dictated by a balance of both mean flow conditions and local turbulence.