Published online by Cambridge University Press: 18 May 2022
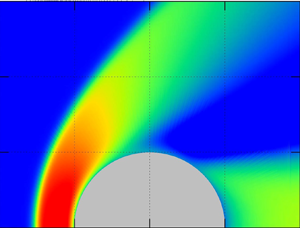
Aerothermodynamic characteristics of a sphere such as drag and energy transfer coefficients are calculated for Mach numbers varying from 1 to 10 over a wide range of the gas rarefaction degree spanning the free molecular, transitional and near hydrodynamic flow regimes. The effects of major factors determining the gas flow are studied using the direct simulation Monte Carlo method. To reveal the effect of gas species, the simulations are performed based on ab initio interatomic potentials for helium, neon, argon and krypton, as well as based on the hard sphere model. The impact of the accommodation coefficients is evaluated by applying the Cercignani–Lampis model of gas–surface interaction. The calculations are carried out for several values of the free stream and sphere temperatures. It is found that the effects of gas species on the drag and energy transfer coefficients are approximately 3 % and 6 %, respectively. The accommodation coefficients in the Cercignani–Lampis model strongly affect all aerothermodynamic characteristics. The drag and energy transfer coefficients calculated for different accommodation coefficients vary within 30 % and 200 %, respectively. It is found that the variation of the tangential momentum and normal energy accommodation coefficients can induce an increase of the drag coefficient compared to the case of diffuse gas–surface interaction. In hypersonic flows, the drag coefficient varies within 30 % when the sphere temperature varies from the free stream temperature to the stagnation temperature. The drag and energy transfer coefficients are found to be non-monotonic functions of the free stream temperature.