Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yuan, Yuan
Zhou, Kaiwen
Zhou, Wenwu
Wen, Xin
and
Liu, Yingzheng
2021.
Flow prediction using dynamic mode decomposition with time-delay embedding based on local measurement.
Physics of Fluids,
Vol. 33,
Issue. 9,
Dotto, A.
Lengani, D.
Simoni, D.
and
Tacchella, A.
2021.
Dynamic mode decomposition and Koopman spectral analysis of boundary layer separation-induced transition.
Physics of Fluids,
Vol. 33,
Issue. 10,
Sashittal, Palash
and
Bodony, Daniel J.
2021.
Data-driven sensor placement for fluid flows.
Theoretical and Computational Fluid Dynamics,
Vol. 35,
Issue. 5,
p.
709.
Zhang, Wei
and
Wei, Mingjun
2021.
Generalized eigenvalue approach for dynamic mode decomposition.
AIP Advances,
Vol. 11,
Issue. 12,
Sashittal, Palash
and
Bodony, Daniel J.
2021.
Data-Driven Sensor Placement for Fluid Flows.
Otto, Samuel E.
and
Rowley, Clarence W.
2021.
Koopman Operators for Estimation and Control of Dynamical Systems.
Annual Review of Control, Robotics, and Autonomous Systems,
Vol. 4,
Issue. 1,
p.
59.
Kou, Jiaqing
and
Zhang, Weiwei
2021.
Data-driven modeling for unsteady aerodynamics and aeroelasticity.
Progress in Aerospace Sciences,
Vol. 125,
Issue. ,
p.
100725.
Asztalos, Katherine J.
Dawson, Scott T. M.
and
Williams, David R.
2021.
Modeling the Flow State Sensitivity of Actuation Response on a Stalled Airfoil.
AIAA Journal,
p.
1.
Faiella, Matthew
Grant Jeon Macmillan, Corwin
Whitehead, Jared P
and
Pan, Zhao
2021.
Error propagation dynamics of velocimetry-based pressure field calculations (2): on the error profile.
Measurement Science and Technology,
Vol. 32,
Issue. 8,
p.
084005.
Susuki, Yoshihiko
Shimomura, Takahiro
Ota, Yutaka
and
Ishigame, Atsushi
2022.
Online Koopman Mode Decomposition for Power System Synchrophasor Data.
IFAC-PapersOnLine,
Vol. 55,
Issue. 9,
p.
54.
Sashidhar, Diya
and
Kutz, J. Nathan
2022.
Bagging, optimized dynamic mode decomposition for robust, stable forecasting with spatial and temporal uncertainty quantification.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2229,
Wu, Wen
Meneveau, Charles
Mittal, Rajat
Padovan, Alberto
Rowley, Clarence W.
and
Cattafesta, Louis
2022.
Response of a turbulent separation bubble to zero-net-mass-flux jet perturbations.
Physical Review Fluids,
Vol. 7,
Issue. 8,
Inoba, Ryoma
Uchida, Kazuki
Iwasaki, Yuto
Nagata, Takayuki
Ozawa, Yuta
Saito, Yuji
Nonomura, Taku
and
Asai, Keisuke
2022.
Optimization of sparse sensor placement for estimation of wind direction and surface pressure distribution using time-averaged pressure-sensitive paint data on automobile model.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 227,
Issue. ,
p.
105043.
Sinclair, Owen
Turner, James
Nicholls, Chris
Tang, Brian
and
Bacic, Marko
2022.
Identification and Closed-Loop Control of a Backwards Facing Step by Opposite Side Acoustic Excitation.
Heide, Alexander L.
Asztalos, Katherine J.
Dawson, Scott T.
and
Hemati, Maziar
2022.
A low-order nonlinear model of a stalled airfoil from data: Exploiting sparse regression with physical constraints.
Zheng, Changdong
Xie, Fangfang
Ji, Tingwei
Zhang, Xinshuai
Lu, Yufeng
Zhou, Hongjie
and
Zheng, Yao
2022.
Data-efficient deep reinforcement learning with expert demonstration for active flow control.
Physics of Fluids,
Vol. 34,
Issue. 11,
Xu, Xianzhang
and
Lagor, Francis D.
2023.
Simplified Iterative Maneuver Optimization in a Transverse Gust Encounter.
Unnikrishnan, S.
2023.
Recent advances in feature extraction techniques for high-speed flowfields.
Progress in Aerospace Sciences,
Vol. 140,
Issue. ,
p.
100918.
Li, Cruz Y.
Chen, Zengshun
Weerasuriya, Asiri Umenga
Zhang, Xuelin
Lin, Xisheng
Zhou, Lei
Fu, Yunfei
and
Tse, Tim K.T.
2023.
Best practice guidelines for the dynamic mode decomposition from a wind engineering perspective.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 241,
Issue. ,
p.
105506.
Di Fiore, Francesco
Berri, Pier Carlo C.
and
Mainini, Laura
2023.
Rapid Assessment of Incipient Multimodal Faults of Complex Aerospace Systems.
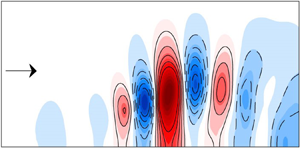
 $Re_c = 0.9\times 10^5$,
$Re_c = 0.9\times 10^5$,  $Re_c = 1\times 10^5$,
$Re_c = 1\times 10^5$,  $Re_c = 1.1\times 10^5$ and
$Re_c = 1.1\times 10^5$ and  $Re_c = 1.25\times 10^5$. All controlled cases exhibit a significant reduction in mean separation bubble height, requiring approximately 10 characteristic time periods to establish control.
$Re_c = 1.25\times 10^5$. All controlled cases exhibit a significant reduction in mean separation bubble height, requiring approximately 10 characteristic time periods to establish control.