Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T13:50:09.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Accurate solution method for the Maxey–Riley equation, and the effects of Basset history

Published online by Cambridge University Press:  11 April 2019

S. Ganga Prasath ,
Vishal Vasan Open the ORCID record for Vishal Vasan [Opens in a new window]  and
Rama Govindarajan
S. Ganga Prasath
Affiliation:
International Centre for Theoretical Sciences (ICTS-TIFR) Shivakote, Hesaraghatta Hobli, Bengaluru 560089, India
Vishal Vasan*
Affiliation:
International Centre for Theoretical Sciences (ICTS-TIFR) Shivakote, Hesaraghatta Hobli, Bengaluru 560089, India
Rama Govindarajan
Affiliation:
International Centre for Theoretical Sciences (ICTS-TIFR) Shivakote, Hesaraghatta Hobli, Bengaluru 560089, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Maxey–Riley equation has been extensively used by the fluid dynamics community to study the dynamics of small inertial particles in fluid flow. However, most often, the Basset history force in this equation is neglected. Analytical solutions have almost never been attempted because of the difficulty in handling an integro-differential equation of this type. Including the Basset force in numerical solutions of particulate flows involves storage requirements which rapidly increase in time. Thus the significance of the Basset history force in the dynamics has not been understood. In this paper, we show that the Maxey–Riley equation in its entirety can be exactly mapped as a forced, time-dependent Robin boundary condition of the one-dimensional diffusion equation, and solved using the unified transform method. We obtain the exact solution for a general homogeneous time-dependent flow field, and apply it to a range of physically relevant situations. In a particle coming to a halt in a quiescent environment, the Basset history force speeds up the decay as a stretched exponential at short time while slowing it down to a power-law relaxation, 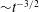${\sim}t^{-3/2}$, at long time. A particle settling under gravity is shown to relax even more slowly to its terminal velocity (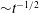${\sim}t^{-1/2}$), whereas this relaxation would be expected to take place exponentially fast if the history term were to be neglected. An important mechanism for the growth of raindrops is by the gravitational settling of larger drops through an environment of smaller droplets, and repeatedly colliding and coalescing with them. Using our solution we estimate that the rate of growth rate of a raindrop can be grossly overestimated when history effects are not accounted for. We solve exactly for particle motion in a plane Couette flow and show that the location (and final velocity) to which a particle relaxes is different from that due to Stokes drag alone. For a general flow, our approach makes possible a numerical scheme for arbitrary but smooth flows without increasing memory demands and with spectral accuracy. We use our numerical scheme to solve an example spatially varying flow of inertial particles in the vicinity of a point vortex. We show that the critical radius for caustics formation shrinks slightly due to history effects. Our scheme opens up a method for future studies to include the Basset history term in their calculations to spectral accuracy, without astronomical storage costs. Moreover, our results indicate that the Basset history can affect dynamics significantly.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Low-Reynolds-number flows: Stokesian dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 868 , 10 June 2019 , pp. 428 - 460
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ablowitz, M. J. & Fokas, A. S. 2003 Complex Variables: Introduction and Applications. Cambridge University Press.Google Scholar
Ardekani, M. N., Sardina, G., Brandt, L., Karp-Boss, L., Bearon, R. N. & Variano, E. A. 2017 Sedimentation of elongated non-motile prolate spheroids in homogenous isotropic turbulence. J. Fluid Mech. 831, 655–674.Google Scholar
Balachandar, S. 2009 A scaling analysis for point–particle approaches to turbulent multiphase flows. Intl J. Multiphase Flow 35 (9), 801–810.Google Scholar
Basset, A. B. 1888 A Treatise on Hydrodynamics: with Numerous Examples, vol. 2. Bell.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 2005 Bubbles, Drops, and Particles. Courier Corporation.Google Scholar
Daitche, A. 2013 Advection of inertial particles in the presence of the history force: higher order numerical schemes. J. Comput. Phys. 254, 93–106.Google Scholar
Daitche, A. 2015 On the role of the history force for inertial particles in turbulence. J. Fluid Mech. 782, 567–593.Google Scholar
Daitche, A. & Tél, T. 2011 Memory effects are relevant for chaotic advection of inertial particles. Phys. Rev. Lett. 107 (24), 244501.Google Scholar
Daitche, A. & Tél, T. 2014 Memory effects in chaotic advection of inertial particles. New J. Phys. 16 (7), 073008.Google Scholar
Deconinck, B., Guo, Q., Shlizerman, E. & Vasan, V. 2018 Fokas’s unified transform method for linear systems. Q. Appl. Maths 76, 463–488.Google Scholar
Deconinck, B., Trogdon, T. & Vasan, V. 2014 The method of Fokas for solving linear partial differential equations. SIAM Rev. 56 (1), 159–186.Google Scholar
Deepu, P., Ravichandran, S. & Govindarajan, R. 2017 Caustics-induced coalescence of small droplets near a vortex. Phys. Rev. Fluids 2 (2), 024305.Google Scholar
Elghannay, H. A. & Tafti, D. K. 2016 Development and validation of a reduced order history force model. Intl J. Multiphase Flow 85, 284–297.Google Scholar
Falkovich, G., Fouxon, A. & Stepanov, M. G. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419 (6903), 151.Google Scholar
Farazmand, M. & Haller, G. 2015 The Maxey–Riley equation: existence, uniqueness and regularity of solutions. Nonlinear Anal. Real World Applics 22, 98–106.Google Scholar
Fokas, A. S. 2008 A Unified Approach to Boundary Value Problems, CBMS-NSF Regional Conference Series in Applied Mathematics. SIAM.Google Scholar
Govindarajan, R. & Ravichandran, S. 2017 Cloud microatlas. Resonance 22 (3), 269–277.Google Scholar
Guseva, K., Daitche, A., Feudel, U. & Tél, T. 2016 History effects in the sedimentation of light aerosols in turbulence: the case of marine snow. Phys. Rev. Fluids 1 (7), 074203.10.1103/PhysRevFluids.1.074203Google Scholar
Guseva, K., Daitche, A. & Tél, T. 2017 A snapshot attractor view of the advection of inertial particles in the presence of history force. Eur. Phys. J., Spec. Top. 226 (9), 2069–2078.Google Scholar
Klinkenberg, J., de Lange, H. C. & Brandt, L. 2014 Linear stability of particle laden flows: the influence of added mass, fluid acceleration and Basset history force. Meccanica 49 (4), 811–827.Google Scholar
Langlois, G. P., Farazmand, M. & Haller, G. 2015 Asymptotic dynamics of inertial particles with memory. J. Nonlinear Sci. 25 (6), 1225–1255.Google Scholar
Ling, Y., Parmar, M. & Balachandar, S. 2013 A scaling analysis of added-mass and history forces and their coupling in dispersed multiphase flows. Intl J. Multiphase Flow 57, 102–114.Google Scholar
Lovalenti, P. M. & Brady, J. F. 1993a The force on a sphere in a uniform flow with small-amplitude oscillations at finite Reynolds number. J. Fluid Mech. 256, 607–614.Google Scholar
Lovalenti, P. M. & Brady, J. F. 1993b The hydrodynamic force on a rigid particle undergoing arbitrary time-dependent motion at small Reynolds number. J. Fluid Mech. 256, 561–605.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Mei, R. & Adrian, R. J. 1992 Flow past a sphere with an oscillation in the free-stream velocity and unsteady drag at finite Reynolds number. J. Fluid Mech. 237, 323–341.Google Scholar
Miller, P. D. 2006 Applied Asymptotic Analysis, vol. 75. American Mathematical Society.Google Scholar
Olivieri, S., Picano, F., Sardina, G., Iudicone, D. & Brandt, L. 2014 The effect of the Basset history force on particle clustering in homogeneous and isotropic turbulence. Phys. Fluids 26 (4), 041704.Google Scholar
Parmar, M., Annamalai, S., Balachandar, S. & Prosperetti, A. 2018 Differential formulation of the viscous history force on a particle for efficient and accurate computation. J. Fluid Mech. 844, 970–993.Google Scholar
Ravichandran, S. & Govindarajan, R. 2015 Caustics and clustering in the vicinity of a vortex. Phys. Fluids 27 (3), 033305.Google Scholar
Ravichandran, S. & Govindarajan, R. 2017 Vortex-dipole collapse induced by droplet inertia and phase change. J. Fluid Mech. 832, 745–776.Google Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Van Hinsberg, M. A. T., ten Thije Boonkkamp, J. H. M. & Clercx, H. J. 2011 An efficient, second order method for the approximation of the Basset history force. J. Comput. Phys. 230 (4), 1465–1478.Google Scholar