No CrossRef data available.
Published online by Cambridge University Press: 12 December 2023
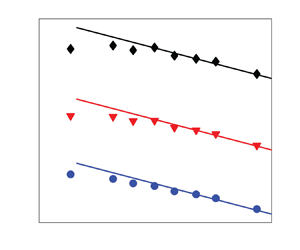
The effect of a uniform mean scalar gradient on the small scales of a passive scalar field in statistically stationary homogeneous isotropic turbulence is investigated through the transport equation for the scalar fluctuation. After some manipulation of the equation, it is shown that the effect can be recast in the form  $S_\theta ^* {{Pe^{-1}_{\lambda _\theta }}}$ (
$S_\theta ^* {{Pe^{-1}_{\lambda _\theta }}}$ ( $S_\theta ^*$ is the non-dimensional scalar gradient,
$S_\theta ^*$ is the non-dimensional scalar gradient,  ${{Pe_{\lambda _\theta }}}$ is the turbulent Péclet number). This effect gradually disappears as
${{Pe_{\lambda _\theta }}}$ is the turbulent Péclet number). This effect gradually disappears as  ${{Pe_{\lambda _\theta }}}$ becomes sufficiently large, implying a gradual approach towards local isotropy of the passive scalar. It is further argued that, for a given
${{Pe_{\lambda _\theta }}}$ becomes sufficiently large, implying a gradual approach towards local isotropy of the passive scalar. It is further argued that, for a given  $S_\theta ^*$, the normalized odd moments of the scalar derivative tend towards isotropy as
$S_\theta ^*$, the normalized odd moments of the scalar derivative tend towards isotropy as  ${{Pe^{-1}_{\lambda _\theta }}}$. This is supported by direct numerical simulations data for the normalized odd moments of the scalar derivative at large Péclet numbers. Further, the present derivation leads to the same prediction (
${{Pe^{-1}_{\lambda _\theta }}}$. This is supported by direct numerical simulations data for the normalized odd moments of the scalar derivative at large Péclet numbers. Further, the present derivation leads to the same prediction ( ${\sim }Sc^{-0.45}$ where Sc is the Schmidt number) as Buaria et al. (Phys. Rev. Lett., vol. 126, no. 3, 2021a, p. 034504) and complements the derivation by the latter authors, which is based on dimensional arguments and the introduction of a new diffusive length scale.
${\sim }Sc^{-0.45}$ where Sc is the Schmidt number) as Buaria et al. (Phys. Rev. Lett., vol. 126, no. 3, 2021a, p. 034504) and complements the derivation by the latter authors, which is based on dimensional arguments and the introduction of a new diffusive length scale.