Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1975.
Stochastic Optimization Models in Finance.
p.
701.
Cover, T.
1984.
An algorithm for maximizing expected log investment return.
IEEE Transactions on Information Theory,
Vol. 30,
Issue. 2,
p.
369.
Tibiletti, Luisa
1994.
Operations Research Models in Quantitative Finance.
p.
172.
Board, John L. G.
Sutcliffe, Charles M. S.
and
Ziemba, William T.
2001.
Encyclopedia of Optimization.
p.
1794.
Sakalauskas, L.
2006.
Coping with Uncertainty.
Vol. 581,
Issue. ,
p.
257.
Board, John L.G.
Sutcliffe, Charles M.S.
and
Ziemba, William T.
2008.
Encyclopedia of Optimization.
p.
2696.
Estrada, Javier
2009.
Geometric Mean Maximization: An Overlooked Portfolio Approach?.
SSRN Electronic Journal,
Estrada, Javier
2010.
Geometric Mean Maximization: An Overlooked Portfolio Approach?.
The Journal of Investing,
Vol. 19,
Issue. 4,
p.
134.
Weide, James H. Vander
2010.
Handbook of Portfolio Construction.
p.
153.
De Santiago, Rafael
and
Estrada, Javier
2011.
Geometric Mean Maximization: Expected, Observed, and Simulated Performance.
SSRN Electronic Journal,
Zhang, Guoyi
2012.
Optimal Geometric Mean Returns of Stocks and Their Options.
International Journal of Stochastic Analysis,
Vol. 2012,
Issue. ,
p.
1.
Santiago, Rafael De
and
Estrada, Javier
2013.
Geometric Mean Maximization:Expected, Observed,and Simulated Performance.
The Journal of Investing,
p.
130518050207001.
Santiago, Rafael De
and
Estrada, Javier
2013.
Geometric Mean Maximization: Expected, Observed,and Simulated Performance.
The Journal of Investing,
Vol. 22,
Issue. 2,
p.
109.
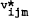 , may be found by maximizing
, may be found by maximizing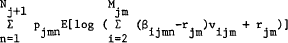

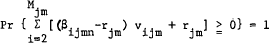 ,
,