2. The financial market model

Consider a corporation in a competitive economy operating between the dates t = 0 and 1. The dates t = 0 and 1 are subsequently referred to as now and then, respectively. Decisions are made now, and payoffs on those decisions are received then. The economy is composed of corporations and risk-averse investors. Investors make portfolio decisions to maximize their expected utility subject to a budget constraint.Footnote ⁷ The corporation of interest here is a firm operating in a market for goods and services, making an investment decision and managing its corporate pension plan.

The firm is assumed to operate in competitive markets and makes investment decisions to advance its operations. The firm also has a pension plan for its employees that consists of an asset portfolio to cover the pension liabilities. Let Π (I,  ω) denote the random payoff then on the investment of I dollars now; suppose that the investment frontier Π is increasing and concave in the dollar investment. Let A and L denote the asset and liability values then for the pension fund. Suppose the asset and liability values increase in state.Footnote ⁸

The firm also faces common capital market risks such as interest rate and insolvency risks in addition to the longevity risk on its pension plan. The returns on its pension asset portfolio payoff then, and the liability portfolio is composed of the pension payouts made then. The following partially summarizes the notation used in the development of the model:

The corporation is managed by an individual who makes decisions now. This individual will be referred to as the chief executive officer (CEO). The CEO makes the same decisions that other investors make and, in addition, makes decisions on behalf of the corporation. To distinguish between the two sets of decisions, the investor decisions on a portfolio are called decisions on personal account while the CEO decisions on investment, financing, and risk management are called decisions on corporate account. The CEO, like the investors, has an increasing concave utility function that expresses preferences for consumption now and then. The CEO makes decisions to maximize expected utility subject to a budget constraint and the corporate financing constraint. All decisions on personal and corporate account are made now, and the payoffs on those decisions occur then. We assume that the CEO is paid in salary and stock; it follows that the CEO makes decisions on corporate account to maximize the current shareholder value subject to any financing constraint.Footnote ¹⁰

3. The unhedged firm

Suppose the financial markets are competitive. In the absence of any hedge and letting b denote the promised payment on debt issued to finance the firm's capital investment, the stock market value of the firm may be expressed as:Footnote ¹¹

(1)$$S^u = \int_0^\zeta {max\{ {0, \;\Pi + A-L-b} \} } dP$$

where max{0, Π + A − L − b} is the firm's payoff in the absence of any hedging instrument.

3.1 No insolvency risk

First, consider the firm with no insolvency risk due to its investment decisions or pension plan. Suppose the firm finances any investment decision with debt. No insolvency provides a base case in which the firm makes decisions in the interests of all the stakeholders, i.e., stockholders, bondholders, and pension holders. The stock value in this case is

(2)$$S^u = \int_0^\zeta {( {\Pi + A-L-b} ) } dP$$

The stock value may also be expressed as

(3)$$\eqalign{S^u& = \int_0^\zeta \Pi dP + \int_0^\zeta {( {A-L} ) } dP-\int_0^\zeta b \,dP \cr & = V^{\rm e} + \Delta -B( b) } $$

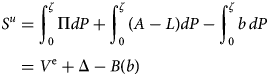
where V is the corporate value, Δ is the over or underfunding of the pension plan, and B(b) is the value of the safe debt issue used to finance the firm's investment decision. The firm's constrained maximization problem is

(4)$$\eqalign{& maximize\,S^u( 1) \cr & subject\,to\,B( b) = I} $$

The Lagrange function is

$$L( {I, \;b, \;\lambda } ) = S^u( I) + \lambda ( B( b) -I) $$

and we have the following first order conditions:

(5)$$D_1L = \int_0^\zeta {D_1\Pi dP-\lambda = 0} $$

(6)$$D_2L = {-}\int_0^\zeta {dP + \lambda } \int_0^\zeta {dP = 0} $$

(7)$$D_3L = B( b) -I = 0$$

It follows by (6) and (5), that the optimal investment is the socially efficient level I ^e implicitly defined by

(8)$$\int_0^\zeta {D_1\Pi ( I^e, \;\omega ) dP( \omega ) -1 = 0} $$

The investment I ^e maximizes the stock value of the corporation without changing the value of the debt or pension plan. Given the financing constraint in (4), it follows that the stock market value of the firm may also be expressed as

(9)$$\eqalign{S^u& = V^e-B( b) + \Delta \cr & = npv( {I^e} ) + \Delta } $$

where npv is the risk-adjusted net present value of the investment I ^e. This investment maximizes the npv while Δ is the over or underfunding of the pension plan; if the plan is underfunded, then the firm invests if and only if the net present value covers the underfunding and provides a return for shareholders.

3.2 Insolvency risk

From the firm's perspective, the pension plan exposes the corporation to the risk that the pensioners live longer than expected, and so we refer to it as longevity risk. The longevity risk may yield insolvency risk if the pension asset portfolio and corporate payoff are insufficient to cover the pension liability.

To note the pension and insolvency risk it is instructive to rewrite the stock value. Observe that max{0,  Π + A − L − b} = Π + A − L − b + max{0,  L + b − (Π + A)} and so the stock value may also be expressed as follows:

(10)$$\eqalign{S^u& = \int_0^\zeta {( {\Pi + A-L-b} ) dP \;+ } \int_0^\zeta {max\{ {0, \;L + b-( {\Pi + A} ) } \} } dP \cr & = V + V_A-V_L-B( b) + ( {P^b + P^u} ) } $$

where V is the corporate value, V _A and V _L are pension asset and liability portfolio values and (P ^b + P ^u) is the put option value.Footnote ¹² Letting γ be implicitly defined by the condition Π(I,  γ) + A(γ) − L(γ) = 0 and δ is implicitly defined by the condition Π(I,  δ) + A(δ) − L(δ) − b = 0, these values are

$$V_A = \int_0^\zeta {A\,} dP\,and\,V_L = \int_0^\zeta L \,dP$$

and

$$\eqalign{P^b + P^u& = \int_0^\delta {( {L + b-( {\Pi + A} ) } ) dP} \cr & = \left({\int_0^\gamma {( {L + b-L} ) dP + \int_\gamma^\delta {( {L + b-( {\Pi + A} ) } ) } } dP} \right)\cr & \quad + \int_0^\gamma {( {L-( {\Pi + A} ) } ) } dP} $$

The pension liability value and put option values are shown in Figures 1 and 2. Given insolvency risk, the firm puts P ^b to bondholders and P ^u to the pension holders.

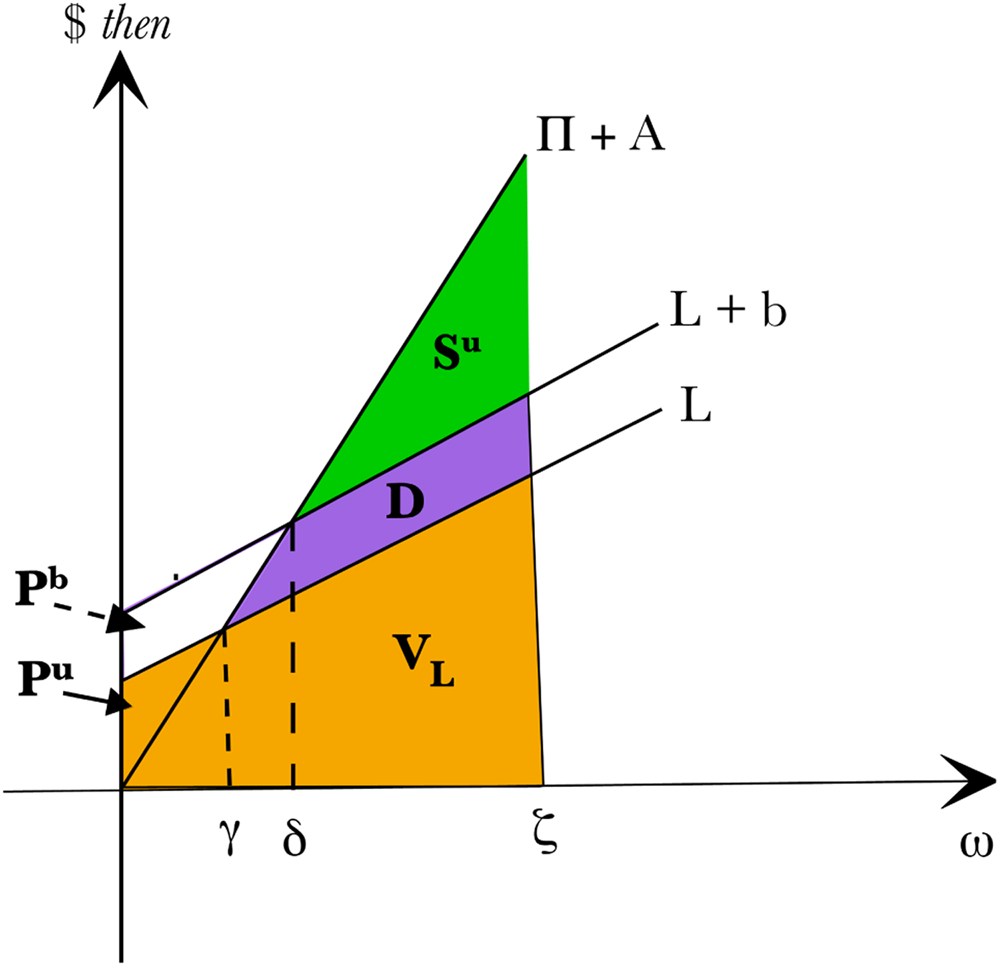
Figure 1. The Unhedged Firm.

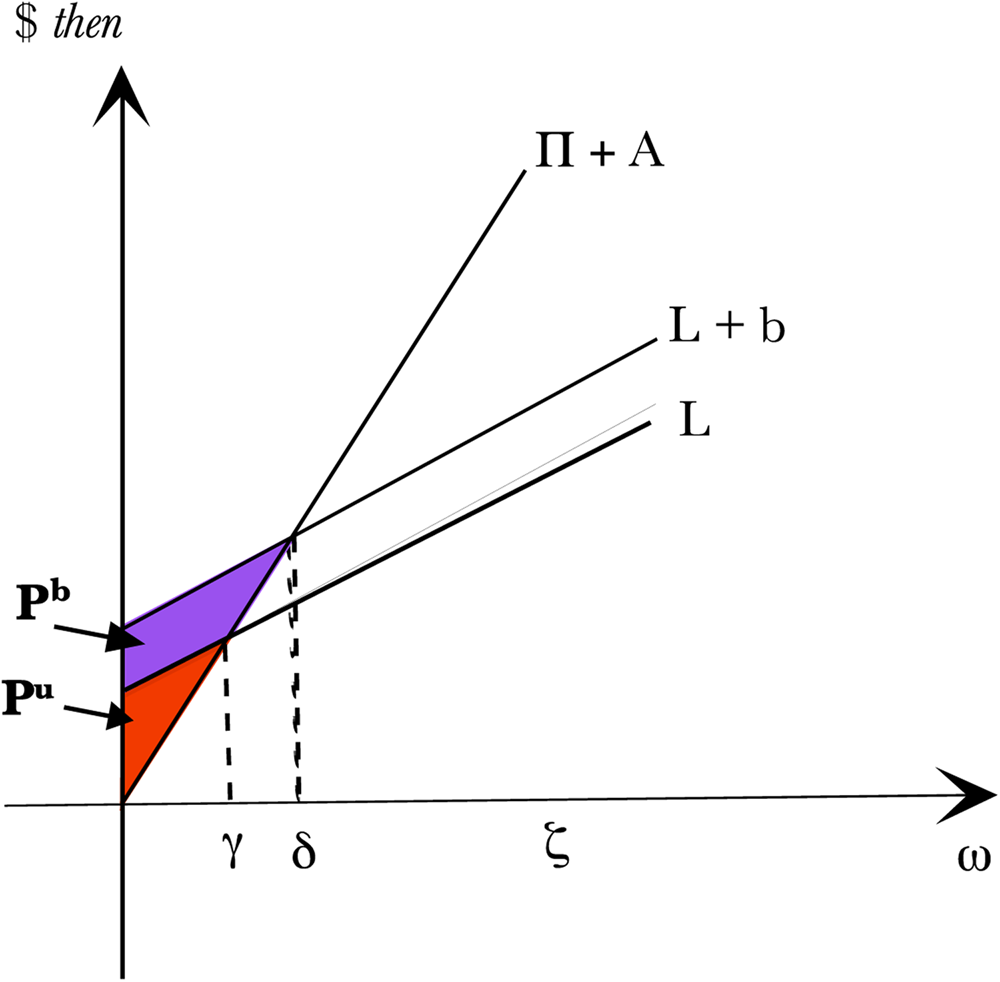
Figure 2. The Option Values.

If there is an implicit or explicit guarantee by the government, then the difference is put to the government rather than the annuity holders.

Now consider the investment decision made by the corporate manager. Given appropriately aligned incentives, the manager will select the investment to maximize the stock value subject to a financing constraint.Footnote ¹³ Without loss of generality, suppose the firm issues debt to cover the investment expenditure; let D(b) denote the value of the debt, and b represent the promised payment then. The manager's constrained maximization problem is

$$\eqalign{& maximize\,S^u \cr & subject\,to\,D( b) = I} $$

where

(11)$$S^u = \int_\delta ^\zeta {( {\Pi + A-L-b} ) dP} $$

and

(12)$$D( b ) = \int_\gamma ^\delta {( {\Pi + A-L} ) } dP + \int_\delta ^\zeta b \,dP$$

Let L(I,  b,  λ) = S ^u + λ(D(b) − I) be the Lagrange function for the constrained maximization problem. Then the first order conditions are as follows:

(13)$$D_1L = \int_\delta ^\varsigma {D_1\Pi \,dP + \lambda \left({\int_\gamma^\delta {D_1\Pi \,dP-1} } \right) = 0} $$

(14)$$D_2L = {-}\int_\delta ^\zeta {dP + \lambda \int_\delta ^\zeta {dP} = 0} $$

(15)$$D_3L = D( b ) -I = 0$$

Let I ^u denote the optimal investment decision for the manager. Note that by (14), the Lagrange multiplier is one, and so the first-order condition for the optimal investment is

(16)$$D_1L = \int_\gamma ^\zeta {D_1} \Pi dP-1 = 0.$$

It is useful to compare the investment decision with the same decision made in the absence of insolvency risk. Let I ^e denote that decision and call it the socially efficient investment; the socially efficient decision is made in the interests of all stakeholders in the corporation rather than just the stockholders. The socially efficient investment will satisfy the following condition:

(17)$$\int_0^\zeta {D_1\Pi dP-1 = \int_0^\gamma {D_1\Pi dP + \int_\gamma ^\zeta {D_1\Pi dP-1 = 0} } } $$

(8) implicitly defines the socially efficient investment. If (17) is evaluated at the optimal investment level for the unhedged firm, i.e., I ^u, then the first term on the right-hand side of (17) remains and makes (17) positive; it follows by the second-order condition that the manager selects I ^u < I ^e. Therefore, the unhedged firm underinvests relative to the socially efficient level of investment. The stock market value of the unhedged firm may also be written as follows:

(18)$$\eqalign{S^u& = V + V_A-V_L-B( b ) + ( {P^b + P^u} ) \cr & = V-( {B( b ) -P^b} ) + \Delta + P^u \cr & = V-D( b ) + \Delta + P^u \cr & = V-I + \Delta + P^u \cr & = npv( I ) + \Delta + P^u} $$

Given insolvency risk due to the pension fund and debt liabilities, the CEO only makes the capital investment decision if the risk-adjusted net present value exceeds any underfunding plus the pension put value.

It is also possible to obtain the value of the pension fund for the unhedged firm. If the value of the pension asset portfolio is less than the liability value, then the pension plan is underfunded, and Δ is negative. The value of the pension fund is then F ^u = V _L − P ^u.

4. The buy-in

The liability claims in the pension plan are one source of the insolvency risk for the firm. This risk becomes more of a problem for the firm as longevity increases. The firm can absorb the risk or chose to manage it in some way. Buy-in and buy-out instruments represent a growing segment of the markets for longevity risk transfer. The buy-in is considered first.

A buy-in is a transaction with an insurer in which the firm purchases an annuity that pays the pension claims as they are realized. Without loss of generality, we will suppose that the firm uses debt to finance the annuity purchase from an insurer. Then the constraint in the constrained maximization problem becomes

$$D( b ) = I + \int_0^\zeta {L\,} dP$$

Hence, a debt instrument replaces the pension liability as well as providing funds for the capital investment. The stock value for the buy-in becomes

$$S^i = \int_\gamma ^\zeta {( {\Pi + A-L-b + L} ) dP = \int_\gamma ^\zeta {( {\Pi + A-b} ) dP} } $$

where S ⁱ denotes the hedged corporate equity value (Figure 3). Similarly, let I ⁱ denote the stock value maximizing investment decision. The Lagrange function is

$$L^i( {I, \;b, \;\lambda } ) = S^i + \lambda \left({D( b ) -I-\int_0^\zeta L \,dP} \right)$$

and the first order conditions are as follows:

(19)$$D_1L^i = \int_\gamma ^\zeta {D_1\Pi dP-\lambda } \left({\int_0^\gamma {D_1\Pi dP-1} } \right) = 0$$

(20)$$D_2L^i = {-}\int_\gamma ^\zeta {dP + \lambda } \int_\gamma ^\zeta {dP} = 0$$

(21)$$D_3L^i = D( b ) -I-V_L = 0$$

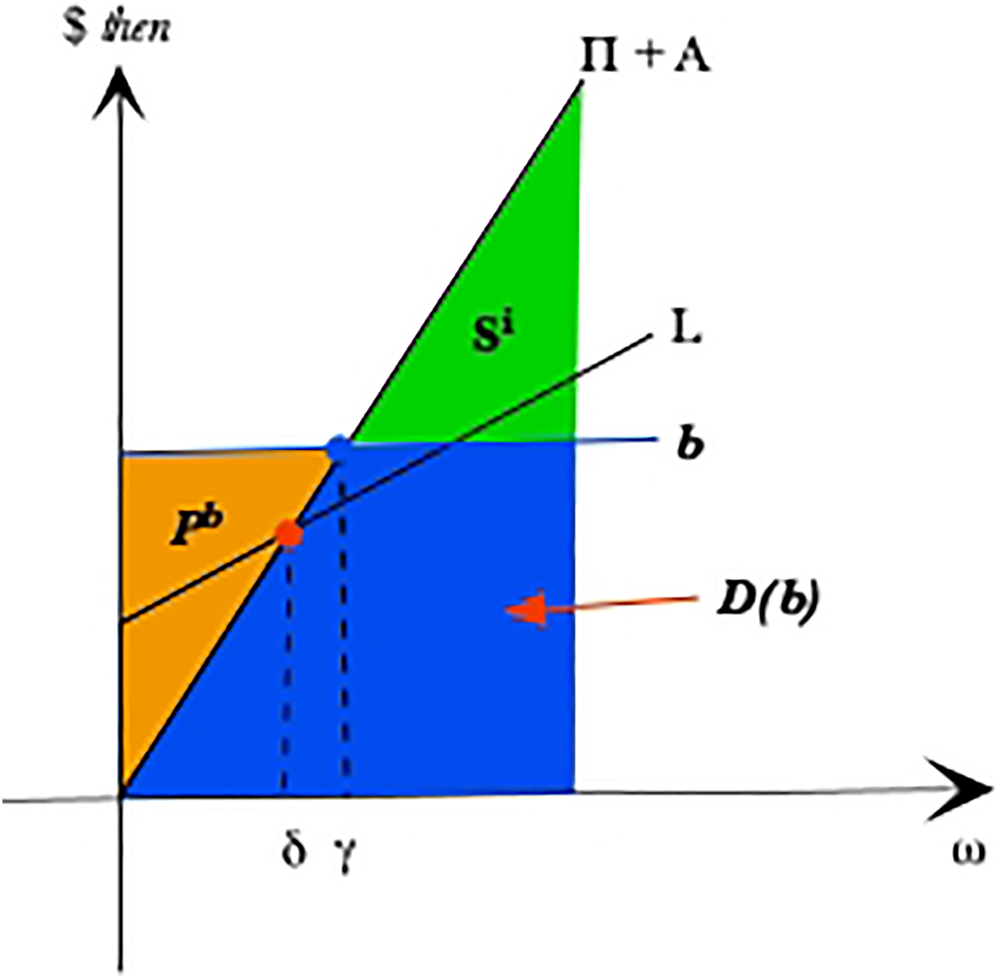
Figure 3. The Hedged Firm.

From (20) and (19) it follows that I ⁱ = I ^e > I ^u and so the buy-in resolves the under-investment problem. This under-investment problem is similar to that noted by Myers (Reference Myers1977); also, see Mayers and Smith (Reference Mayers and Smith1987), Garven and MacMinn (Reference Garven and MacMinn1993), MacMinn and Garven (Reference MacMinn, Garven and Dionne2011) for insurance schemes designed to alleviate the under-investment. Also, see Jensen and Meckling (Reference Jensen and Meckling1976), Green (Reference Green1984), MacMinn (Reference MacMinn1993) and MacMinn (Reference MacMinn2005b) for earlier examples of the agency costs of publicly traded firms and the impact of those costs on production, investment and financing decisions.

The shareholder value may also be expressed as

(22)$$\eqalign{S^i& = \int_0^\zeta {( {\Pi + A-b} ) dP + \int_0^\zeta {max\{ {0, \;b-( {\Pi + A} ) } \} dP} } \cr & = V + V_A-( {B( b ) -P^i} ) \cr & = V + V_A-D( b ) \cr & = V + V_A-( {V_L + I^i} ) \cr & = V-I^i + V_A-V_L \cr & = npv( {I^i} ) + \Delta } $$

where B(b) is the safe debt value and P ⁱ is the put option value, npv is the risk-adjusted net present value of the investment and Δ = V _A − V _L is the under or over funding of the pension plan. The difference in stock value between the unhedged and hedged firms is

(23)$$\eqalign{S^i-S^u& = npv( {I^i} ) + \Delta -( {npv( {I^u} ) + \Delta + P^u} ) \cr & = npv( {I^i} ) -npv( {I^u} ) -P^u} $$

Using (23), it may be noted that if the CEO managed the firm's longevity risk with a buy-in but maintained the same investment level at I ^u then the difference in stock value would be −P ^u since the buy-in would eliminate that put option value. Hence, the CEO acting in the interests of current shareholders would not transfer the longevity risk with a buy-in.

The CEO, however, has the ability to make a capital investment on behalf of the firm. Equation (22) shows that the CEO making the investment decision to maximize current shareholder value will equivalently make the corporate investment decision to maximize the risk adjusted net present value of the project. It follows, using (23), that the CEO will make the socially efficient investment decision and complete the buy-in if the increase in risk-adjusted net present value exceeds the loss in pension option value.

5. The buy-out

Consider a buy-out. In this case, the pension plan is transferred to another firm, e.g., insurer or reinsurer. The pension asset and liability portfolios that compose the plan are transferred. Suppose further that the pension plan is under-funded in the sense that the value of the asset portfolio is less than that of the liability portfolio, i.e.,

$$\int_0^\zeta {( {A-L} ) dP = \Delta } $$

In the under-funded case, Δ is negative, and the firm must raise −Δ dollars as part of the payment for the buy-out. The buy-out consists of this payment plus the transfer of the pension plan portfolios. The corporate payoff was Π + A − L before the buy-out while it is Π − b after the buy-out, where b is the promised payment on a bond issue needed to raise the −Δ dollars plus any investment expenditure. The constrained maximization problem for the firm in planning the buy-out and investment is

$$\eqalign{& maximize\,S^o( I ) \cr & subject\,to\,D( b ) = {-}\Delta + I} $$

where

(24)$$\eqalign{S^o& = \int_\delta ^\zeta {( {\Pi -b} ) dP} \cr D( b ) & = \int_0^\delta {( {\Pi + A} ) dP + \int_0^\zeta b } \,dP} $$

Letting the Lagrange function in this case be L(I,  b,  λ) = S ^o + λ(D + Δ − I). Then

(25)$$D_1L = \int_\delta ^\zeta {D_1\Pi \,dP + \lambda \left({\int_0^{^\delta } {D_1\Pi \,dP-1} } \right) = 0} $$

(26)$$D_2L = {-}\int_\delta ^\zeta {dP + \lambda \int_\delta ^\zeta {dP} = 0} $$

(27)$$D_3L = D( b ) + \Delta -I = 0$$

From (26) it follows that λ = 1 and so by (25) it follows that

$$D_1L = \int_0^\zeta {D_1\Pi \,} dP-1 = 0$$

Therefore, the investment level that maximizes this constrained maximization problem is I ^o which is implicitly defined by (25). It also follows then that I ^o = I ⁱ = I ^e. The buy-out solves the under-investment problem just as the buy-in does.

Next, recall that the stock value of the firm after the buy-out is

(28)$$\eqalign{S^o& = \int_\delta ^\zeta {( {\Pi -b} ) dP} \cr & = \int_0^\zeta {max\{ {0, \;( {\Pi -b} ) } \} dP} \cr & = \int_0^\zeta {( {\Pi -b} ) dP + \int_0^\zeta {max\{ {0, \;b-\Pi } \} dP\,0} } \cr & = V-B( b ) + P^o \cr & = V-D( b ) \cr & = V + \Delta -I^o \cr & = npv( {I^o} ) + \Delta } $$

It may be noted that the net present value of the firm investment in the buy-in and buy-out cases is the same, and so the stock value of the firm will also be the same in each case.

6. Longevity bonds without basis risk

Finally, consider a longevity bond. Let B(ω) be the longevity bond payoff then in state ω. Suppose there is no basis risk so that the bond payoff matches the pension claims then, i.e., B(ω) = L(ω) for each state ω ∈ Ω. If the corporation hedges the longevity risk with a longevity bond, the corporate payoff becomes Π + A − L + B − b = Π + A − b. Without loss of generality, suppose the corporation raises the money for investment and the longevity bond with a debt issue. Then the financing constraint is

$$D( b ) = I + \int_0^\zeta B ( \omega ) dP( \omega ) $$

where the debt value is

$$D( b ) = \int_0^\delta {( {\Pi + A} ) dP + \int_\delta ^\zeta b } \,dP$$

and the stock value given the longevity bond is

$$S^l = \int_\delta ^\zeta {( {\Pi + A-b} ) dP} $$

The Lagrange function for this constrained maximization problem is

$$L( {I, \;b, \;\lambda } ) = S^l( {I, \;b} ) + \lambda \left({D( b ) -I-\int_0^\zeta {B( \omega ) dP} } \right)$$

and the first order conditions are:

$$D_1L = \int_\delta ^\zeta {D_1} \Pi \,dP + \lambda \left({\int_0^\delta {D_1\Pi \,dP-1} } \right) = 0$$

$$D_2L = {-}\int_\delta ^\zeta {dP + \lambda } \,\int_\delta ^\zeta {dP} = 0$$

$$D_3L = D( b ) -I-\int_0^\zeta {BdP = 0} $$

It follows from these first order conditions that the optimal investment I ^l is implicitly defined by the condition:

$$\int_0^\zeta D _1\Pi \,dP = 1$$

and so, it also follows that the longevity bond hedge with no basis risk solves the under-investment problem and makes I ^l = I ^e > I ^u. It may be noted that the stock value of the corporation hedged with a longevity bond may be equivalently expressed as

$$\eqalign{S^l& = \int_0^\zeta {max\{ {0, \;\Pi + A-b} \} dP} \cr & = \int_0^\zeta {( {\Pi + {\rm A}-b} ) dP + \int_0^\zeta {max\{ {0, \;b-( {\Pi + A} ) } \} dP} } \cr & = V + V_A-B( b ) + P^b \cr & = V + V_A-D( b ) \cr & = V-I + V_A-V_L \cr & = npv + \Delta } $$

Hence the longevity bond with no basis risk solves the under-investment problem that exists for the unhedged firm and yields I ^l = I ^e > I ^u.

7. Longevity bond with basis risk

If there is basis risk, then the payoff on a longevity bond is tied to a longevity index that is not perfectly correlated with the longevity of the pension fund. The corporation will not be able to perfectly hedge the longevity risk of the pension fund. It may, however, be able to reduce the longevity risk and alleviate the under-investment problem.

Let the basis risk be denoted by L(ω) − L _I(ω). This represents the difference between the realized liability of the pension fund in a particular state versus the realized value of a longevity index where the index is based on a similar but not identical population. Suppose that longevity index over-estimates the pension fund liability then for lower states while the index under-estimates the pension fund liability then for higher states as shown in Figure 4. Let B ^l denote the risk adjusted market value of the longevity bond so that (Figure 5)

$$B^l = \int_0^\zeta {L_I( \omega ) } \,dP( \omega ) \equiv V_I$$

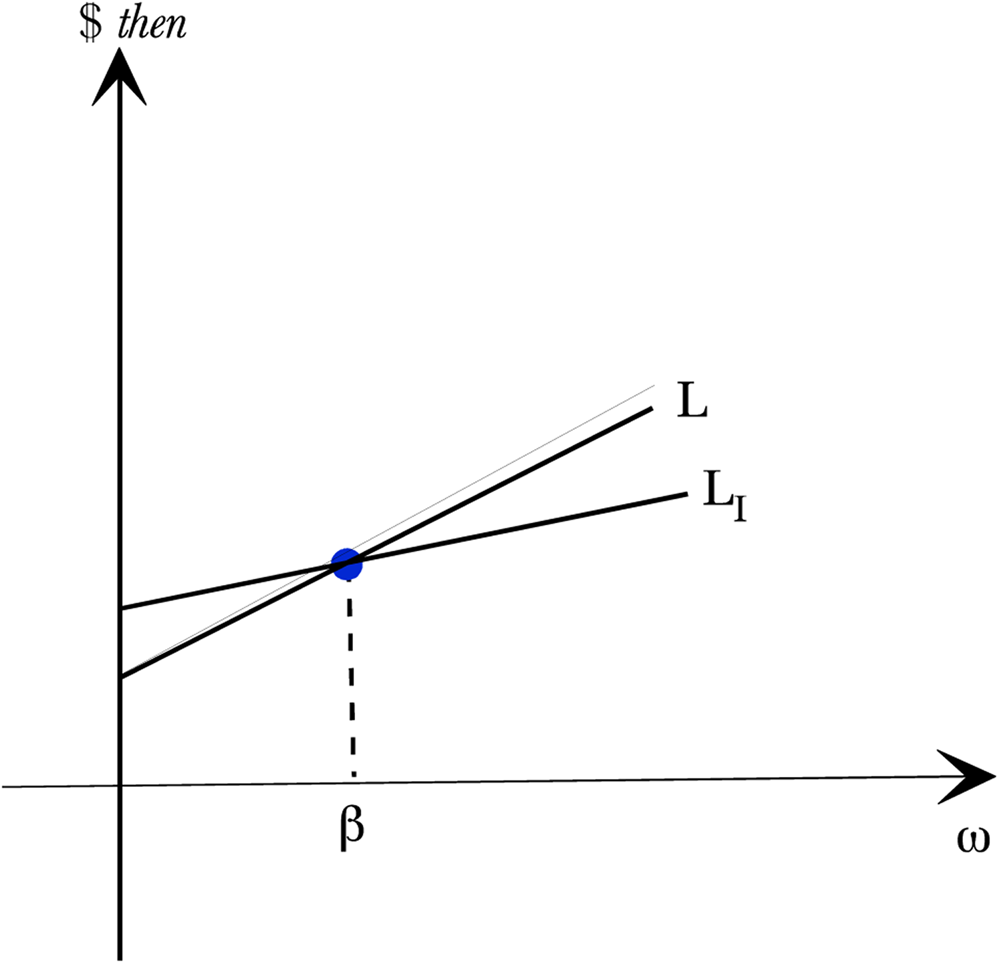
Figure 4. Basis Risk.

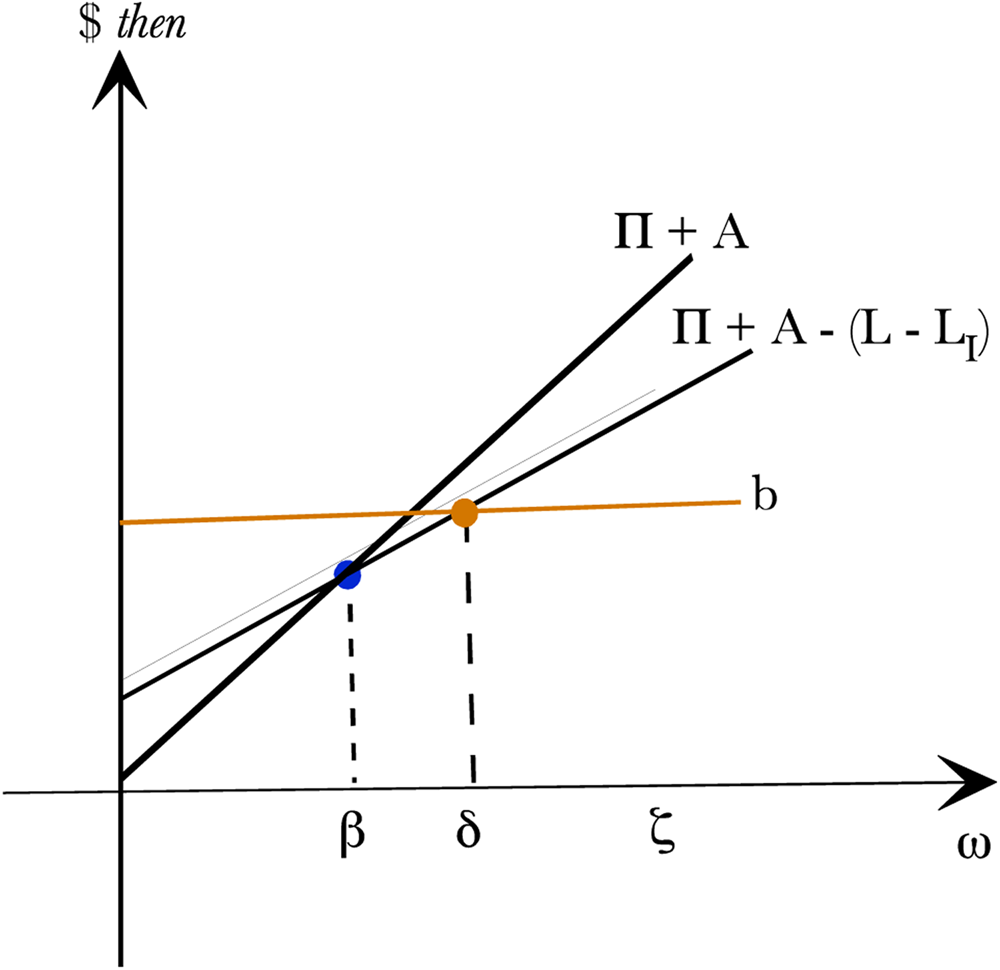
Figure 5. Corporate Payoff with Basis Risk.

If the corporation hedges with this longevity bond, then the shareholder payoff becomes

$$\eqalign{& max\{ {0, \;\Pi + A-( {L-L_I} ) -b} \} \cr & = \Pi + A-( {L-L_I} ) -b \cr & \quad\hskip 1pt+ max\{ {0, \;b-( {\Pi + A-( {L-L_I} ) } ) } \} } $$

and the stock market value of the hedged corporation with a longevity bond is

$$S^l = \int_\delta ^\zeta {( {\Pi + A-( {L-L_I} ) -b} ) dP} $$

and the bond value of a new issue is

$$D( b ) = \int_0^\delta {( {\Pi + A-( {L-L_I} ) } ) dP + \int_\delta ^\zeta {bdP} } $$

The constrained maximization problem becomes

$$\eqalign{& maximize\,S^l \cr & subject\,to\,D( b) = I + B^l} $$

The Lagrange function is

$$L( {I, \;b, \;\lambda } ) = S^l + \lambda ( {D( b ) -I-B^l} ) $$

and the first order conditions are as follows:

$$D_1L = \int_\delta ^\zeta {D_1\Pi } \,dP + \lambda \left({\int_0^\delta {D_1\Pi \,dP-1} } \right) = 0$$

$$D_2L = {-}\int_\delta ^\zeta {dP + \lambda \int_\delta ^\zeta {dP = 0} } $$

$$D_3L = D( b ) -I-\int_0^\zeta {BdP = 0} $$

As before the stock market value of the corporation hedging with the longevity bond is

$$\eqalign{S^l& = V + V_A-( {V_L-V_I} ) -B( b ) + P^b \cr & = V + V_A-( {V_L-V_I} ) -D( b ) \cr & = V + V_A-( {V_L-V_I} ) -( {I + V_I} ) \cr & = npv( {I^l} ) + \Delta } $$

where npv(I ^l) is the risk adjusted net present value of the investment I ^l = I ^e. The last equality follows by the financing constraint that makes the debt value equal to the investment expenditure plus the value of the indexed longevity bond. Here again, the longevity bond solves the under-investment problem and allows the firm to select the efficient investment level if the risk adjusted net present value of the efficient investment is greater than the net present value plus the put option value of the unhedged corporation. The basis risk introduces a costFootnote ¹⁴ but if the longevity bond hedges the insolvency risk, then the longevity bond will reduce or eliminate the under-investment problem.

8. Concluding remarks

The analysis here has shown that the buy-in and buy-out instruments purchased from insurers can be used to manage the longevity risk of the corporate pension plan. These instruments transfer the risk and increase the value of the pension plan, but ceteris paribus, such hedging was shown to reduce shareholder value. Furthermore, the analysis has shown that if the corporation has an investment opportunity but a pension plan that exposes it to insolvency risk, it faces an under-investment problem. The CEO invests to the point at which the marginal risk-adjusted present value of the investment equals one plus the marginal agency cost of the under-investment problem; the marginal agency cost is represented by the marginal loss in the put option value P ^u. Effective risk management instruments eliminate or reduce the marginal agency cost. The model introduced here is the first theoretical model to show that buy-ins and buy-outs eliminate the agency cost and so the under-investment.

The model predictions are supported by some empirical evidence. For example, the deals by GM and Verizon with Prudential in 2012. These two deals are two of the largest buy-out transactions to date. Prior to the pension buy-out announcement, GM shares had gone down by 3.4% as it released weaker-than-expected auto sales figures. However, the stock recouped its losses and rose as much as 5.1% on the news of the pension buy-out on June 1, 2012, i.e., see Seetharaman and Klayman (Reference Seetharaman and Klayman2012). Similarly, on October 17, 2012, Verizon shares closed at $44.72, up 1.5%, after it announced its buy-out deal with Prudential.Footnote ¹⁵ Also, consistent with the model's prediction, after the pension buy-outs, both companies increased their investments significantly.

The analysis also shows that a longevity bond with or without basis risk can be used to manage the longevity risk. With no basis risk, the results are equivalent to those of the buy-in and buy-out. With basis risk, the risk management becomes more difficult because the index used for the liability payoff does not perfectly match the actual liability; this, in turn, increases the cost of the risk management. Despite this cost, the analysis shows in a simple setting that an instrument with basis risk can be used to manage the longevity risk and eliminate the under-investment problem.

Here the longevity risk was the source of the insolvency risk and so the longevity linked financial instruments could be used to manage that risk. An expanded model in which there are more sources of insolvency risk will make the instruments considered here possibly less effective. Such a model while possibly showing that the longevity linked instruments cannot eliminate the agency cost associated with the under-investment problem may also show that those instruments will reduce the agency cost and that other hedging instruments used in conjunction with them can eliminate the agency cost.